Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.6 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( |x| + |y| = x + y \)
б) \( |x| + |y| = y — x \)
в) \( |x| + |y| = x — y \)
г) \( |x| + |y| = -x — y \)
Построить график уравнения
а) \( |x| + |y| = x + y \)
\( (|x| — x) + (|y| — y) = 0 \).
Первое слагаемое:
\( |x| — x ≥ 0 \);
\( |x| — x = 0 \);
\( |x| = x \);
\( x ≥ 0 \).
Второе слагаемое:
\( |y| — y ≥ 0 \);
\( |y| — y = 0 \);
\( |y| = y \);
\( y ≥ 0 \).
График уравнения:
б) \( |x| + |y| = y — x \)
\( (|x| + x) + (|y| — y) = 0 \).
Первое слагаемое:
\( |x| + x ≥ 0 \);
\( |x| + x = 0 \);
\( |x| = -x \);
\( x ≤ 0 \).
Второе слагаемое:
\( |y| — y ≥ 0 \);
\( |y| — y = 0 \);
\( |y| = y \);
\( y ≥ 0 \).
График уравнения:
в) \( |x| + |y| = x — y \)
\( (|x| — x) + (|y| + y) = 0 \).
Первое слагаемое:
\( |x| — x ≥ 0 \);
\( |x| — x = 0 \);
\( |x| = x \);
\( x ≥ 0 \).
Второе слагаемое:
\( |y| + y ≥ 0 \);
\( |y| + y = 0 \);
\( |y| = -y \);
\( y ≤ 0 \).
График уравнения:
г) \( |x| + |y| = -x — y \)
\( (|x| + x) + (|y| + y) = 0 \).
Первое слагаемое:
\( |x| + x ≥ 0 \);
\( |x| + x = 0 \);
\( |x| = -x \);
\( x ≤ 0 \).
Второе слагаемое:
\( |y| + y ≥ 0 \);
\( |y| + y = 0 \);
\( |y| = -y \);
\( y ≤ 0 \).
График уравнения:
а) \( |x| + |y| = x + y \)
Преобразуем уравнение:
\( (|x| — x) + (|y| — y) = 0 \).
Рассмотрим каждое слагаемое отдельно.
Первое слагаемое:
\( |x| — x ≥ 0 \).
Значение модуля \( |x| \) равно \( x \), если \( x ≥ 0 \), и равно \( -x \), если \( x < 0 \).
Для выполнения условия \( |x| — x = 0 \), необходимо:
\( |x| = x \).
Следовательно, \( x ≥ 0 \).
Второе слагаемое:
\( |y| — y ≥ 0 \).
Значение модуля \( |y| \) равно \( y \), если \( y ≥ 0 \), и равно \( -y \), если \( y < 0 \).
Для выполнения условия \( |y| — y = 0 \), необходимо:
\( |y| = y \).
Следовательно, \( y ≥ 0 \).
График уравнения:
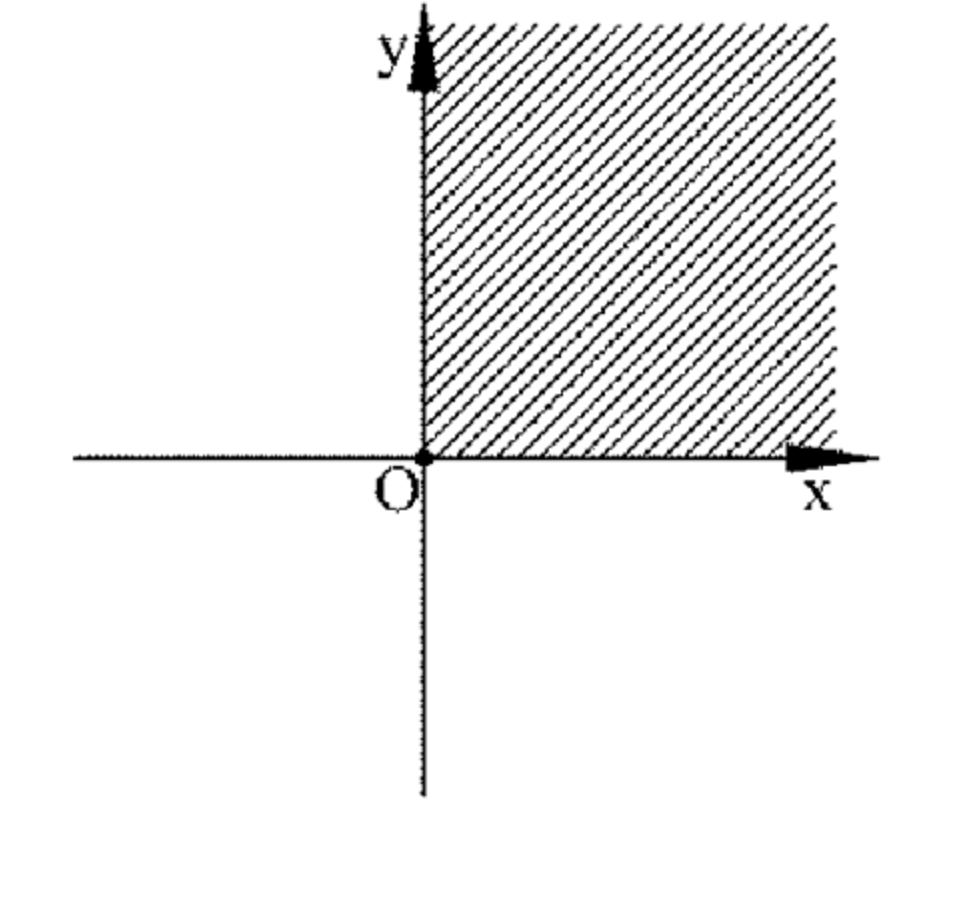
Уравнение \( |x| + |y| = x + y \) выполняется только в первой четверти координатной плоскости, где \( x ≥ 0 \) и \( y ≥ 0 \).
График представляет собой прямую линию, проходящую через точки:
— \( (0, 0) \);
— \( (1, 1) \);
— \( (2, 2) \).
Линия наклонена под углом \( 45^\circ \) к оси \( x \).
б) \( |x| + |y| = y — x \)
Преобразуем уравнение:
\( (|x| + x) + (|y| — y) = 0 \).
Рассмотрим каждое слагаемое отдельно.
Первое слагаемое:
\( |x| + x ≥ 0 \).
Значение модуля \( |x| \) равно \( x \), если \( x ≥ 0 \), и равно \( -x \), если \( x < 0 \).
Для выполнения условия \( |x| + x = 0 \), необходимо:
\( |x| = -x \).
Следовательно, \( x ≤ 0 \).
Второе слагаемое:
\( |y| — y ≥ 0 \).
Значение модуля \( |y| \) равно \( y \), если \( y ≥ 0 \), и равно \( -y \), если \( y < 0 \).
Для выполнения условия \( |y| — y = 0 \), необходимо:
\( |y| = y \).
Следовательно, \( y ≥ 0 \).
График уравнения:
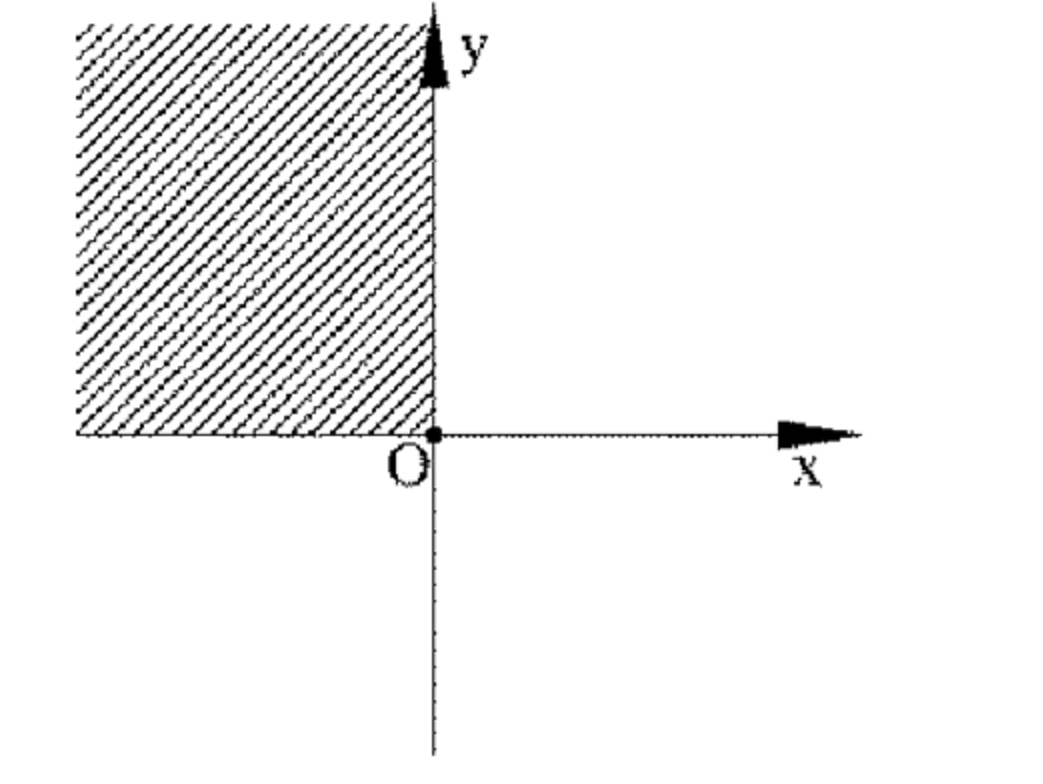
Уравнение \( |x| + |y| = y — x \) выполняется только во второй четверти координатной плоскости, где \( x ≤ 0 \) и \( y ≥ 0 \).
График представляет собой прямую линию, проходящую через точки:
— \( (0, 0) \);
— \( (-1, 1) \);
— \( (-2, 2) \).
Линия наклонена под углом \( 135^\circ \) к оси \( x \).
в) \( |x| + |y| = x — y \)
Преобразуем уравнение:
\( (|x| — x) + (|y| + y) = 0 \).
Рассмотрим каждое слагаемое отдельно.
Первое слагаемое:
\( |x| — x ≥ 0 \).
Значение модуля \( |x| \) равно \( x \), если \( x ≥ 0 \), и равно \( -x \), если \( x < 0 \).
Для выполнения условия \( |x| — x = 0 \), необходимо:
\( |x| = x \).
Следовательно, \( x ≥ 0 \).
Второе слагаемое:
\( |y| + y ≥ 0 \).
Значение модуля \( |y| \) равно \( y \), если \( y ≥ 0 \), и равно \( -y \), если \( y < 0 \).
Для выполнения условия \( |y| + y = 0 \), необходимо:
\( |y| = -y \).
Следовательно, \( y ≤ 0 \).
График уравнения:
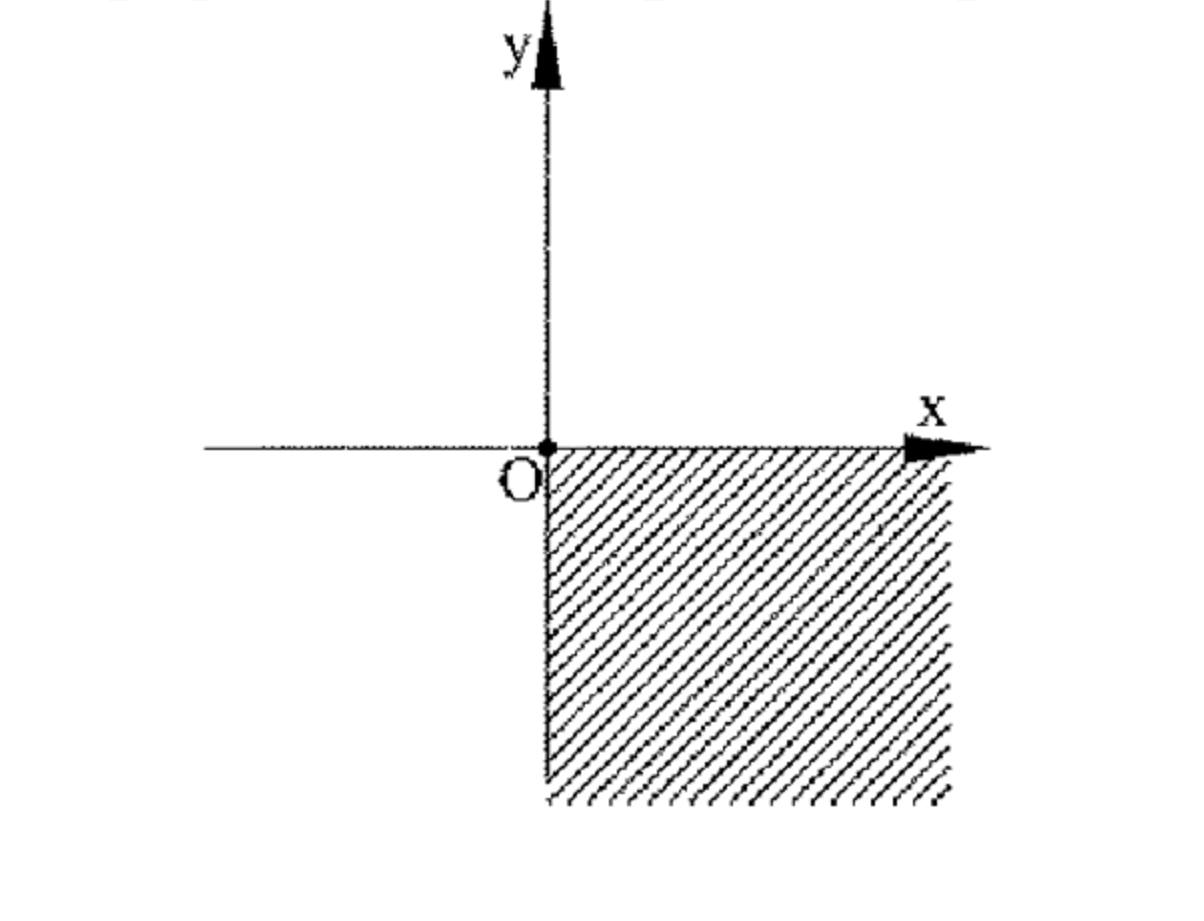
Уравнение \( |x| + |y| = x — y \) выполняется только в четвертой четверти координатной плоскости, где \( x ≥ 0 \) и \( y ≤ 0 \).
График представляет собой прямую линию, проходящую через точки:
— \( (0, 0) \);
— \( (1, -1) \);
— \( (2, -2) \).
Линия наклонена под углом \( -45^\circ \) к оси \( x \).
г) \( |x| + |y| = -x — y \)
Преобразуем уравнение:
\( (|x| + x) + (|y| + y) = 0 \).
Рассмотрим каждое слагаемое отдельно.
Первое слагаемое:
\( |x| + x ≥ 0 \).
Значение модуля \( |x| \) равно \( x \), если \( x ≥ 0 \), и равно \( -x \), если \( x < 0 \).
Для выполнения условия \( |x| + x = 0 \), необходимо:
\( |x| = -x \).
Следовательно, \( x ≤ 0 \).
Второе слагаемое:
\( |y| + y ≥ 0 \).
Значение модуля \( |y| \) равно \( y \), если \( y ≥ 0 \), и равно \( -y \), если \( y < 0 \).
Для выполнения условия \( |y| + y = 0 \), необходимо:
\( |y| = -y \).
Следовательно, \( y ≤ 0 \).
График уравнения:
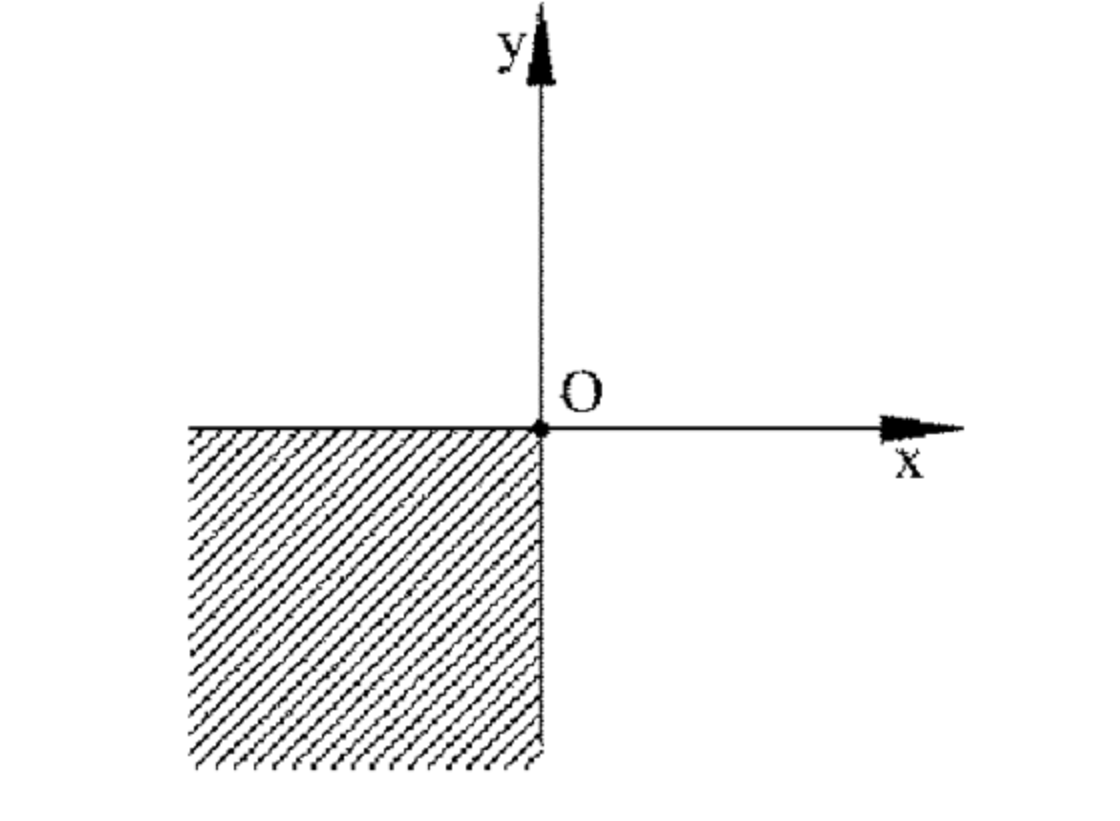
Уравнение \( |x| + |y| = -x — y \) выполняется только в третьей четверти координатной плоскости, где \( x ≤ 0 \) и \( y ≤ 0 \).
График представляет собой прямую линию, проходящую через точки:
— \( (0, 0) \);
— \( (-1, -1) \);
— \( (-2, -2) \).
Линия наклонена под углом \( -135^\circ \) к оси \( x \).