Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( (x — 1)^2 + (y — 2)^2 = 16 \);
б) \( (x — 1)^2 + (|y| — 2)^2 = 16 \);
в) \( (|x| — 1)^2 + (y — 2)^2 = 16 \);
г) \( (|x| — 1)^2 + (|y| — 2)^2 = 16 \)
Построить график уравнения:
а) \( (x — 1)^2 + (y — 2)^2 = 16 \);
Дано уравнение окружности:
\( x_0 = 1 \), \( y_0 = 2 \), \( R = 4 \);
График уравнения:
б) \( (x — 1)^2 + (|y| — 2)^2 = 16 \);
Если \( y \geq 0 \), тогда:
\( (x — 1)^2 + (y — 2)^2 = 16 \);
Дано уравнение окружности:
\( x_0 = 1 \), \( y_0 = 2 \), \( R = 16 \);
График симметричен относительно оси абсцисс:
в) \( (|x| — 1)^2 + (y — 2)^2 = 16 \);
Если \( x \geq 0 \), тогда:
\( (x — 1)^2 + (y — 2)^2 = 16 \);
Дано уравнение окружности:
\( x_0 = 1 \), \( y_0 = 2 \), \( R = 16 \);
График симметричен относительно оси ординат:
г) \( (|x| — 1)^2 + (|y| — 2)^2 = 16 \);
Если \( x \geq 0 \) и \( y \geq 0 \), тогда:
\( (x — 1)^2 + (y — 2)^2 = 16 \);
Дано уравнение окружности:
\( x_0 = 1 \), \( y_0 = 2 \), \( R = 16 \);
График симметричен относительно осей координат:
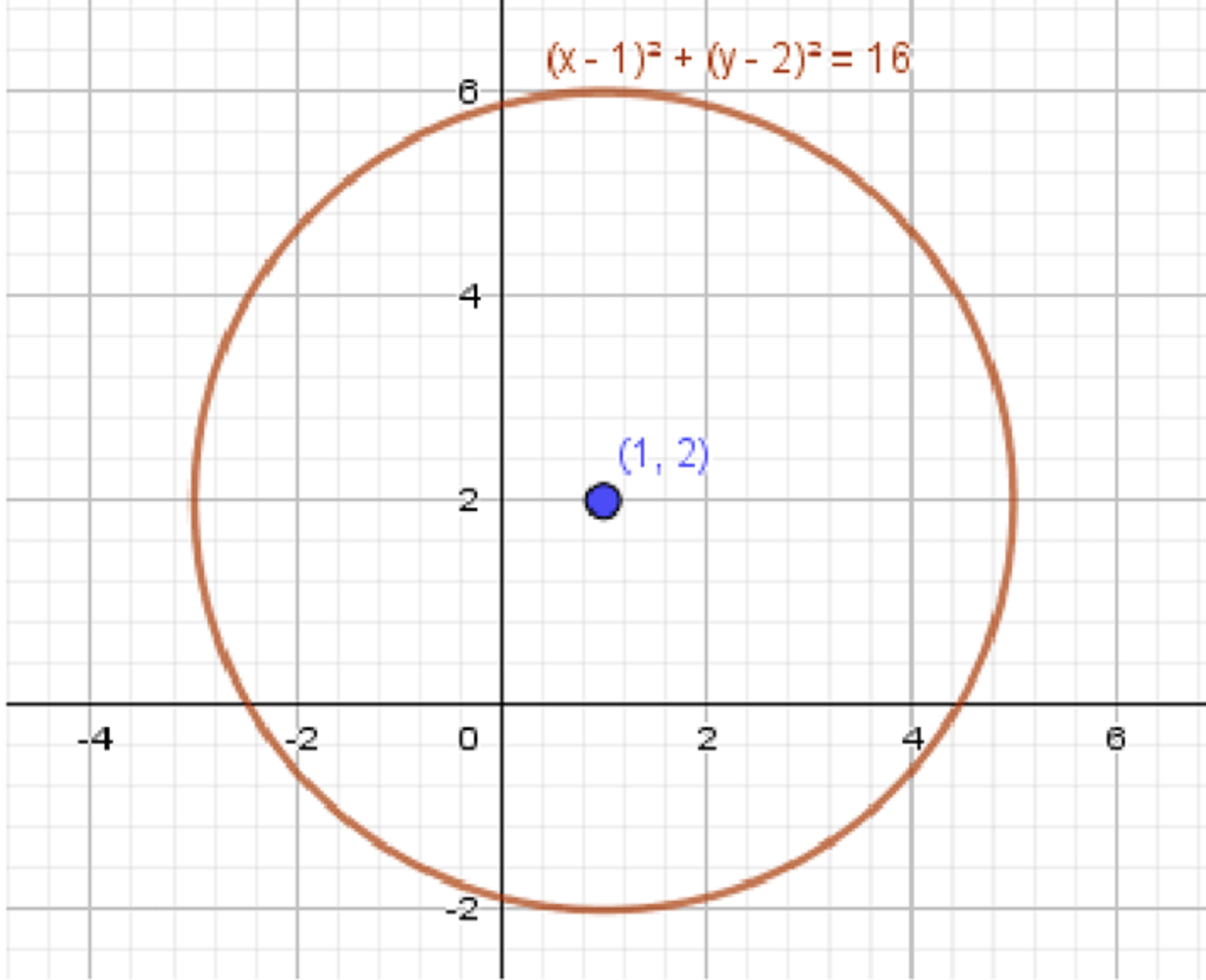
а) \( (x — 1)^2 + (y — 2)^2 = 16 \)
Дано уравнение окружности:
- Центр окружности: \( x_0 = 1 \), \( y_0 = 2 \)
- Радиус окружности: \( R = 4 \), так как \( R = \sqrt{16} \)
Уравнение окружности имеет вид:
\( (x — x_0)^2 + (y — y_0)^2 = R^2 \)
Подставляем значения \( x_0 = 1 \), \( y_0 = 2 \), \( R = 4 \):
\( (x — 1)^2 + (y — 2)^2 = 16 \)
График представляет собой окружность с центром в точке \( (1; 2) \) и радиусом \( R = 4 \).
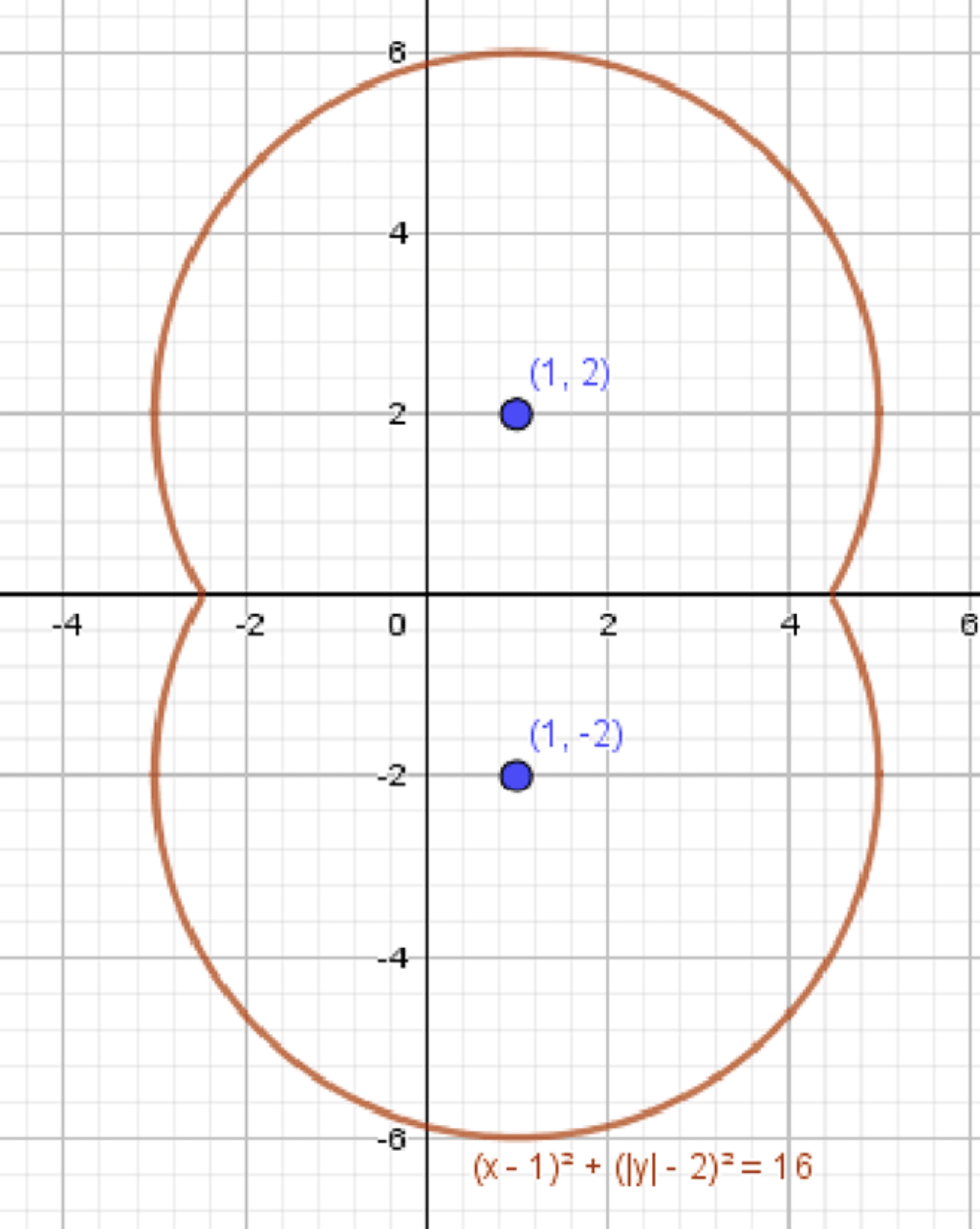
б) \( (x — 1)^2 + (|y| — 2)^2 = 16 \)
Если \( y \geq 0 \), то уравнение принимает вид:
\( (x — 1)^2 + (y — 2)^2 = 16 \)
Дано уравнение окружности:
- Центр окружности: \( x_0 = 1 \), \( y_0 = 2 \)
- Радиус окружности: \( R = 4 \), так как \( R = \sqrt{16} \)
Для отрицательных значений \( y \) график симметричен относительно оси абсцисс.
Таким образом, график состоит из двух частей: верхняя часть окружности для \( y \geq 0 \) и симметричная нижняя часть для \( y < 0 \).
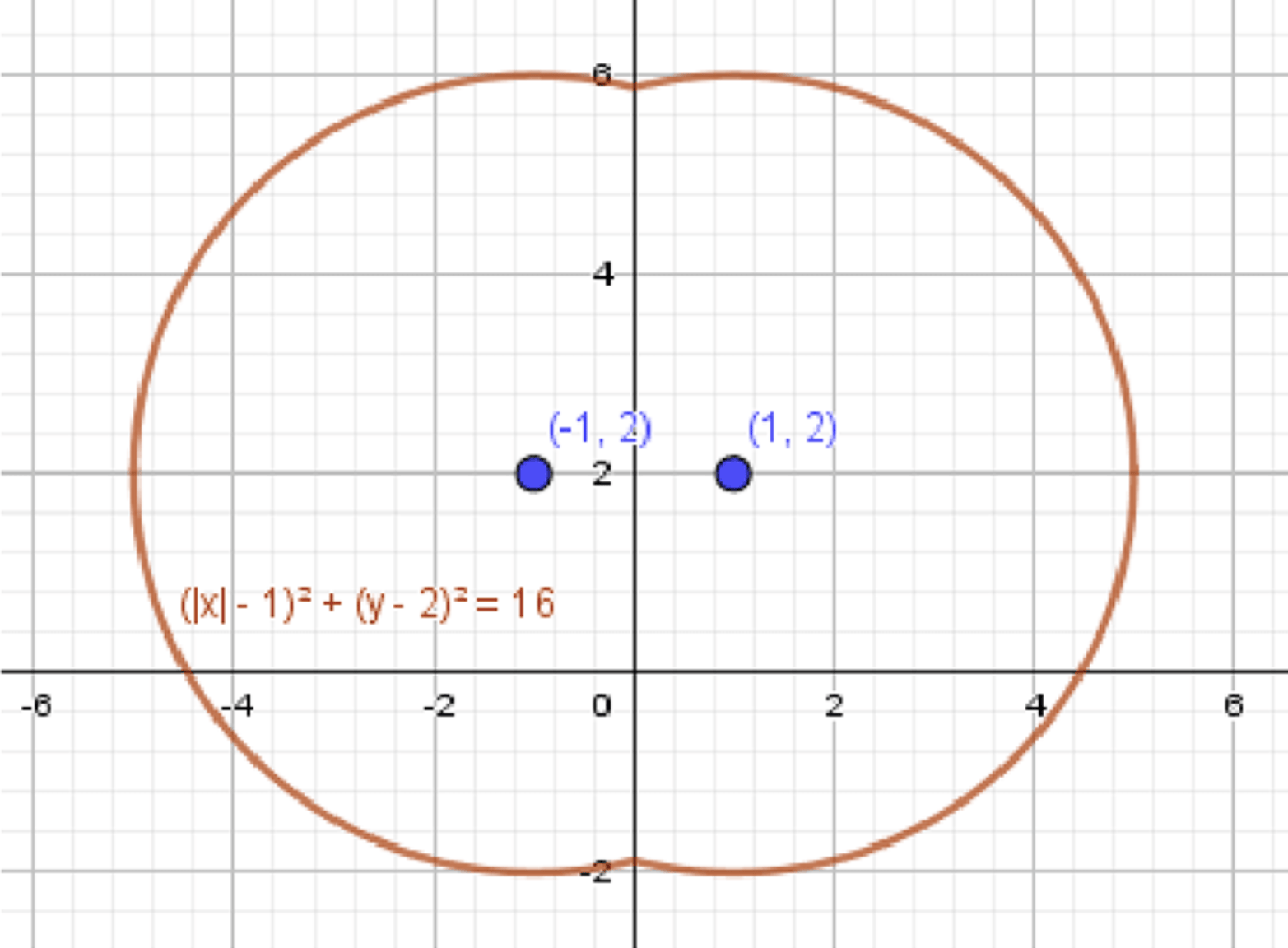
в) \( (|x| — 1)^2 + (y — 2)^2 = 16 \)
Если \( x \geq 0 \), то уравнение принимает вид:
\( (x — 1)^2 + (y — 2)^2 = 16 \)
Дано уравнение окружности:
- Центр окружности: \( x_0 = 1 \), \( y_0 = 2 \)
- Радиус окружности: \( R = 4 \), так как \( R = \sqrt{16} \)
Для отрицательных значений \( x \) график симметричен относительно оси ординат.
Таким образом, график состоит из двух частей: правая часть окружности для \( x \geq 0 \) и симметричная левая часть для \( x < 0 \).
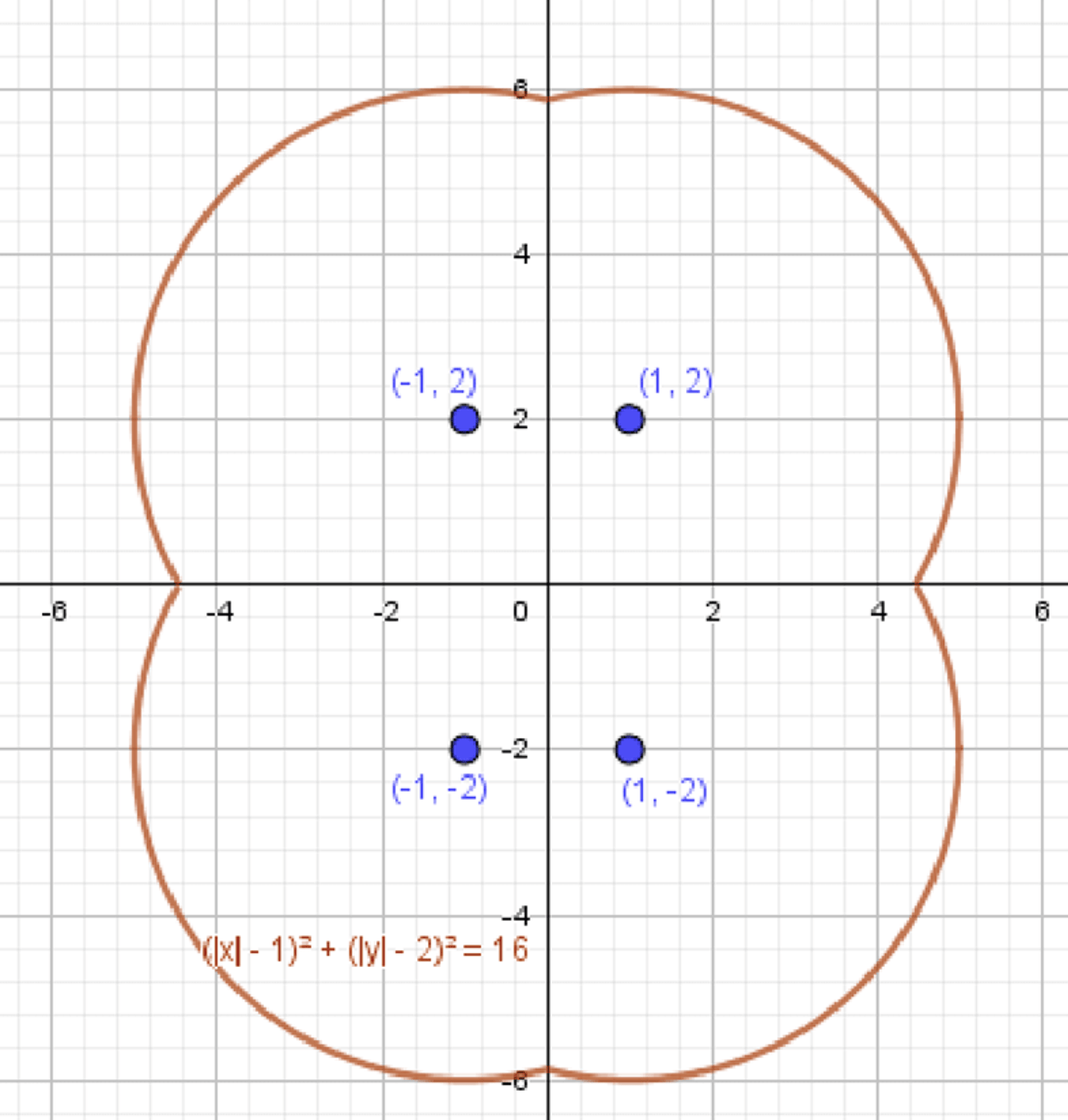
г) \( (|x| — 1)^2 + (|y| — 2)^2 = 16 \)
Если \( x \geq 0 \) и \( y \geq 0 \), то уравнение принимает вид:
\( (x — 1)^2 + (y — 2)^2 = 16 \)
Дано уравнение окружности:
- Центр окружности: \( x_0 = 1 \), \( y_0 = 2 \)
- Радиус окружности: \( R = 4 \), так как \( R = \sqrt{16} \)
Для отрицательных значений \( x \) и \( y \) график симметричен относительно осей координат.
Таким образом, график состоит из четырех частей: верхняя правая часть окружности для \( x \geq 0 \), \( y \geq 0 \), верхняя левая часть для \( x < 0 \), \( y \geq 0 \), нижняя правая часть для \( x \geq 0 \), \( y < 0 \), и нижняя левая часть для \( x < 0 \), \( y < 0 \).