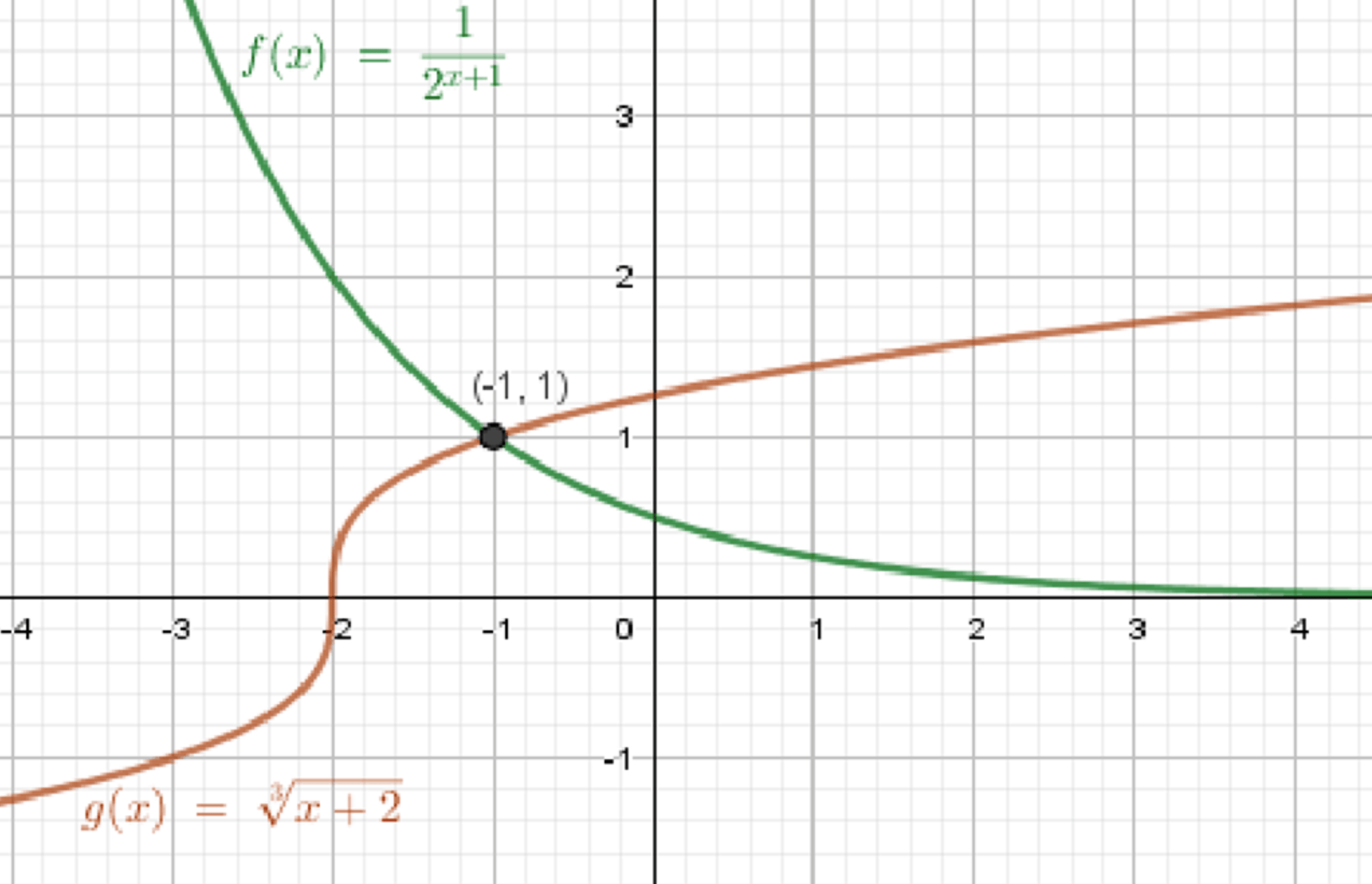Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 59.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( \left\{\begin{array}{l} y \cdot 2^{x+1}=1 \\ \sqrt[3]{x+2}=y \end{array} \right.\)
б) \( \left\{\begin{array}{l} y=2^{x-1} \\ |x-3|=y+1 \end{array} \right.\)
Решить графически систему уравнений:
а) \( \left\{\begin{array}{l} y \cdot 2^{x+1}=1 \\ \sqrt[3]{x+2}=y \end{array}\right. \Rightarrow \left\{\begin{array}{l} y=2^{-x-1} \\ y=\sqrt[3]{x+2} ; \end{array}\right. \)
\( y=2^{-x-1} \) — показательная функция:
\( \begin{array}{|c|c|c|c|} \hline x & -3 & -2 & -1 \\ \hline y & 4 & 2 & 1 \\ \hline \end{array} \)
\( y=\sqrt[3]{x+2} \) — кубическая парабола:
\( x_{0}=-2, y_{0}=0; \)
\( \begin{array}{|c|c|c|} \hline x & -1 & 6 \\ \hline y & 1 & 2 \\ \hline \end{array} \)
Графики функций:
Ответ: \( (-1 ; 1) \).
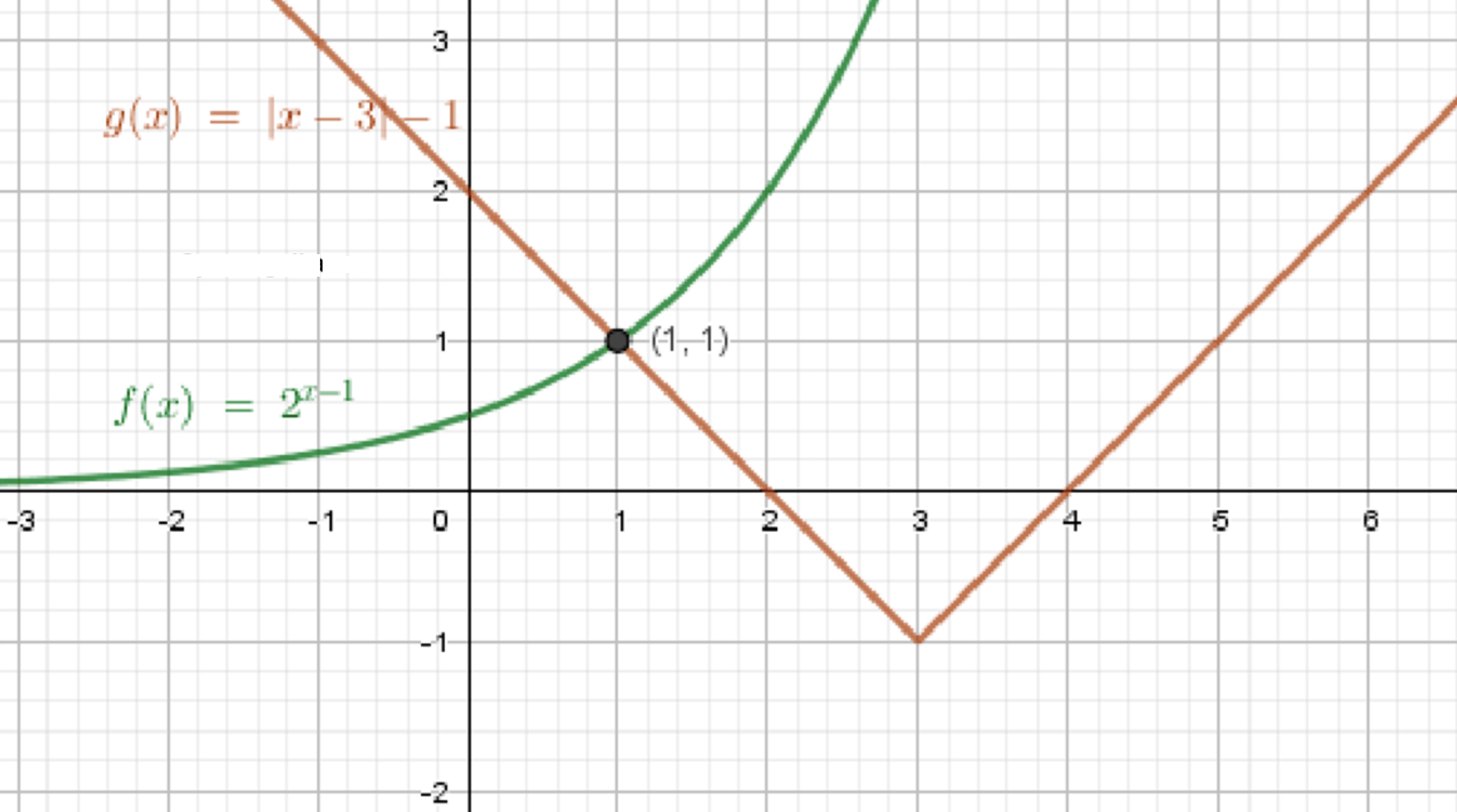
б) \( \left\{\begin{array}{l} y=2^{x-1} \\ |x-3|=y+1 \end{array}\right. \Rightarrow \left\{\begin{array}{l} y=2^{x-1} \\ y=|x-3|-1 ; \end{array}\right. \)
\( y=2^{x-1} \) — показательная функция:
\( \begin{array}{|c|c|c|c|} \hline x & 1 & 2 & 3 \\ \hline y & 1 & 2 & 4 \\ \hline \end{array} \)
\( y=|x-3|-1 \) — уравнение ломаной:
\( x_{0}=3, y_{0}=-1; \)
\( \begin{array}{|c|c|c|} \hline x & 2 & 4 \\ \hline y & 0 & 0 \\ \hline \end{array} \)
Графики функций:
Ответ: \( (1 ; 1) \).
а) Решить графически систему уравнений:
Система уравнений задана:
\( \left\{\begin{array}{l} y \cdot 2^{x+1}=1 \\ \sqrt[3]{x+2}=y \end{array}\right. \).
Преобразуем каждое уравнение системы:
- Из первого уравнения:\( y \cdot 2^{x+1}=1 \).Разделим обе части на \( 2^{x+1} \):\( y=\frac{1}{2^{x+1}}=2^{-x-1} \).
Таким образом, первое уравнение принимает вид:
\( y=2^{-x-1} \).
- Второе уравнение остается без изменений:\( y=\sqrt[3]{x+2} \).
Итак, система преобразована в вид:
\( \left\{\begin{array}{l} y=2^{-x-1} \\ y=\sqrt[3]{x+2} ; \end{array}\right. \).
Рассмотрим каждую функцию отдельно:
- Функция \( y=2^{-x-1} \) — показательная.Построим таблицу значений:\( \begin{array}{|c|c|c|c|} \hline x & -3 & -2 & -1 \\ \hline y & 4 & 2 & 1 \\ \hline \end{array} \).График этой функции убывает.
- Функция \( y=\sqrt[3]{x+2} \) — кубическая парабола.Определим координаты вершины:\( x_{0}=-2, y_{0}=0 \).Построим таблицу значений:
\( \begin{array}{|c|c|c|} \hline x & -1 & 6 \\ \hline y & 1 & 2 \\ \hline \end{array} \).
График этой функции возрастает.
Пересечение графиков функций:
Графики функций пересекаются в точке \( (-1 ; 1) \).
Ответ: \( (-1 ; 1) \).
б) Решить графически систему уравнений:
Система уравнений задана:
\( \left\{\begin{array}{l} y=2^{x-1} \\ |x-3|=y+1 \end{array}\right. \).
Преобразуем каждое уравнение системы:
- Первое уравнение остается без изменений:\( y=2^{x-1} \).
- Второе уравнение:\( |x-3|=y+1 \).Выразим \( y \):\( y=|x-3|-1 \).
Итак, система преобразована в вид:
\( \left\{\begin{array}{l} y=2^{x-1} \\ y=|x-3|-1 ; \end{array}\right. \).
Рассмотрим каждую функцию отдельно:
- Функция \( y=2^{x-1} \) — показательная.Построим таблицу значений:\( \begin{array}{|c|c|c|c|} \hline x & 1 & 2 & 3 \\ \hline y & 1 & 2 & 4 \\ \hline \end{array} \).График этой функции возрастает.
- Функция \( y=|x-3|-1 \) — уравнение ломаной.Определим координаты вершины:\( x_{0}=3, y_{0}=-1 \).Построим таблицу значений:
\( \begin{array}{|c|c|c|} \hline x & 2 & 4 \\ \hline y & 0 & 0 \\ \hline \end{array} \).
График этой функции состоит из двух прямых, сходящихся в вершине.
Пересечение графиков функций:
Графики функций пересекаются в точке \( (1 ; 1) \).
Ответ: \( (1 ; 1) \).