Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 59.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Применяя графический метод, определите, сколько решений имеет система уравнений:
а) \(\begin{cases}
y = x^2 \\
y = {cos} x
\end{cases}\)
б) \(\begin{cases}
x^2 + y^2 = 4 \\
y = 2 — x^2
\end{cases}\)
в) \(\begin{cases}
y = {sin} x \\
y = 0,1x
\end{cases}\)
г) \(\begin{cases}
y + 2 = \sqrt{x + 4} \\
y + x^3 = 0
\end{cases}\)
Применяя графический метод, определить, сколько решений имеет система уравнений:
а) \(\begin{cases}
y = x^2 \\
y = {cos} x
\end{cases}\)
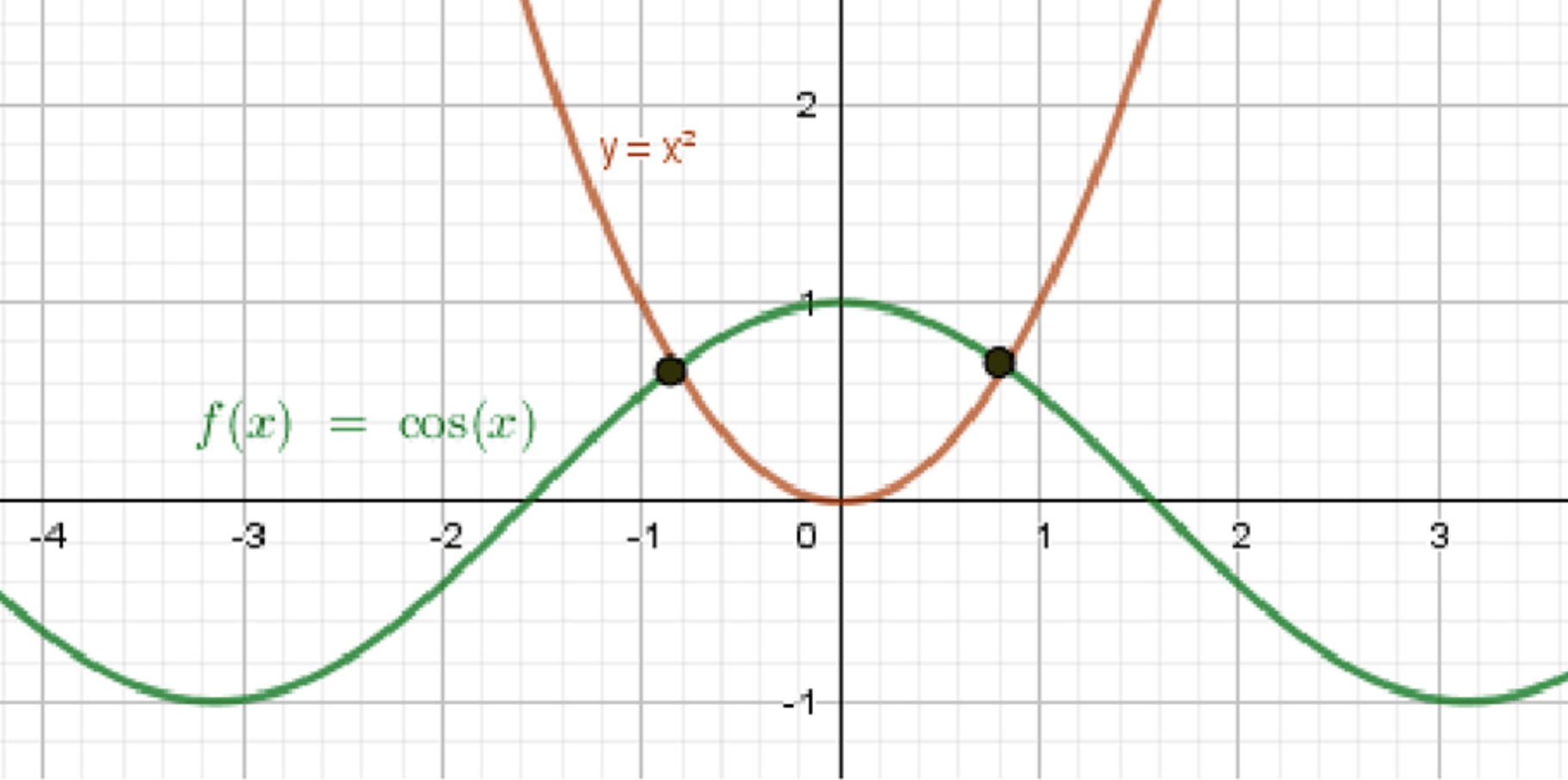
\(y = x^2\) — уравнение параболы:
\(x_0 = 0\), \(y_0 = 0\);
x | 1 | 2 | 3 |
|---|---|---|---|
y | 1 | 4 | 9 |
\(y = {cos} x\) — косинусоида;
Графики функций:
Ответ: 2 решения.
б) \(\begin{cases}
x^2 + y^2 = 4 \\
y = 2 — x^2
\end{cases}\)
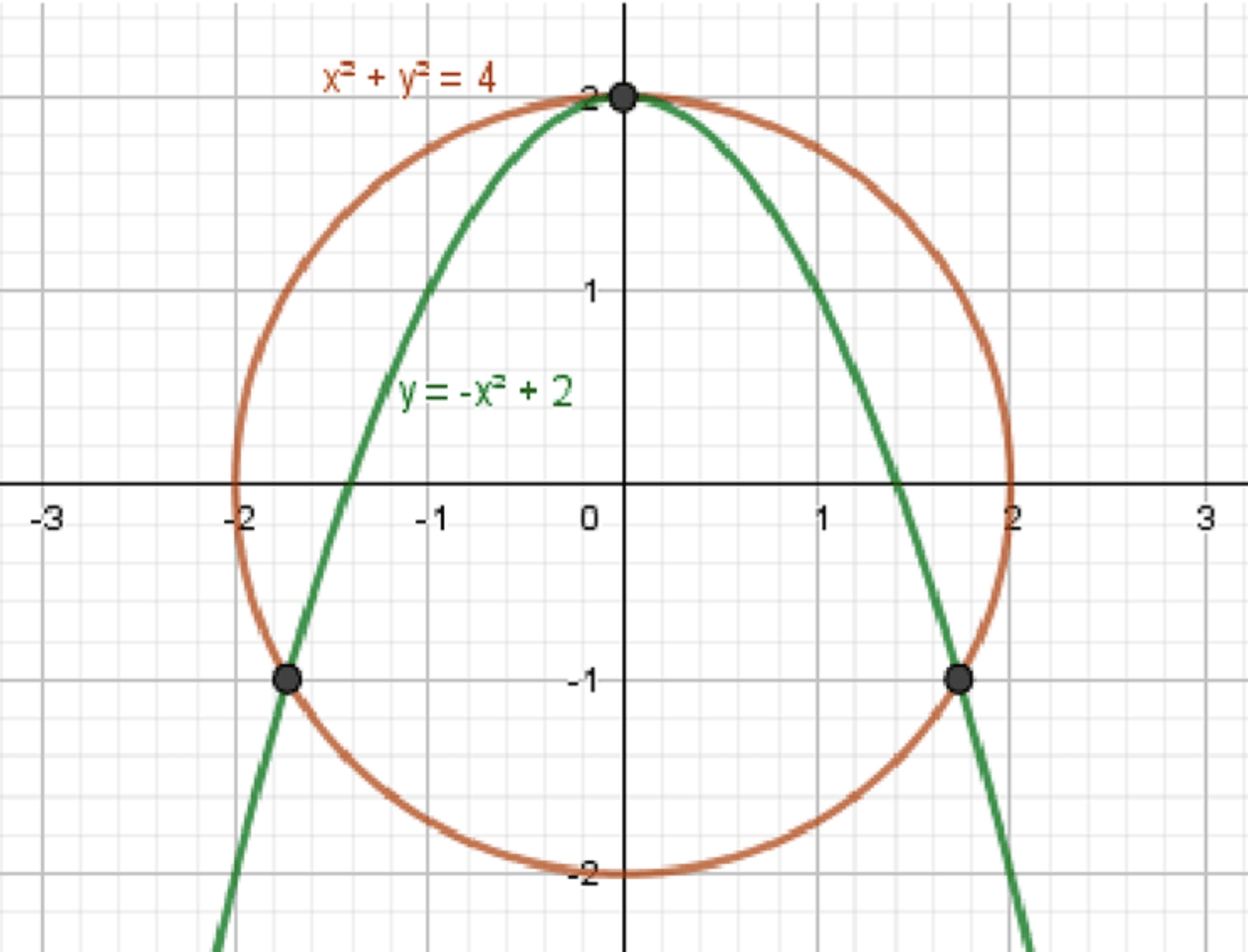
\(x^2 + y^2 = 4\) — уравнение окружности:
\(x_0 = 0\), \(y_0 = 0\), \(R = 2\);
\(y = 2 — x^2\) — уравнение параболы:
\(x_0 = 0\), \(y_0 = 2\);
x | 1 | 2 | 3 |
|---|---|---|---|
| y | 1 | -2 | -7 |
Графики функций:
Ответ: 3 решения.
в) \(\begin{cases}
y = {sin} x \\
y = 0,1x
\end{cases}\)
\(y = {sin} x\) — синусоида;
\(y = 0,1x\) — уравнение прямой:
x | 0 | 10 |
|---|---|---|
| y | 0 | 1 |
Графики функций:
Ответ: 7 решений.
г) \(\begin{cases}
y + 2 = \sqrt{x + 4} \\
y + x^3 = 0
\end{cases}
⇒
\begin{cases}
y = \sqrt{x + 4} — 2 \\
y = -x^3
\end{cases}\)
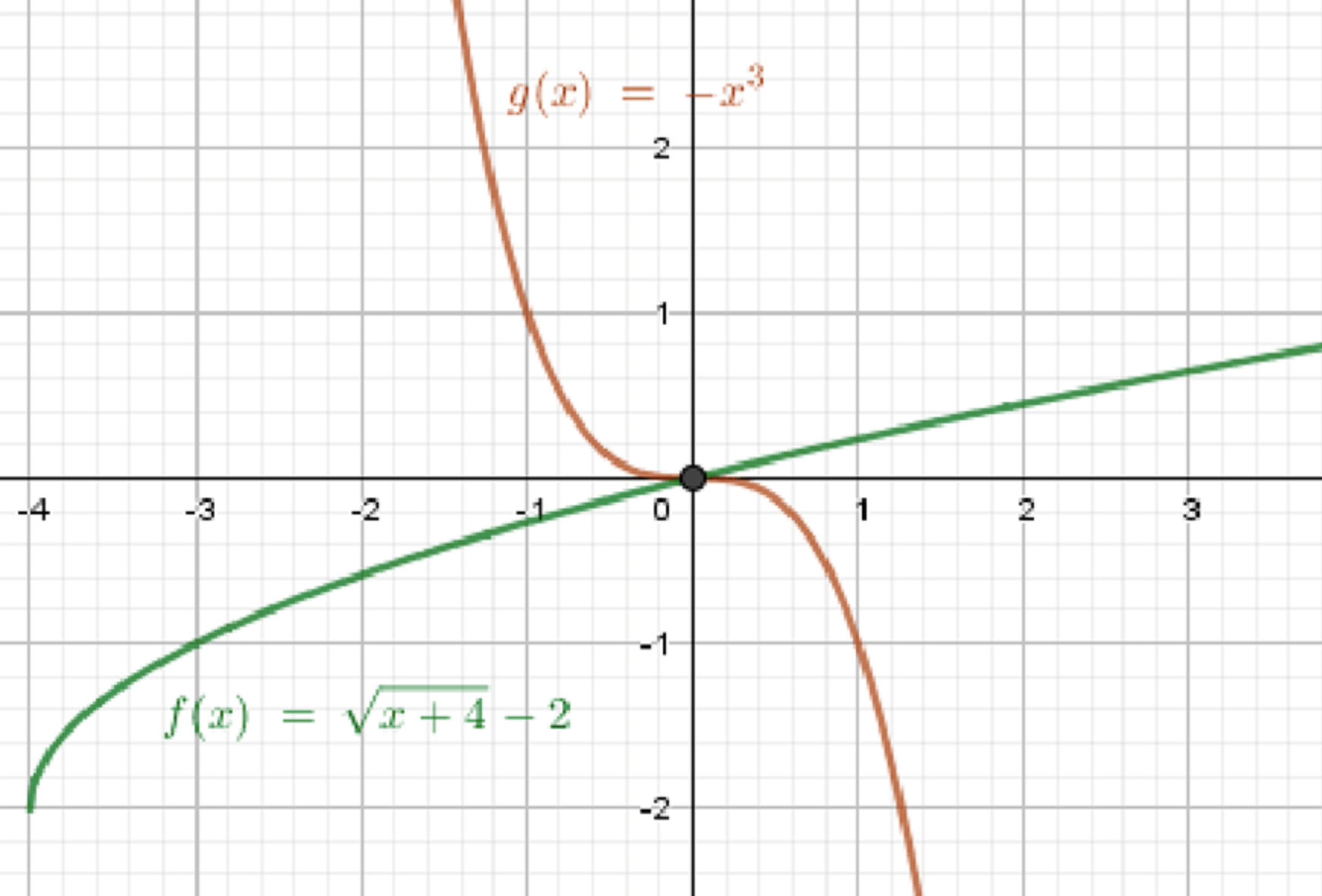
\(y = \sqrt{x + 4} — 2\) — ветвь параболы:
\(x_0 = -4\), \(y_0 = -2\);
x | -3 | 0 | 5 |
|---|---|---|---|
| y | -1 | 0 | 1 |
\(y = -x^3\) — уравнение параболы:
\(x_0 = 0\), \(y_0 = 0\);
x | 1 | 2 |
|---|---|---|
| y | -1 | -8 |
Графики функций:
Ответ: 1 решение.
а) Рассмотрим систему уравнений:
\(\begin{cases}
y = x^2 \\
y = \cos x
\end{cases}\)
Первое уравнение \(y = x^2\) описывает параболу, которая имеет вершину в точке \((x_0 = 0, y_0 = 0)\).
Для построения графика параболы найдем несколько точек, подставляя значения \(x\) в уравнение:
| x | 1 | 2 | 3 |
|---|---|---|---|
| y | 1 | 4 | 9 |
График параболы проходит через точки \((1, 1)\), \((2, 4)\) и \((3, 9)\).
Второе уравнение \(y = \cos x\) описывает косинусоиду. График функции \(y = \cos x\) является периодическим, с амплитудой 1 и периодом \(2\pi\).
Он проходит через точки \((0, 1)\), \((\pi, -1)\), \((2\pi, 1)\), и так далее.
Графики функций пересекаются в двух точках, что можно увидеть при их построении.
Ответ: 2 решения.
б) Рассмотрим систему уравнений:
\(\begin{cases}
x^2 + y^2 = 4 \\
y = 2 — x^2
\end{cases}\)
Первое уравнение \(x^2 + y^2 = 4\) описывает окружность с центром в точке \((x_0 = 0, y_0 = 0)\) и радиусом \(R = 2\).
График окружности проходит через точки \((2, 0)\), \((-2, 0)\), \((0, 2)\), \((0, -2)\).
Второе уравнение \(y = 2 — x^2\) описывает параболу, которая имеет вершину в точке \((x_0 = 0, y_0 = 2)\).
Для построения графика параболы найдем несколько точек, подставляя значения \(x\) в уравнение:
| x | 1 | 2 | 3 |
|---|---|---|---|
| y | 1 | -2 | -7 |
График параболы проходит через точки \((1, 1)\), \((2, -2)\) и \((3, -7)\).
Графики функций пересекаются в трех точках, что можно увидеть при их построении.
Ответ: 3 решения.
в) Рассмотрим систему уравнений:
\(\begin{cases}
y = \sin x \\
y = 0,1x
\end{cases}\)
Первое уравнение \(y = \sin x\) описывает синусоиду. График функции \(y = \sin x\) является периодическим, с амплитудой 1 и периодом \(2\pi\).
Он проходит через точки \((0, 0)\), \((\pi, 0)\), \((2\pi, 0)\), и так далее.
Второе уравнение \(y = 0,1x\) описывает прямую. Для построения графика прямой найдем несколько точек, подставляя значения \(x\) в уравнение:
| x | 0 | 10 |
|---|---|---|
| y | 0 | 1 |
График прямой проходит через точки \((0, 0)\) и \((10, 1)\).
Графики функций пересекаются в семи точках, что можно увидеть при их построении.
Ответ: 7 решений.
г) Рассмотрим систему уравнений:
\(\begin{cases}
y + 2 = \sqrt{x + 4} \\
y + x^3 = 0
\end{cases}
⇒
\begin{cases}
y = \sqrt{x + 4} — 2 \\
y = -x^3
\end{cases}\)
Первое уравнение \(y = \sqrt{x + 4} — 2\) описывает ветвь параболы, которая начинается в точке \((x_0 = -4, y_0 = -2)\).
Для построения графика найдем несколько точек, подставляя значения \(x\) в уравнение:
| x | -3 | 0 | 5 |
|---|---|---|---|
| y | -1 | 0 | 1 |
График ветви параболы проходит через точки \((-3, -1)\), \((0, 0)\) и \((5, 1)\).
Второе уравнение \(y = -x^3\) описывает кубическую параболу, которая имеет вершину в точке \((x_0 = 0, y_0 = 0)\).
Для построения графика найдем несколько точек, подставляя значения \(x\) в уравнение:
| x | 1 | 2 |
|---|---|---|
| y | -1 | -8 |
График кубической параболы проходит через точки \((1, -1)\) и \((2, -8)\).
Графики функций пересекаются в одной точке, что можно увидеть при их построении.
Ответ: 1 решение.