ГДЗ 10-11 Класс Номер 59.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Решите графически систему уравнений:

а) \[
\begin{cases}
y + x = 3 \\
xy = 2
\end{cases}
\]

б) \[
\begin{cases}
y = x(x — 4) \\
y + 8 = 2x
\end{cases}
\]

Решить графически систему уравнений:

а) \[
\begin{cases}
y + x = 3 \\
xy = 2
\end{cases}
\Rightarrow
\begin{cases}
y = 3 — x \\
y = \frac{2}{x}
\end{cases};
\]

\( y = 3 — x \) — уравнение прямой:

\[
\begin{array}{c|c|c}
x & 0 & 3 \\
\hline
y & 3 & 0 \\
\end{array}
\]

\( y = \frac{2}{x} \) — уравнение гиперболы:

\( x_0 = 0, \; y_0 = 0; \)

\[
\begin{array}{c|c|c|c}
x & 0{,}5 & 1 & 2 \\
\hline
y & 4 & 2 & 1 \\
\end{array}
\]

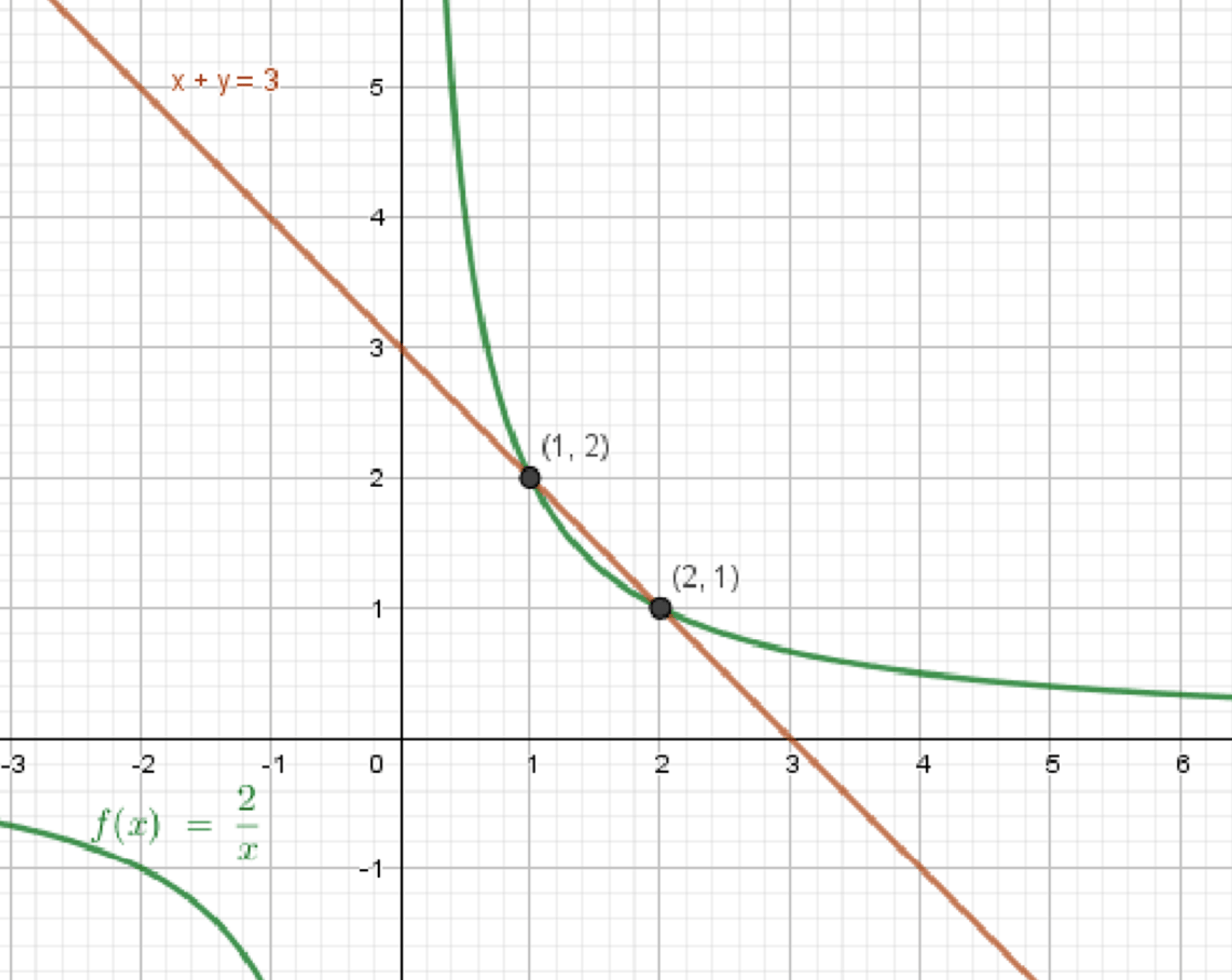
Графики функций:

Ответ: \( (1;\; 2);\; (2;\; 1) \).

б) \[
\begin{cases}
y = x(x — 4) \\
y + 8 = 2x
\end{cases}
\Rightarrow
\begin{cases}
y = x^2 — 4x \\
y = 2x — 8
\end{cases};
\]

\( y = x^2 — 4x \) — уравнение параболы:

\[
x_0 = -\frac{b}{2a} = -\frac{-4}{2 \cdot 1} = \frac{4}{2} = 2;
\]

\[
y_0 = 2^2 — 4 \cdot 2 = 4 — 8 = -4;
\]

\[
\begin{array}{c|c|c|c}
x & 3 & 4 & 5 \\
\hline
y & -3 & 0 & 5 \\
\end{array}
\]

\( y = 2x — 8 \) — уравнение прямой:

\[
\begin{array}{c|c|c}
x & 3 & 5 \\
\hline
y & -2 & 2 \\
\end{array}
\]

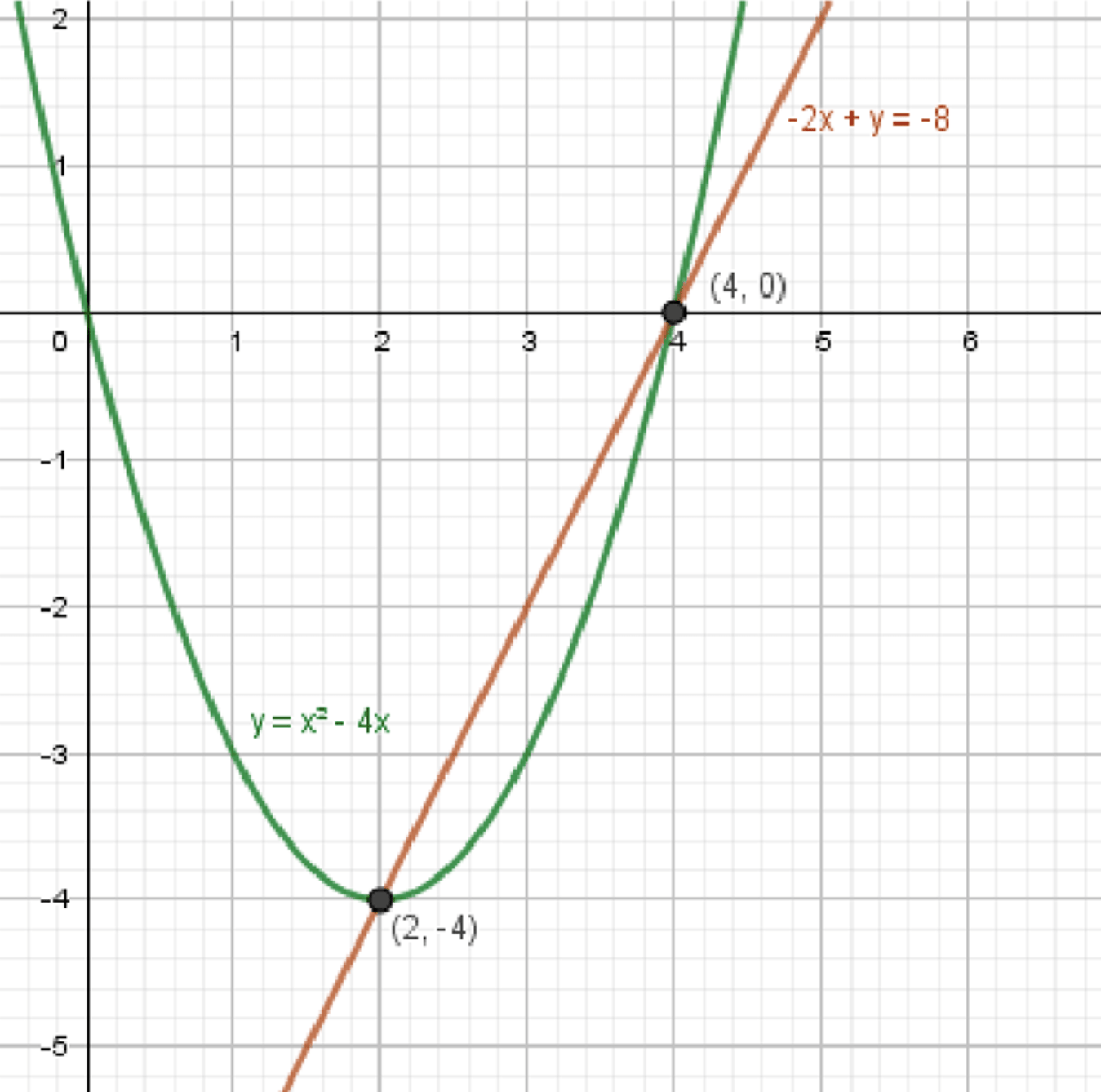
Графики функций:

Ответ: \( (2;\; -4);\; (4;\; 0) \).

Решить графически систему уравнений:

а) Рассмотрим систему уравнений:

\[
\begin{cases}
y + x = 3 \\
xy = 2
\end{cases}
\Rightarrow
\begin{cases}
y = 3 — x \\
y = \frac{2}{x}
\end{cases};
\]

Первое уравнение \( y + x = 3 \) можно преобразовать, выразив \( y \) через \( x \):

\[
y = 3 — x.
\]

Второе уравнение \( xy = 2 \) можно преобразовать, выразив \( y \) через \( x \):

\[
y = \frac{2}{x}.
\]

Таким образом, система уравнений сводится к двум функциям:

\[
\begin{cases}
y = 3 — x \\
y = \frac{2}{x}
\end{cases}.
\]

Рассмотрим график функции \( y = 3 — x \):

Это уравнение прямой, которая пересекает ось \( y \) в точке \((0; 3)\) и ось \( x \) в точке \((3; 0)\). Для построения графика найдем несколько точек:

\[
\begin{array}{c|c|c}
x & 0 & 3 \\
\hline
y & 3 & 0 \\
\end{array}
\]

График функции \( y = \frac{2}{x} \):

Это уравнение гиперболы, которая проходит через точки, где произведение \( x \cdot y = 2 \). Найдем несколько точек:

\[
\begin{array}{c|c|c|c}
x & 0{,}5 & 1 & 2 \\
\hline
y & 4 & 2 & 1 \\
\end{array}
\]

График функции \( y = \frac{2}{x} \) также имеет асимптоты: ось \( x \) и ось \( y \).

При построении графиков видно, что они пересекаются в двух точках. Найдем эти точки:

\[
\begin{cases}
y = 3 — x \\
y = \frac{2}{x}
\end{cases}.
\]

Подставим \( y = 3 — x \) во второе уравнение:

\[
x(3 — x) = 2 \Rightarrow 3x — x^2 = 2 \Rightarrow x^2 — 3x + 2 = 0.
\]

Решим квадратное уравнение:

\(x = \frac{-b \pm \sqrt{b^2 — 4ac}}{2a} = \frac{-(-3) \pm \sqrt{(-3)^2 — 4 \cdot 1 \cdot 2}}{2 \cdot 1} = \frac{3 \pm \sqrt{9 — 8}}{2} = \frac{3 \pm 1}{2}.\)

Получаем два корня:

\[
x_1 = \frac{3 + 1}{2} = 2, \; x_2 = \frac{3 — 1}{2} = 1.
\]

Найдем соответствующие значения \( y \):

Для \( x_1 = 2 \): \( y = 3 — 2 = 1 \).
Для \( x_2 = 1 \): \( y = 3 — 1 = 2 \).

Таким образом, точки пересечения графиков: \( (2; 1) \) и \( (1; 2) \).

Ответ: \( (1;\; 2);\; (2;\; 1) \).

б) Рассмотрим систему уравнений:

\[
\begin{cases}
y = x(x — 4) \\
y + 8 = 2x
\end{cases}
\Rightarrow
\begin{cases}
y = x^2 — 4x \\
y = 2x — 8
\end{cases}.
\]

Первое уравнение \( y = x(x — 4) \) можно преобразовать:

\[
y = x^2 — 4x.
\]

Второе уравнение \( y + 8 = 2x \) можно преобразовать:

\[
y = 2x — 8.
\]

Таким образом, система уравнений сводится к двум функциям:

\[
\begin{cases}
y = x^2 — 4x \\
y = 2x — 8
\end{cases}.
\]

Рассмотрим график функции \( y = x^2 — 4x \):

Это уравнение параболы. Найдем вершину параболы:

\[
x_0 = -\frac{b}{2a} = -\frac{-4}{2 \cdot 1} = \frac{4}{2} = 2.
\]

Найдем значение \( y_0 \) в вершине:

\[
y_0 = 2^2 — 4 \cdot 2 = 4 — 8 = -4.
\]

Для построения графика найдем несколько точек:

\[
\begin{array}{c|c|c|c}
x & 3 & 4 & 5 \\
\hline
y & -3 & 0 & 5 \\
\end{array}
\]

График функции \( y = 2x — 8 \):

Это уравнение прямой. Найдем несколько точек:

\[
\begin{array}{c|c|c}
x & 3 & 5 \\
\hline
y & -2 & 2 \\
\end{array}
\]

При построении графиков видно, что они пересекаются в двух точках. Найдем эти точки:

\[
\begin{cases}
y = x^2 — 4x \\
y = 2x — 8
\end{cases}.
\]

Подставим \( y = 2x — 8 \) в первое уравнение:

\[
x^2 — 4x = 2x — 8 \Rightarrow x^2 — 6x + 8 = 0.
\]

Решим квадратное уравнение:

\(x = \frac{-b \pm \sqrt{b^2 — 4ac}}{2a} = \frac{-(-6) \pm \sqrt{(-6)^2 — 4 \cdot 1 \cdot 8}}{2 \cdot 1} = \frac{6 \pm \sqrt{36 — 32}}{2} = \frac{6 \pm 2}{2}.\)

Получаем два корня:

\[
x_1 = \frac{6 + 2}{2} = 4, \; x_2 = \frac{6 — 2}{2} = 2.
\]

Найдем соответствующие значения \( y \):

Для \( x_1 = 4 \): \( y = 2 \cdot 4 — 8 = 0 \).
Для \( x_2 = 2 \): \( y = 2 \cdot 2 — 8 = -4 \).

Таким образом, точки пересечения графиков: \( (4; 0) \) и \( (2; -4) \).

Ответ: \( (2;\; -4);\; (4;\; 0) \).