ГДЗ 10-11 Класс Номер 7.22 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y={\cos }^{2}x+{\sin }^{2}x$

б) $y={\cos }^2\frac{1}{x}+{\sin }^2\frac{1}{x}$

в) $y={\sin }^2\sqrt{x}+{\cos }^2\sqrt{x}$

г) $y={\sin }^2\frac{1}{x^2-4}+{\cos }^2\frac{1}{x^2-4}$

Построить график функции:

а) $y = \cos^2 x + \sin^2 x = 1$;

Область определения:
$x \in \mathbb{R}$;

График функции:

б) $y = \cos^2 \frac{1}{x} + \sin^2 \frac{1}{x} = 1$;

Область определения:
$x \neq 0$;

График функции:

в) $y = \sin^2 \sqrt{x} + \cos^2 \sqrt{x} = 1$;

Область определения:
$x \geq 0$;

График функции:

г) $y = \sin^2 \frac{1}{x^2 — 4} + \cos^2 \frac{1}{x^2 — 4} = 1$;

Область определения:
$x^2 — 4 \neq 0$;
$x^2 \neq 4$;
$x \neq \pm 2$;

График функции:

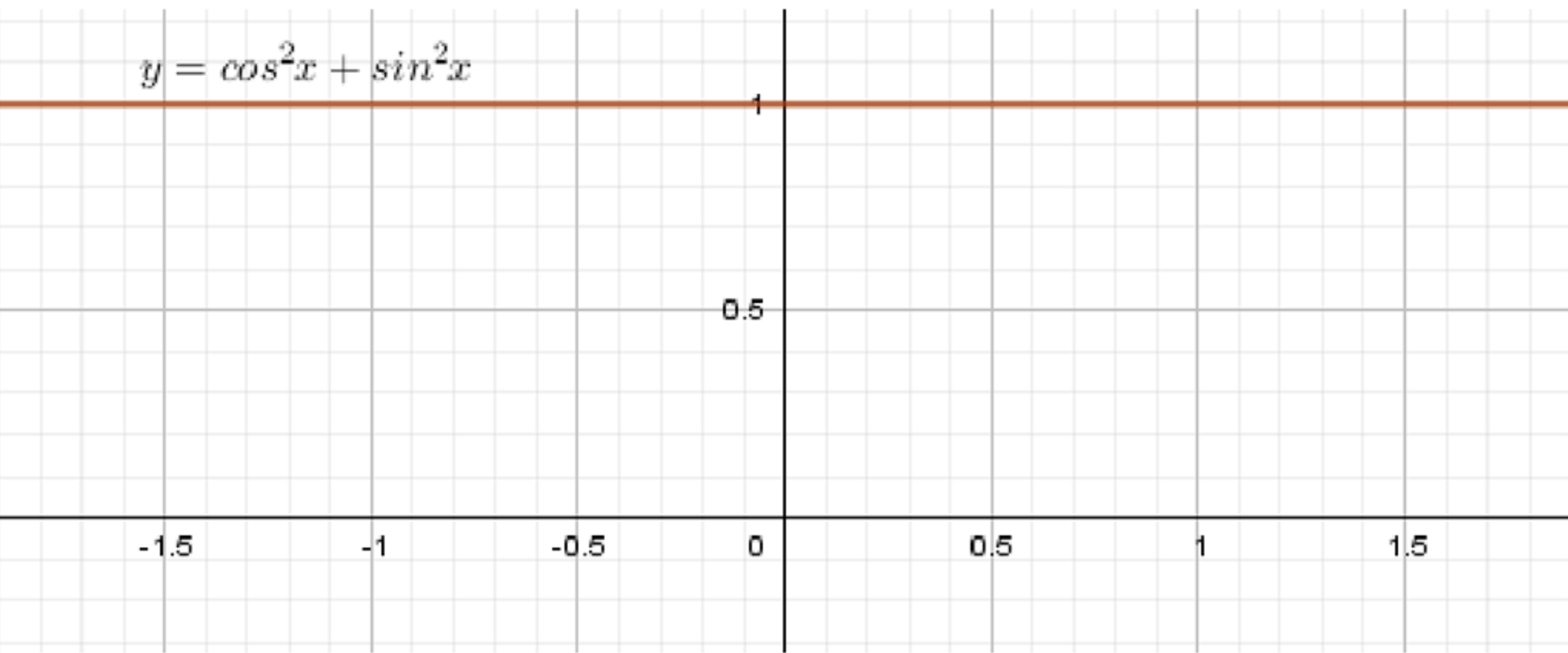
а) $y = \cos^2 x + \sin^2 x = 1$

1) Область определения:

Для функции $y = \cos^2 x + \sin^2 x$, важно помнить, что это стандартное тригонометрическое тождество, которое всегда истинно для всех значений $x$. То есть, для любого значения $x$ на оси действительных чисел выполняется:

$$\cos^2 x + \sin^2 x = 1$$

Таким образом, область определения:

$$x \in \mathbb{R}$$

2) График функции:

График функции $y = 1$ — это горизонтальная прямая, расположенная на уровне $y = 1$ на координатной плоскости. Так как выражение $\cos^2 x + \sin^2 x$ всегда равно 1, независимо от $x$, график будет представлять собой прямую линию, параллельную оси $x$, которая проходит через точку $y = 1$.

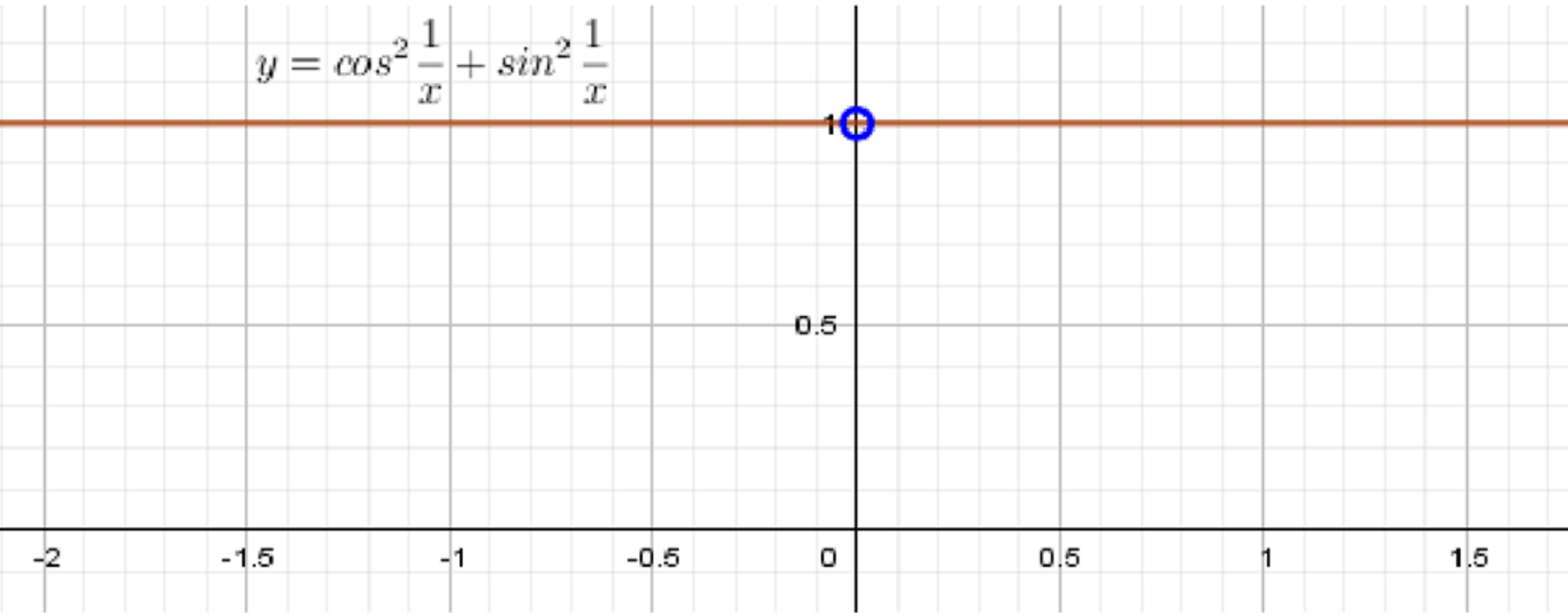
б) $y = \cos^2 \frac{1}{x} + \sin^2 \frac{1}{x} = 1$

1) Область определения:

Функция $y = \cos^2 \frac{1}{x} + \sin^2 \frac{1}{x}$ также является тригонометрическим тождеством, аналогичным предыдущему. Важно отметить, что выражение имеет вид:

$$\cos^2 \left( \frac{1}{x} \right) + \sin^2 \left( \frac{1}{x} \right) = 1$$

Однако есть ограничение на $x$, так как деление на ноль невозможно. Таким образом, область определения:

$$x \neq 0$$

2) График функции:

График этой функции будет аналогичен графику из пункта (а), то есть функцией будет являться постоянное значение $y = 1$, но с тем отличием, что график существует только для $x \neq 0$. Этот график будет представлять собой горизонтальную прямую на уровне $y = 1$, но с исключением точки $x = 0$, где функция не определена.

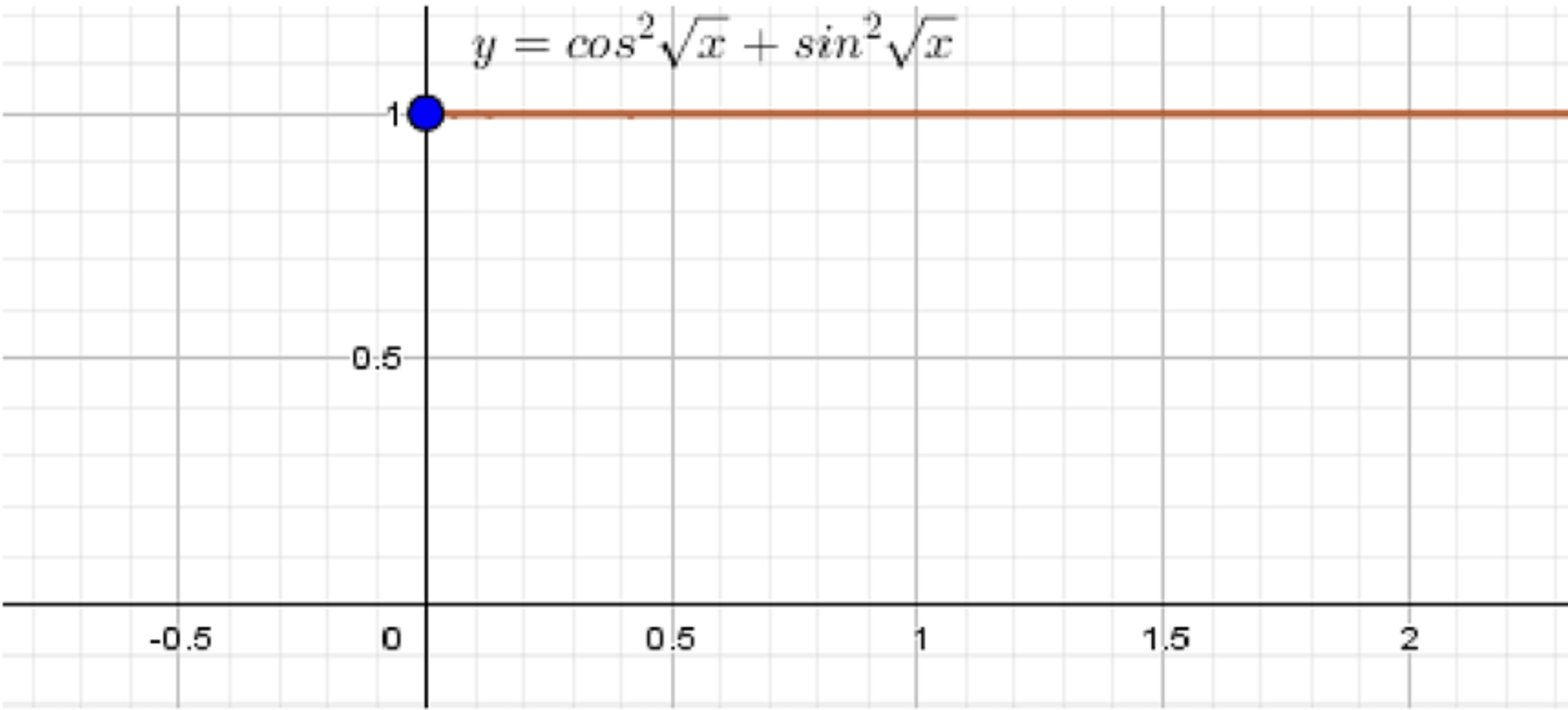
в) $y = \sin^2 \sqrt{x} + \cos^2 \sqrt{x} = 1$

1) Область определения:

В данном случае мы рассматриваем функцию с аргументом $\sqrt{x}$. Поскольку $\sqrt{x}$ определено только для неотрицательных $x$, то область определения будет:

$$x \geq 0$$

Таким образом, область определения функции: $x \in [0, +\infty)$.

2) График функции:

Это снова стандартное тригонометрическое тождество. Функция $y = \sin^2 \sqrt{x} + \cos^2 \sqrt{x} = 1$ для любого $x \geq 0$, так как:

$$\sin^2 \sqrt{x} + \cos^2 \sqrt{x} = 1$$

Следовательно, график будет представлять собой горизонтальную прямую $y = 1$ на промежутке $x \geq 0$. Для значений ( x < 0 \ функция не существует.

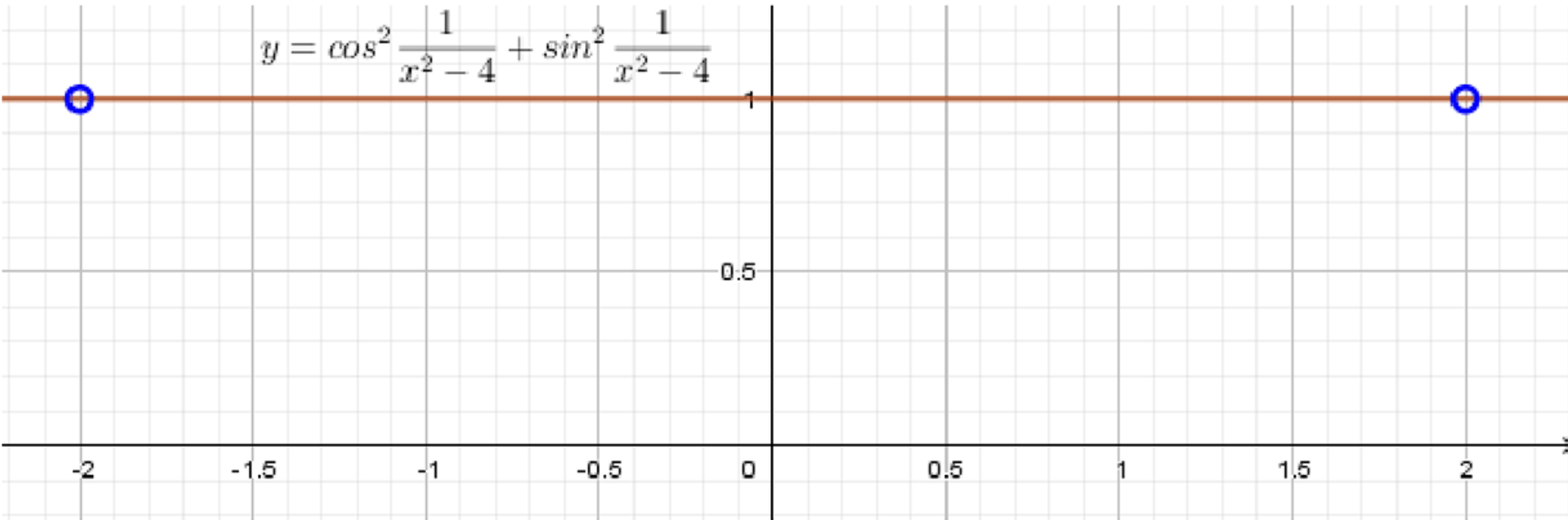
г) $y = \sin^2 \frac{1}{x^2 — 4} + \cos^2 \frac{1}{x^2 — 4} = 1$

1) Область определения:

Здесь важно обратить внимание на выражение $\frac{1}{x^2 — 4}$. Для того чтобы функция была определена, знаменатель не должен быть равен нулю, а значит:

$$x^2 — 4 \neq 0 \quad \Rightarrow \quad x^2 \neq 4 \quad \Rightarrow \quad x \neq \pm 2$$

Таким образом, область определения функции:

$$x \neq \pm 2$$

2) График функции:

Как и в предыдущих случаях, выражение $\sin^2 \frac{1}{x^2 — 4} + \cos^2 \frac{1}{x^2 — 4} = 1$ всегда истинно. Однако для $x = \pm 2$ функция не существует, так как деление на ноль невозможно.

График будет представлять собой горизонтальную прямую $y = 1$ с исключением точек $x = 2$ и $x = -2$, где функция не определена.