ГДЗ 10-11 Класс Номер 8.13 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

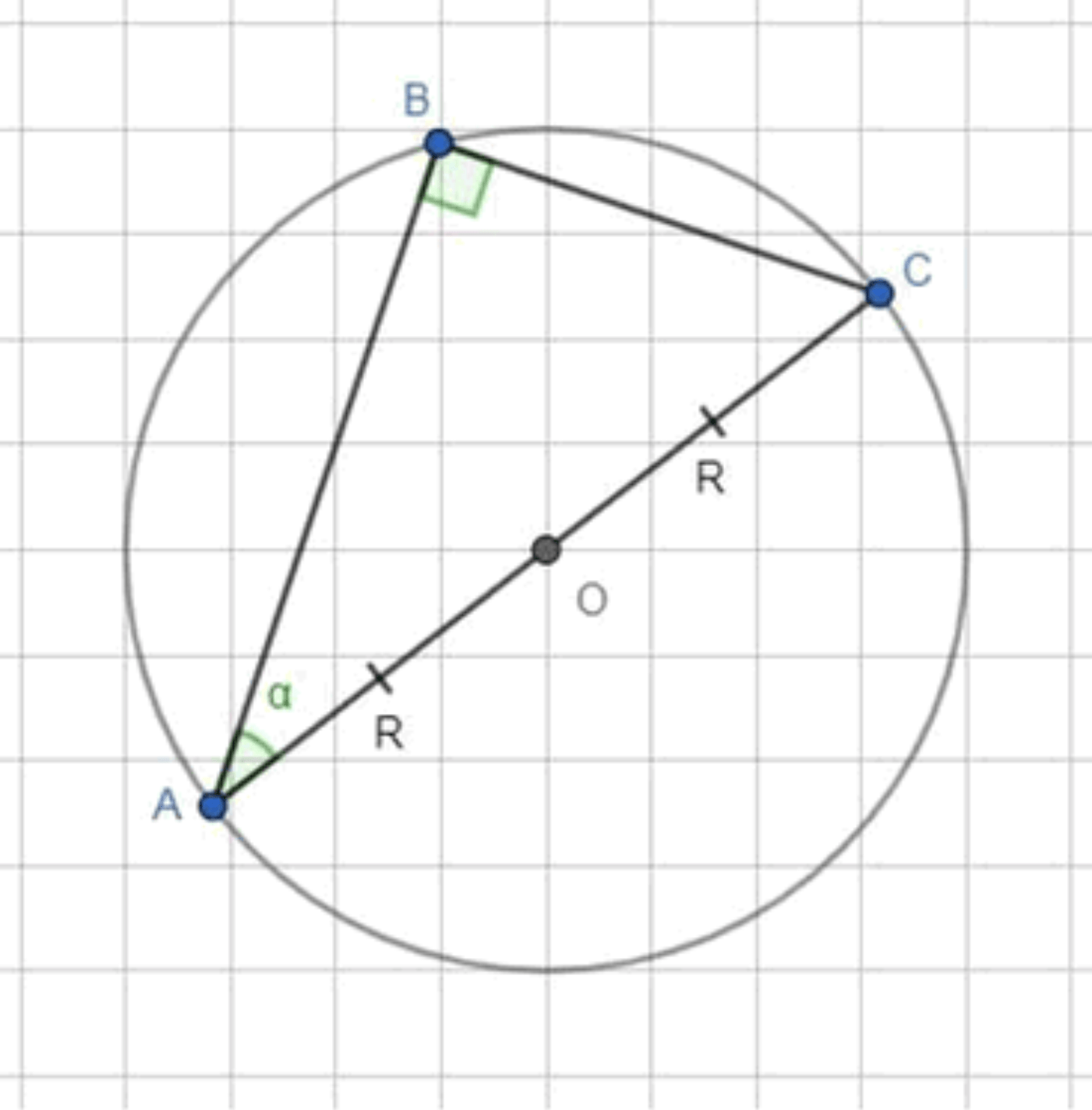
Хорда АВ образует с диаметром АС окружности угол а. Найдите длину хорды АВ, если радиус окружности равен R.

Хорда $AB$ образует с диаметром $AC$ окружности угол $a^\circ$;

Найти длину хорды $AB$, если радиус окружности равен $R$.

1) Отобразим условие задачи:

2) Так как $AC$ диаметр окружности:

$$AC = AO + OC = R + R = 2R;$$

3) Угол $B$ опирается на диаметр окружности, значит:

$$\angle ABC = 90^\circ;$$

4) Треугольник $ABC$ прямоугольный, следовательно:

$$\cos \angle A = \frac{AB}{AC};$$ $$AB = AC \cdot \cos \angle A = 2R \cdot \cos a;$$

Ответ: $2R \cos a$.

Есть окружность с центром $O$ и радиусом $R$. $AC$ — её диаметр, $AB$ — хорда. Хорда $AB$ образует с диаметром $AC$ угол $a^\circ$ в точке $A$ (то есть $\angle BAC = a$). Требуется найти длину хорды $AB$.

Важно: далее считаем, что $0^\circ<a<90^\circ$.
При $a=0^\circ$ хорда $AB$ «совпадает» с диаметром (деградация в отрезок диаметра),
при $a\ge 90^\circ$ треугольник с прямым углом в $B$ и углом $a$ в $A$ не существует (сумма углов > $180^\circ$).

Факт об угле, опирающемся на диаметр

Теорема Фалеса: всякий вписанный угол, опирающийся на диаметр, прямой.
Дуга, на которую опирается угол $\angle ABC$, — это дуга $AC$, а $AC$ — диаметр, значит

$$\angle ABC=90^\circ.$$

Длина диаметра через радиус

По определению диаметра:

$$AC = AO + OC = R + R = 2R.$$

Решение через прямоугольный треугольник (основной путь)

В треугольнике $ABC$ угол при $B$ прямой, значит $AC$ — гипотенуза, а стороны $AB$ и $BC$ — катеты.
Рассмотрим угол $\angle A=\angle BAC=a$. Для этого угла:

• прилежащий катет — $AB$;
• гипотенуза — $AC$.

По определению косинуса острого угла в прямоугольном треугольнике:

$$\cos a=\frac{\text{прилежащий катет}}{\text{гипотенуза}}=\frac{AB}{AC}.$$

Отсюда

$$AB=AC\cdot\cos a=2R\cdot\cos a.$$

Альтернативное решение через центральный угол и формулу хорды

• Вписанный угол $\angle ACB$ опирается на дугу $AB$, а $\angle ABC=90^\circ$, значит сумма углов треугольника:

$$\angle A + \angle B + \angle C = 180^\circ \quad\Rightarrow\quad a + 90^\circ + \angle C = 180^\circ,$$ $$\angle C = 90^\circ — a.$$

• Центральный угол $\angle AOB$, опирающийся на ту же дугу $AB$, вдвое больше вписанного:

$$\angle AOB = 2\angle ACB = 2(90^\circ — a).$$

• Длина хорды по центральному углу $\varphi=\angle AOB$:

$$AB = 2R\sin\frac{\varphi}{2} = 2R\sin\!\big(90^\circ — a\big) = 2R\cos a.$$

Проверка размерности, пределов и здравого смысла

• Максимальная возможная хорда — диаметр: $AB\le 2R$. Формула даёт $AB=2R\cos a\le 2R$ (так как $\cos a\le 1$) — ок.
• При $a\to 0^\circ$: $\cos a\to 1\Rightarrow AB\to 2R$ — хорда стремится к диаметру, логично.
• При $a\to 90^\circ$: $\cos a\to 0\Rightarrow AB\to 0$ — точка $B$ «подходит» к $A$, хорда вырождается — тоже логично.

Ответ

$$\boxed{\,AB=2R\cos a\,}.$$