ГДЗ 10-11 Класс Номер 8.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Докажите, что площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

Доказать, что площадь выпуклого четырехугольника равна половине произведения длин его диагоналей на синус угла между ними.

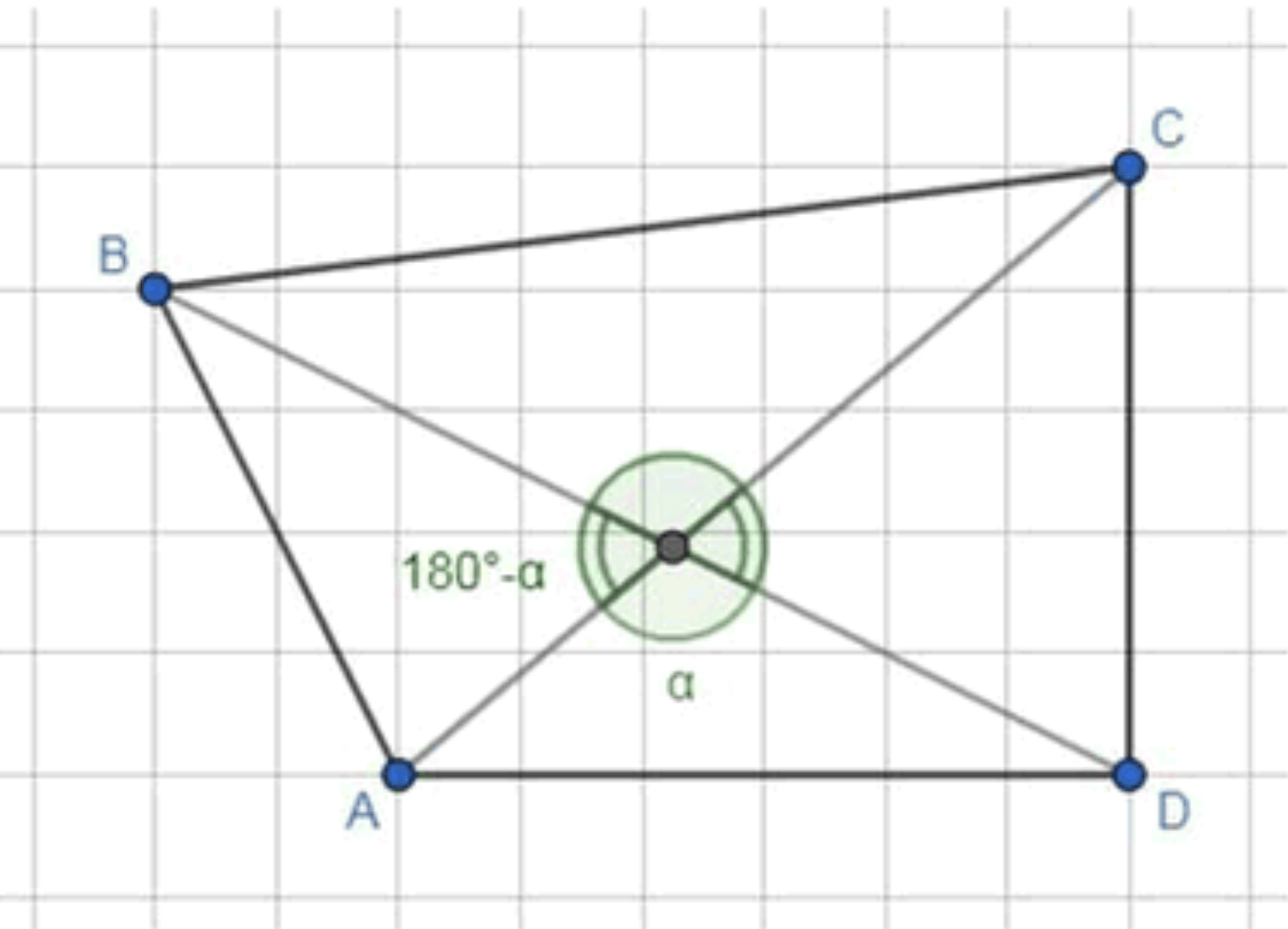
1) Пусть дан четырехугольник $ABCD$, диагонали $AC$ и $BD$ которого пересекаются в точке $O$, а острый угол $AOD$ между ними равен $\alpha$:

2) Выведем тождество:

$$\sin(180^\circ — \alpha) = \sin(\pi — \alpha) = -\sin(-\alpha) = \sin \alpha;$$

3) По теореме о площади треугольника:

$$S_{AOB} = \frac{1}{2} \cdot AO \cdot BO \cdot \sin(180^\circ — \alpha) = \frac{1}{2} AO \cdot BO \cdot \sin \alpha;$$ $$S_{BOC} = \frac{1}{2} \cdot BO \cdot OC \cdot \sin \alpha;$$ $$S_{COD} = \frac{1}{2} \cdot CO \cdot OD \cdot \sin(180^\circ — \alpha) = \frac{1}{2} CO \cdot OD \cdot \sin \alpha;$$ $$S_{AOD} = \frac{1}{2} \cdot DO \cdot AO \cdot \sin \alpha;$$

4) Площадь четырехугольника:

$$S_{ABCD} = S_{AOB} + S_{BOC} + S_{COD} + S_{AOD};$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot (AO \cdot BO + BO \cdot OC + CO \cdot OD + DO \cdot AO);$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot (BO(AO + OC) + OD(AO + OC));$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot (AO + OC) \cdot (BO + OD);$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot AC \cdot BD;$$

Что и требовалось доказать.

Доказать, что для любого выпуклого четырёхугольника площадь

$$S_{ABCD}=\frac12\cdot AC\cdot BD\cdot\sin\varphi,$$

где $AC$ и $BD$ — длины диагоналей, а $\varphi$ — угол между ними.

1) Подготовка: формула площади треугольника через две стороны и угол

Для треугольника со сторонами $p$ и $q$, заключающими угол $\gamma$, высота к стороне $p$ равна $q\sin\gamma$. Поэтому

$$S_{\triangle}=\frac12\cdot p\cdot (q\sin\gamma)=\frac12\,pq\sin\gamma.$$

Это будем применять многократно.

2) Конфигурация и обозначения

Пусть $ABCD$ — выпуклый четырёхугольник. Его диагонали $AC$ и $BD$ пересекаются в точке $O$. Угол между прямыми $AC$ и $BD$ обозначим $\alpha$ и считаем $0^\circ<\alpha<180^\circ$. (Выпуклость гарантирует, что диагонали пересекаются внутри фигуры и $\alpha\neq 0^\circ,180^\circ$.)

Замечание об углах при пересечении двух прямых:

• соседние углы дополняют друг друга до $180^\circ$;
• вертикальные углы равны.
  Значит, если $\angle AOD=\alpha$, то $\angle AOB=\angle COD=180^\circ-\alpha$, а $\angle BOC=\angle AOD=\alpha$.

Также используем тождество

$$\sin(180^\circ-\alpha)=\sin\alpha,$$

так что синус у «дополнительного» угла совпадает.

3) Разбиваем площадь на четыре треугольника

Четырёхугольник разбит диагоналями на четыре треугольника: $AOB$, $BOC$, $COD$, $DOA$. Их площади (по формуле из п.1) равны:

• Для $\triangle AOB$ стороны, заключающие угол при $O$: $AO$ и $BO$; угол $=180^\circ-\alpha$:

$$S_{AOB}=\frac12\cdot AO\cdot BO\cdot \sin(180^\circ-\alpha)=\frac12\,AO\,BO\,\sin\alpha.$$

• Для $\triangle BOC$ стороны $BO$ и $CO$; угол $=\alpha$:

$$S_{BOC}=\frac12\cdot BO\cdot CO\cdot \sin\alpha.$$

• Для $\triangle COD$ стороны $CO$ и $DO$; угол $=180^\circ-\alpha$:

$$S_{COD}=\frac12\cdot CO\cdot DO\cdot \sin(180^\circ-\alpha)=\frac12\,CO\,DO\,\sin\alpha.$$

• Для $\triangle DOA$ стороны $DO$ и $AO$; угол $=\alpha$:

$$S_{AOD}=\frac12\cdot DO\cdot AO\cdot \sin\alpha.$$

Так как четырёхугольник выпуклый, суммарная площадь равна сумме площадей этих четырёх треугольников:

$$S_{ABCD}=S_{AOB}+S_{BOC}+S_{COD}+S_{AOD}.$$

4) Алгебраическое суммирование и факторизация

Подставим выражения:

$$\begin{aligned} S_{ABCD} &=\frac12\sin\alpha\bigl(AO\cdot BO+BO\cdot CO+CO\cdot DO+DO\cdot AO\bigr)\\[4pt] &=\frac12\sin\alpha\bigl(BO(AO+CO)+DO(CO+AO)\bigr)\\[4pt] &=\frac12\sin\alpha\,(AO+CO)\,(BO+DO). \end{aligned}$$

Но $AO+OC=AC$ и $BO+OD=BD$ (по определению точка $O$ делит диагонали на отрезки). Следовательно,

$$S_{ABCD}=\frac12\,\sin\alpha\cdot AC\cdot BD,$$

что и требовалось.

5) Почему не важно, какой угол между диагоналями брать

Из п.2: у пересечения диагоналей есть два различных угла $\alpha$ и $180^\circ-\alpha$. Их синусы равны, поэтому формула корректна для «любого» угла между диагоналями: результат один и тот же.

6) Границы применимости и частные случаи

• Выпуклость нужна, чтобы площадь четырёхугольника была просто суммой четырёх треугольников (без «вычитаний»).
• Если $\alpha=90^\circ$ (диагонали перпендикулярны), то $S=\tfrac12\,AC\,BD$ — известная формула, например для ромба и кайта.
• Для прямоугольника со сторонами $a,b$: $AC=BD=\sqrt{a^2+b^2}$, $\sin\alpha=\dfrac{2ab}{a^2+b^2}$; тогда

$$S=\frac12(a^2+b^2)\cdot\frac{2ab}{a^2+b^2}=ab,$$

что совпадает с привычной формулой.

7) Короткое альтернативное доказательство (векторное)

Рассмотрим диагонали как векторы $\vec d_1=\overrightarrow{AC}$ и $\vec d_2=\overrightarrow{BD}$. Площадь выпуклого четырёхугольника равна половине модуля «векторного произведения» диагоналей в плоскости:

$$S=\frac12\,\lvert \vec d_1\times \vec d_2\rvert=\frac12\,\lvert \vec d_1\rvert\,\lvert \vec d_2\rvert\,\sin\varphi =\frac12\,AC\cdot BD\cdot\sin\varphi,$$

где $\varphi$ — угол между диагоналями. Это ровно та же формула.

Что и требовалось доказать.