ГДЗ 10-11 Класс Номер 8.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

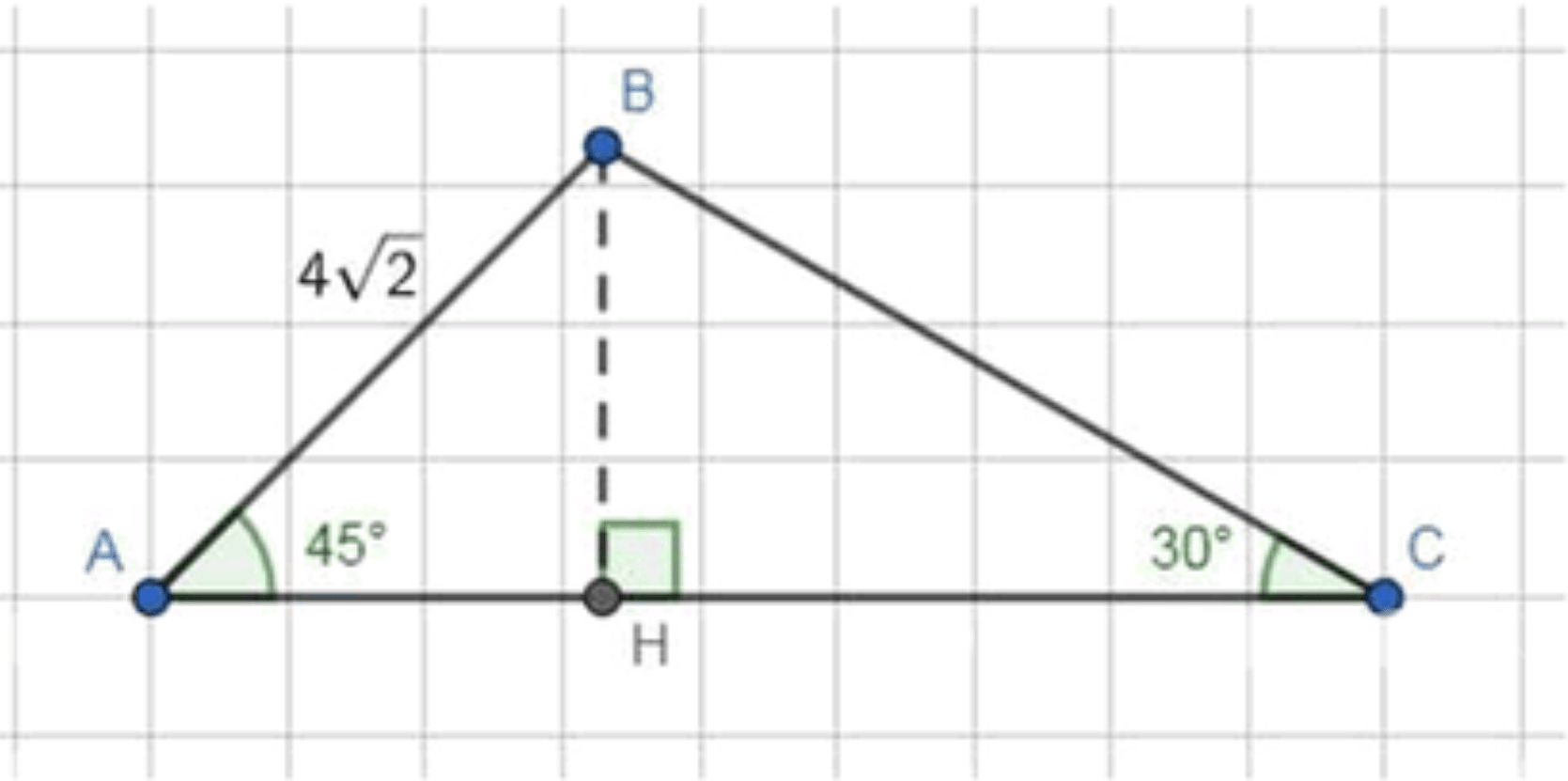
В треугольнике АВС известно, что АВ = $4\sqrt{2}$ см, угол A = ${45}^{\circ }$, угол C = ${30}^{\circ }$. Найдите ВС, АС и площадь треугольника АВС.

В ΔABC известно, что $AB=4\sqrt{2}$ см, $\mathrm{\angle }A={45}^{\circ }$, $\mathrm{\angle }C={30}^{\circ }$.

Найти $BC$, $AC$ и площадь $\mathrm{\Delta }ABC$.

Отобразим условие задачи:

Радианные меры углов:

$$\mathrm{\angle }A={45}^{\circ }=\frac{\pi \cdot 45}{180}=\frac{9\pi }{36}=\frac{\pi }{4};$$$$\mathrm{\angle }C={30}^{\circ }=\frac{\pi \cdot 30}{180}=\frac{3\pi }{18}=\frac{\pi }{6};$$

По теореме синусов:

$$\frac{BC}{\sin \mathrm{\angle }A}=\frac{AB}{\sin \mathrm{\angle }C};$$$$BC=\frac{\sin \mathrm{\angle }A}{\sin \mathrm{\angle }C}\cdot AB=\frac{\sin \frac{\pi }{4}}{\sin \frac{\pi }{6}}\cdot 4\sqrt{2}=(\frac{\sqrt{2}}{2}:\frac{1}{2})\cdot 4\sqrt{2}=8\text{ см};$$

Рассмотрим прямоугольный ΔCBH:

$$\sin \mathrm{\angle }C=\frac{BH}{BC}\Rightarrow BH=BC\cdot \sin \mathrm{\angle }C=8\cdot \sin \frac{\pi }{6}=8\cdot \frac{1}{2}=4\text{ см};$$$$\cos \mathrm{\angle }C=\frac{CH}{BC}\Rightarrow CH=BC\cdot \cos \mathrm{\angle }C=8\cdot \cos \frac{\pi }{6}=8\cdot \frac{\sqrt{3}}{2}=4\sqrt{3}\text{ см};$$

Рассмотрим прямоугольный ΔABH:

$$\cos \mathrm{\angle }A=\frac{AH}{AB};$$$$AH=AB\cdot \cos \mathrm{\angle }A=4\sqrt{2}\cdot \cos \frac{\pi }{4}=4\sqrt{2}\cdot \frac{\sqrt{2}}{2}=2\cdot 2=4\text{ см};$$

Длина стороны AC:

$$AC=AH+HC=4+4\sqrt{3}=4(1+\sqrt{3})\text{ см};$$

Площадь треугольника ABC:

$$S_{\mathrm{\Delta }ABC}=\frac{1}{2}\cdot AC\cdot BH=\frac{1}{2}\cdot 4(1+\sqrt{3})\cdot 4=8(1+\sqrt{3}){\text{ см}}^2;$$

Ответ: $BC=8$ см; $AC=4(1+\sqrt{3})$ см; $S_{\mathrm{\Delta }ABC}=8(1+\sqrt{3})$ см².

Дано

• Треугольник $\mathrm{△}ABC$.
• $AB=4\sqrt{2}\text{см}$.
• $\mathrm{\angle }A={45}^{\circ }$.
• $\mathrm{\angle }C={30}^{\circ }$.

Найти: $BC$, $AC$ и $S_{\mathrm{△}ABC}$.

Для удобства используем стандартные обозначения сторон:
$a=BC$ (напротив угла $A$), $b=AC$ (напротив угла $B$), $c=AB$ (напротив угла $C$).

1) Угол $B$ по сумме углов треугольника

$$\mathrm{\angle }B={180}^{\circ }-\mathrm{\angle }A-\mathrm{\angle }C={180}^{\circ }-{45}^{\circ }-{30}^{\circ }={105}^{\circ }\mathrm{.}$$

Промежуточный вывод: углы $A={45}^{\circ }$, $B={105}^{\circ }$, $C={30}^{\circ }$.

2) Тригонометрические значения (точные)

$$\sin {45}^{\circ }=\frac{\sqrt{2}}{2},\sin {30}^{\circ }=\frac{1}{2}\mathrm{.}$$

$$\sin {105}^{\circ }=\sin ({60}^{\circ }+{45}^{\circ })=\sin {60}^{\circ }\cos {45}^{\circ }+\cos {60}^{\circ }\sin {45}^{\circ }=$$

$$=\frac{\sqrt{3}}{2}\cdot \frac{\sqrt{2}}{2}+\frac{1}{2}\cdot \frac{\sqrt{2}}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}\mathrm{.}$$

3) Закон синусов (главный расчёт)

Закон синусов:

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\mathrm{.}$$

Нам дано $c=AB=4\sqrt{2}$, $A={45}^{\circ }$, $B={105}^{\circ }$, $C={30}^{\circ }$.

3.1) Сторона $a=BC$

$$a=\frac{\sin A}{\sin C}c=\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}\cdot 4\sqrt{2}=(\frac{\sqrt{2}}{2}\cdot 2)\cdot 4\sqrt{2}=\sqrt{2}\cdot 4\sqrt{2}=4\cdot 2=8\text{ см}\mathrm{.}$$

3.2) Сторона $b=AC$

$$b=\frac{\sin B}{\sin C}c=\frac{\frac{\sqrt{6}+\sqrt{2}}{4}}{\frac{1}{2}}\cdot 4\sqrt{2}=\left(\frac{\sqrt{6}+\sqrt{2}}{2}\right)\cdot 4\sqrt{2}=2\sqrt{2}(\sqrt{6}+\sqrt{2})=$$

$$=2\sqrt{12}+2\cdot 2=4\sqrt{3}+4=4(1+\sqrt{3})\text{ см}\mathrm{.}$$

Промежуточный вывод: $BC=8$ см, $AC=4(1+\sqrt{3})$ см.

4) Альтернативный вывод через высоту и проекции

Опустим из $B$ перпендикуляр $BH$ на $AC$ (точка $H$ на $AC$).

В прямоугольном $\mathrm{△}CBH$ (угол при $C$ равен ${30}^{\circ }$, гипотенуза $BC=a=8$):

$$BH=BC\cdot \sin C=8\cdot \frac{1}{2}=4\text{ см},$$$$CH=BC\cdot \cos C=8\cdot \frac{\sqrt{3}}{2}=4\sqrt{3}\text{ см}\mathrm{.}$$

В прямоугольном $\mathrm{△}ABH$ (угол при $A$ равен ${45}^{\circ }$, гипотенуза $AB=c=4\sqrt{2}$):

$$AH=AB\cdot \cos A=4\sqrt{2}\cdot \frac{\sqrt{2}}{2}=4\text{ см}\mathrm{.}$$

Тогда

$$AC=AH+HC=4+4\sqrt{3}=4(1+\sqrt{3})\text{ см},$$

а $BC$ уже найден как 8 см — всё согласуется с п.3.

5) Площадь треугольника (несколько способов)

5.1) Через две стороны и синус угла между ними

Угол между сторонами $AC$ и $BC$ — это $\mathrm{\angle }C={30}^{\circ }$:

$$S=\frac{1}{2}AC\cdot BC\cdot \sin C=\frac{1}{2}\cdot 4(1+\sqrt{3})\cdot 8\cdot \frac{1}{2}=8(1+\sqrt{3}){\text{см}}^2\mathrm{.}$$

5.2) Через высоту (на ту же базу $AC$)

$$S=\frac{1}{2}\cdot AC\cdot BH=\frac{1}{2}\cdot 4(1+\sqrt{3})\cdot 4=8(1+\sqrt{3}){\text{см}}^2\mathrm{.}$$

5.3) Ещё одна быстрая проверка: через $AB$, $AC$ и $\sin A$

Между $AB$ и $AC$ угол $A={45}^{\circ }$:

$$S=\frac{1}{2}AB\cdot AC\cdot \sin A=\frac{1}{2}\cdot 4\sqrt{2}\cdot 4(1+\sqrt{3})\cdot \frac{\sqrt{2}}{2}\mathrm{.}$$

Поскольку $\sqrt{2}\cdot \frac{\sqrt{2}}{2}=1$, получаем

$$S=\frac{1}{2}\cdot 4\cdot 4(1+\sqrt{3})=8(1+\sqrt{3}){\text{см}}^2\mathrm{.}$$

Все три способа дают один и тот же ответ.

6) Контрольные проверки

6.1) Сравнение сторон и углов

• Наибольший угол $B={105}^{\circ }$ ⇒ напротив него наибольшая сторона $AC$. Действительно, $AC=4(1+\sqrt{3})\approx \mathrm{10,928}$ см — самая длинная.
• Наименьший угол $C={30}^{\circ }$ ⇒ напротив него наименьшая сторона $AB=4\sqrt{2}\approx \mathrm{5,657}$ см — самая короткая.
• Оставшаяся сторона $BC=8$ см — средняя. Логика «больше угол — больше сторона» соблюдается.

6.2) Числовая проверка площадей

$$8(1+\sqrt{3})\approx 8(1+\mathrm{1,73205})\approx 8\cdot \mathrm{2,73205}\approx \mathrm{21,856}{\text{см}}^2\mathrm{.}$$

Если применить формулу Герона численно с $a=8$, $b\approx \mathrm{10,928}$, $c\approx \mathrm{5,657}$, получится та же величина (около $\mathrm{21,86}{\text{см}}^2$) — совпадает.

6.3) Маленькая «изюминка» про описанную окружность

По закону синусов $2R={\displaystyle \frac{c}{\sin C}}\Rightarrow R={\displaystyle \frac{c}{2\sin C}}$.
Здесь $c=4\sqrt{2}$, $\sin C=\frac{1}{2}$:

$$R=\frac{4\sqrt{2}}{2\cdot \frac{1}{2}}=4\sqrt{2}\mathrm{.}$$

То есть радиус описанной окружности равен… $AB$. Это редкая, но корректная ситуация: так как $C={30}^{\circ }$, сторона напротив него равна $2R\sin {30}^{\circ }=R$.

Итоговый ответ

$$\boxed{{\displaystyle BC=8\text{ см},AC=4(1+\sqrt{3})\text{ см},S_{\mathrm{△}ABC}=8(1+\sqrt{3}){\text{см}}^2}}$$