ГДЗ по Алгебре 10 Класс Номер 1.16 Профильный Уровень Мордкович — Подробные Ответы

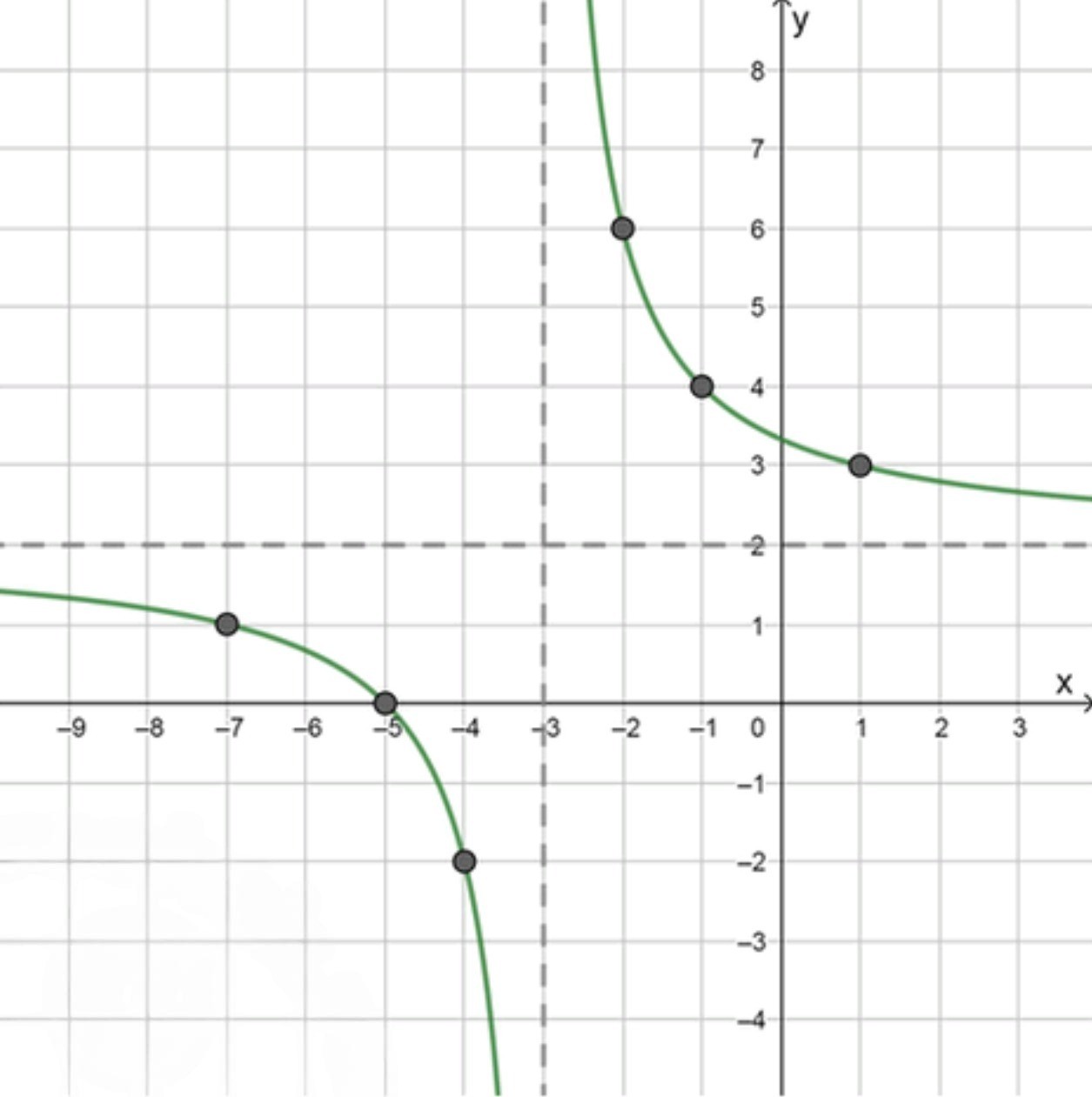
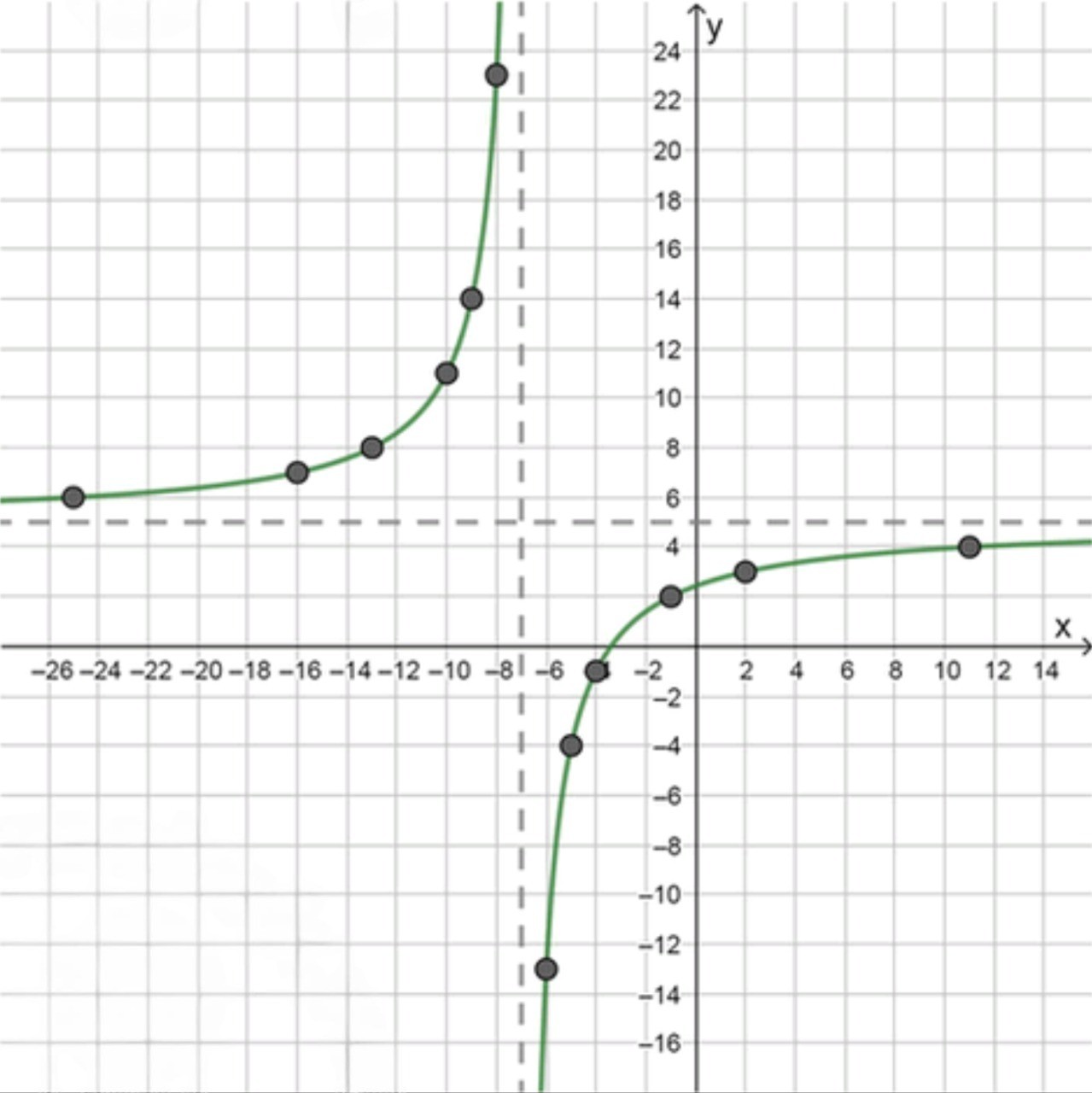
Ha графике заданной функции найдите все точки, обе координаты которых — целые числа:

а) $y=2+\frac{4}{x+3}$;

б) $y=\frac{5x+17}{x+7}=\frac{5x+35-18}{x+7}=5-\frac{18}{x+7}$

На графике заданной функции найти все точки, обе координаты которых — целые числа;

а) $y=2+\frac{4}{x+3}$;

Уравнения асимптот гиперболы:

• $x=-3$
• $y=2$

Делители числа четыре: $1;2;4$;

• $x+3=1$, отсюда $x=-2$;
• $x+3=2$, отсюда $x=-1$;
• $x+3=4$, отсюда $x=1$;

Координаты некоторых точек:

График функции:

б) $y=\frac{5x+17}{x+7}=\frac{5x+35-18}{x+7}=5-\frac{18}{x+7}$;

Уравнения асимптот гиперболы:

• $x=-7$
• $y=5$

Делители числа восемнадцать: $1;2;3;6;9;18$;

• $x+7=1$, отсюда $x=-6$;
• $x+7=2$, отсюда $x=-5$;
• $x+7=3$, отсюда $x=-4$;
• $x+7=6$, отсюда $x=-1$;
• $x+7=9$, отсюда $x=2$;
• $x+7=18$, отсюда $x=11$;

Координаты некоторых точек:

График функции:

а) $y=2+\frac{4}{x+3}$

Шаг 1: Асимптоты гиперболы

График функции $y=2+\frac{4}{x+3}$ представляет собой гиперболу, у которой есть вертикальная и горизонтальная асимптоты.

• Горизонтальная асимптота: Она получается, если рассматривать предел при $x\to \mathrm{\infty }$ или $x\to -\mathrm{\infty }$. В этом случае $\frac{4}{x+3}\to 0$, и остается только $y=2$. Поэтому горизонтальная асимптота: $y=2$.
• Вертикальная асимптота: Вертикальная асимптота возникает, когда знаменатель дроби стремится к нулю, то есть $x+3=0$, что дает $x=-3$. Поэтому вертикальная асимптота: $x=-3$.

Шаг 2: Найдем значения $x$, при которых $\frac{4}{x+3}$ целое число

Чтобы $y=2+\frac{4}{x+3}$ было целым числом, дробь $\frac{4}{x+3}$ должна быть целым числом. Это возможно, если $x+3$ — делитель числа 4. Разложим 4 на множители:

$$4=2^2$$

Делители числа 4: $1,2,4$, а значит:

• $x+3=1$, отсюда $x=-2$;
• $x+3=2$, отсюда $x=-1$;
• $x+3=4$, отсюда $x=1$.

Таким образом, возможные значения для $x$ — это $x=-2$, $x=-1$, $x=1$.

Шаг 3: Найдем соответствующие значения $y$ для этих $x$

Для $x=-2$:

$$y=2+\frac{4}{-2+3}=2+\frac{4}{1}=2+4=6$$

Таким образом, точка $(-2,6)$.

Для $x=-1$:

$$y=2+\frac{4}{-1+3}=2+\frac{4}{2}=2+2=4$$

Таким образом, точка $(-1,4)$.

Для $x=1$:

$$y=2+\frac{4}{1+3}=2+\frac{4}{4}=2+1=3$$

Таким образом, точка $(1,3)$.

Шаг 4: Ответ для пункта а

Таким образом, все точки, где обе координаты — целые числа, для функции $y=2+\frac{4}{x+3}$, это:

$$(-2,6),(-1,4),(1,3)$$

б) $y=\frac{5x+17}{x+7}=\frac{5x+35-18}{x+7}=5-\frac{18}{x+7}$

Шаг 1: Асимптоты гиперболы

Для функции $y=\frac{5x+17}{x+7}$, у нас также гипербола с двумя асимптотами:

• Горизонтальная асимптота: Рассмотрим предел при $x\to \mathrm{\infty }$ или $x\to -\mathrm{\infty }$. Тогда дробь $\frac{18}{x+7}\to 0$, и остается только $y=5$. Это означает, что горизонтальная асимптота: $y=5$.
• Вертикальная асимптота: Вертикальная асимптота возникает, когда $x+7=0$, то есть $x=-7$. Это означает, что вертикальная асимптота: $x=-7$.

Шаг 2: Найдем значения $x$, при которых $\frac{18}{x+7}$ целое число

Для того, чтобы выражение $5-\frac{18}{x+7}$ было целым числом, дробь $\frac{18}{x+7}$ должна быть целым числом. Это возможно, если $x+7$ — делитель числа 18. Разложим 18 на множители:

$$18=2\times 3^2$$

Делители числа 18: $1,2,3,6,9,18$. Следовательно, возможные значения $x+7$ — это:

• $x+7=1$, отсюда $x=-6$;
• $x+7=2$, отсюда $x=-5$;
• $x+7=3$, отсюда $x=-4$;
• $x+7=6$, отсюда $x=-1$;
• $x+7=9$, отсюда $x=2$;
• $x+7=18$, отсюда $x=11$.

Шаг 3: Найдем соответствующие значения $y$ для этих $x$

Для $x=-6$:

$$y=5-\frac{18}{-6+7}=5-\frac{18}{1}=5-18=-13$$

Таким образом, точка $(-6,-13)$.

Для $x=-5$:

$$y=5-\frac{18}{-5+7}=5-\frac{18}{2}=5-9=-4$$

Таким образом, точка $(-5,-4)$.

Для $x=-4$:

$$y=5-\frac{18}{-4+7}=5-\frac{18}{3}=5-6=-1$$

Таким образом, точка $(-4,-1)$.

Для $x=-1$:

$$y=5-\frac{18}{-1+7}=5-\frac{18}{6}=5-3=2$$

Таким образом, точка $(-1,2)$.

Для $x=2$:

$$y=5-\frac{18}{2+7}=5-\frac{18}{9}=5-2=3$$

Таким образом, точка $(2,3)$.

Для $x=11$:

$$y=5-\frac{18}{11+7}=5-\frac{18}{18}=5-1=4$$

Таким образом, точка $(11,4)$.

Шаг 4: Ответ для пункта б

Таким образом, все точки, где обе координаты — целые числа, для функции $y=\frac{5x+17}{x+7}$, это:

$$(-6,-13),(-5,-4),(-4,-1),(-1,2),(2,3),(11,4)$$

Итоговое решение:

1. Для пункта а: $(-2,6),(-1,4),(1,3)$
2. Для пункта б: $(-6,-13),(-5,-4),(-4,-1),(-1,2),(2,3),(11,4)$