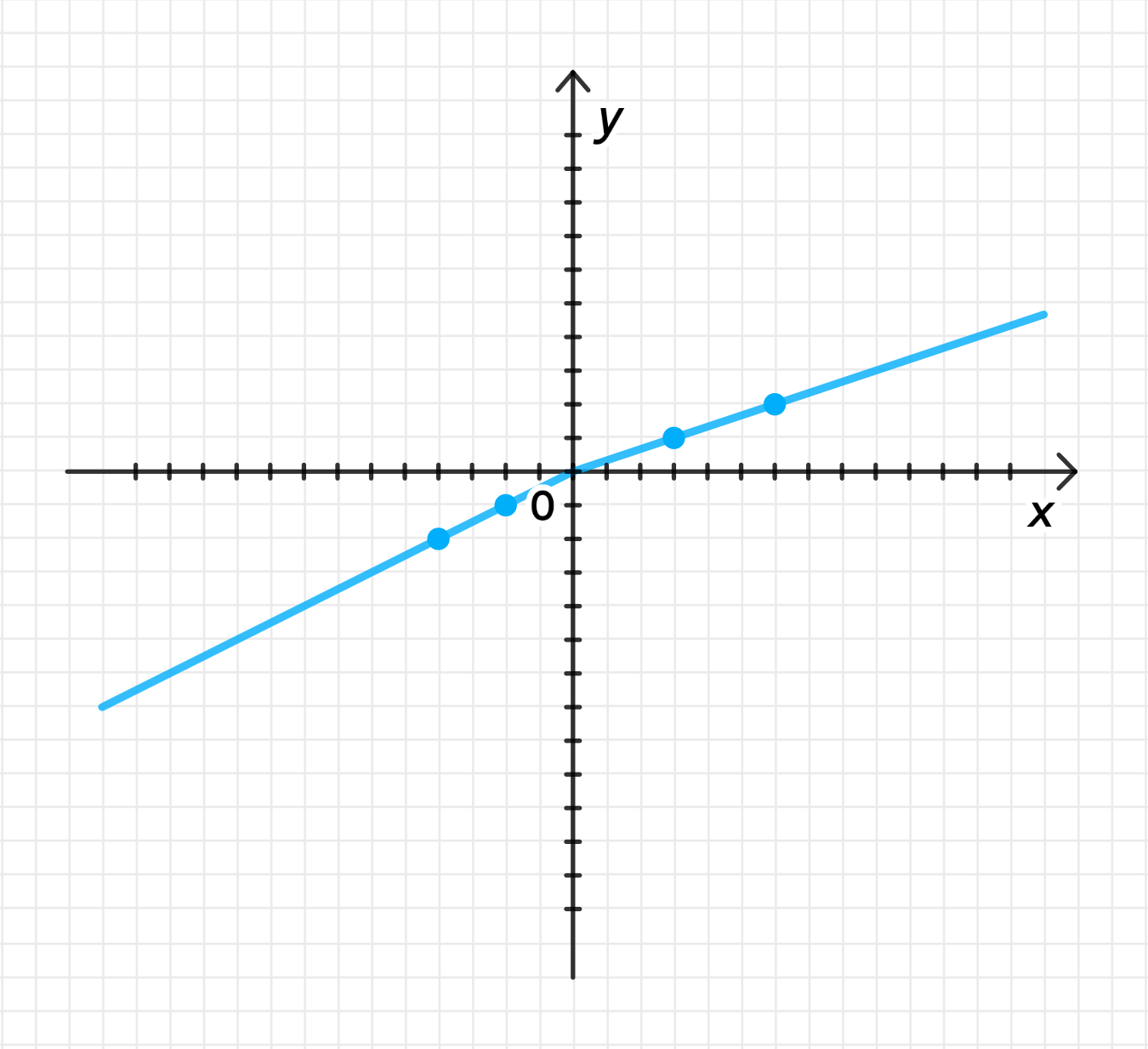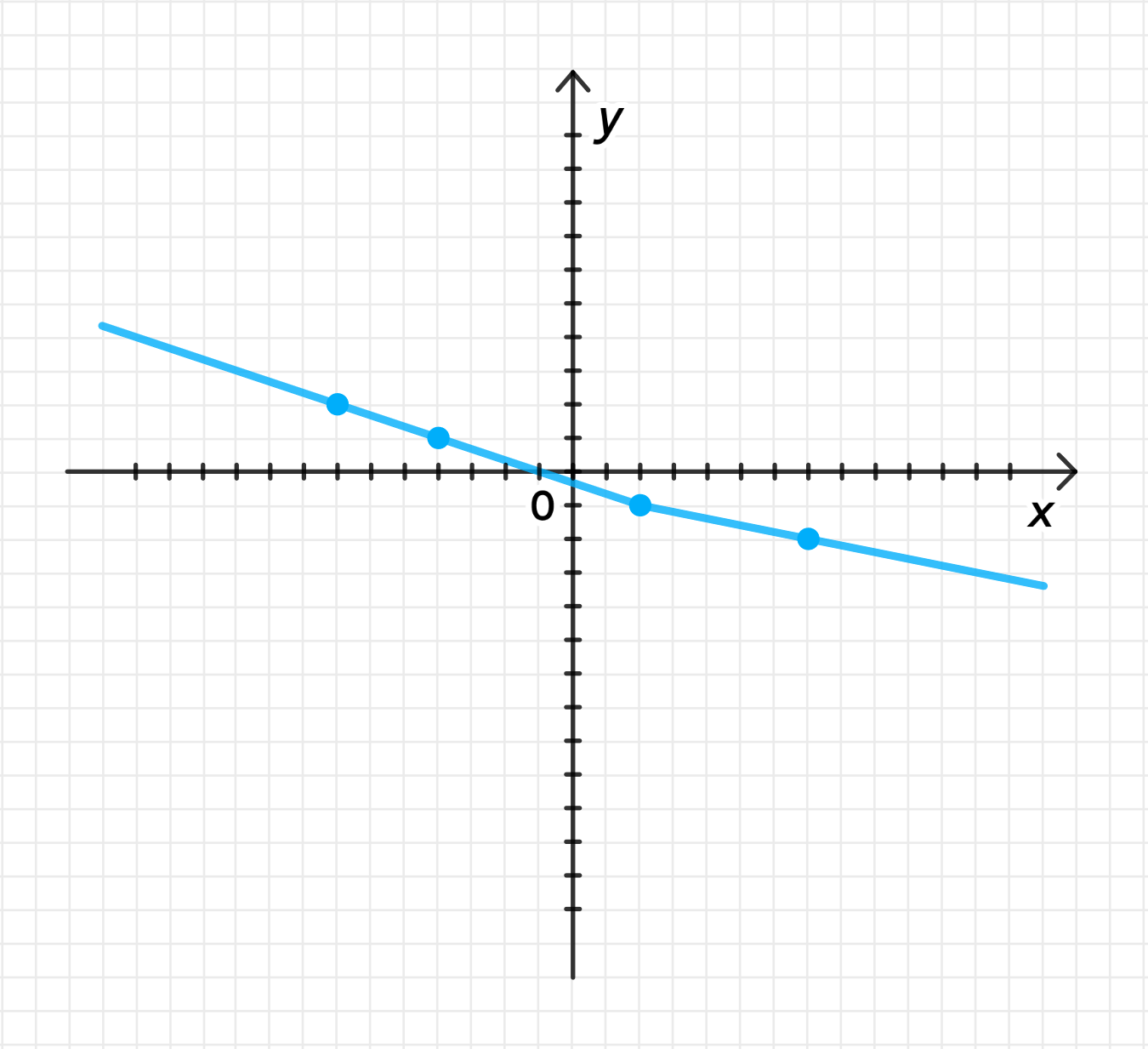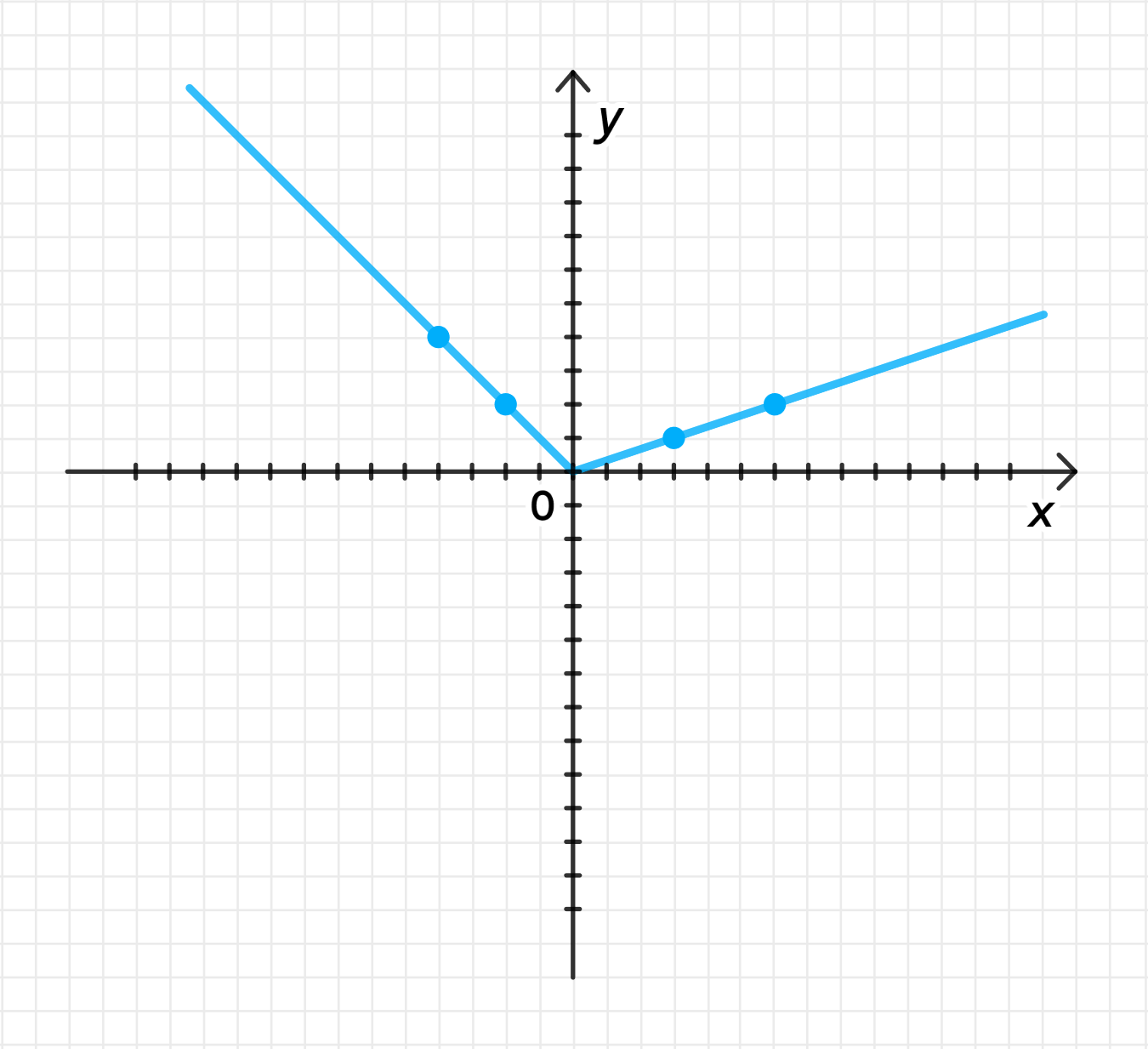ГДЗ по Алгебре 10 Класс Номер 10.12 Профильный Уровень Мордкович — Подробные Ответы

Задайте функцию, обратную данной; постройте ее график:

а) $y=\{\begin{array}{ll}2x,& \text{если }x\le 0\\ 3x,& \text{если }x>0\end{array}$

б) $y=\{\begin{array}{ll}-5x-3,& \text{если }x\le -1\\ -1-3x,& \text{если }x>-1\end{array}$

в) $y=\{\begin{array}{ll}-x,& \text{если }x<0\\ -3x,& \text{если }x\ge 0\end{array}$

г) $y=\{\begin{array}{ll}2x+1,& \text{если }x\le 2\\ \frac{1}{2}x+4,& \text{если }x\ge 2\end{array}$$\begin{array}{l}\end{array}$$\begin{array}{l}\end{array}$

а) $y = \begin{cases} 2x, & \text{если } x \leq 0; \\ 3x, & \text{если } x > 0; \end{cases}$

Если $x \leq 0$, тогда:

$$2x \leq 0 \quad \Rightarrow \quad y \leq 0;$$ $$x = 2y;$$ $$y = 0.5x;$$

Если $x > 0$, тогда:

$$3x > 0 \quad \Rightarrow \quad y > 0;$$ $$x = 3y;$$ $$y = \frac{1}{3}x;$$

Функция, обратная данной:

$$y = \begin{cases} 0.5x, & \text{если } x \leq 0; \\ \frac{1}{3}x, & \text{если } x > 0; \end{cases}$$

График обратной функции:

б) $y = \begin{cases} -5x — 3, & \text{если } x \leq -1; \\ -1 — 3x, & \text{если } x > -1; \end{cases}$

Если $x \leq -1$, тогда:

$$-5x \geq 5 \quad \Rightarrow \quad -5x — 3 \geq 2 \quad \Rightarrow \quad y \geq 2;$$ $$x = -5y — 3;$$ $$5y = -x — 3;$$ $$y = -\frac{x + 3}{5};$$

Если $x > -1$, тогда:

$$-3x < 3 \quad \Rightarrow \quad -1 — 3x < 2 \quad \Rightarrow \quad y < 2;$$ $$x = -1 — 3y;$$ $$3y = -x — 1;$$ $$y = -\frac{x + 1}{3};$$

Функция, обратная данной:

$$y = \begin{cases} -\frac{x + 3}{5}, & \text{если } x \geq 2; \\ -\frac{x + 1}{3}, & \text{если } x < 2; \end{cases}$$

График обратной функции:

в) $y = \begin{cases} -x, & \text{если } x < 0; \\ -3x, & \text{если } x \geq 0; \end{cases}$

Если $x < 0$, тогда:

$$-x > 0 \quad \Rightarrow \quad y > 0;$$ $$x = -y;$$ $$y = -x;$$

Если $x \geq 0$, тогда:

$$-3x \leq 0 \quad \Rightarrow \quad y \leq 0;$$ $$x = -3y;$$ $$y = -\frac{1}{3}x;$$

Функция, обратная данной:

$$y = \begin{cases} -\frac{1}{3}x, & \text{если } x \leq 0; \\ -x, & \text{если } x > 0; \end{cases}$$

График обратной функции:

г) $y = \begin{cases} 2x + 1, & \text{если } x \leq 2; \\ \frac{1}{2}x + 4, & \text{если } x \geq 2; \end{cases}$

Если $x \leq 2$, тогда:

$$2x \leq 4 \quad \Rightarrow \quad 2x + 1 \leq 5 \quad \Rightarrow \quad y \leq 5;$$ $$x = 2y + 1;$$ $$2y = x — 1;$$ $$y = 0.5(x — 1);$$

Если $x \geq 2$, тогда:

$$\frac{1}{2}x \geq 1 \quad \Rightarrow \quad \frac{1}{2}x + 4 \geq 5 \quad \Rightarrow \quad y \geq 5;$$ $$x = \frac{1}{2}y + 4;$$ $$2x = y + 8;$$ $$y = 2x — 8;$$

Функция, обратная данной:

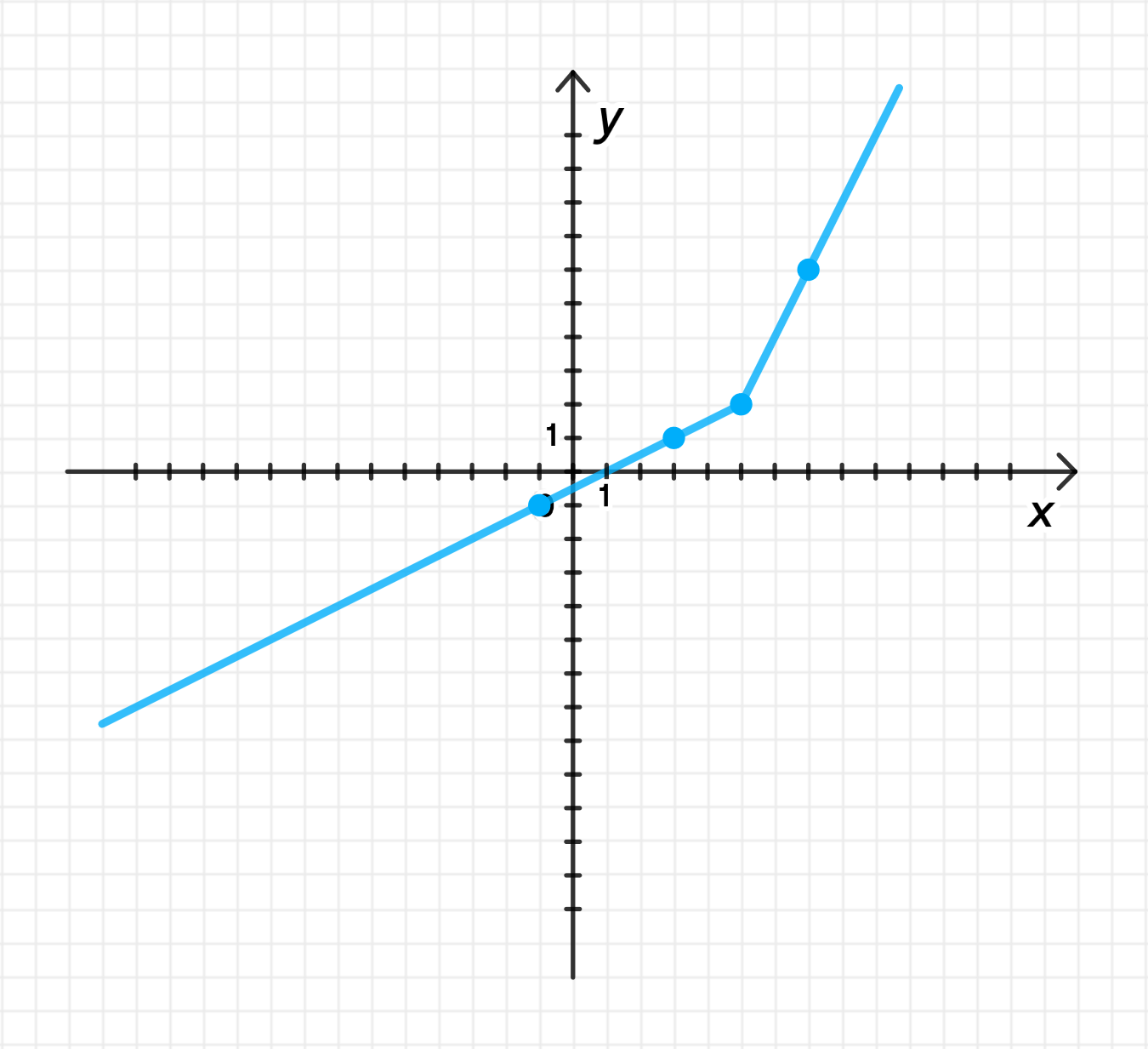
$$y = \begin{cases} 0.5(x — 1), & \text{если } x \leq 5; \\ 2x — 8, & \text{если } x \geq 5; \end{cases}$$

График обратной функции:

а) Функция:

$$y = \begin{cases} 2x, & \text{если } x \leq 0; \\ 3x, & \text{если } x > 0. \end{cases}$$

Для $x \leq 0$:

Мы знаем, что $y = 2x$. Рассмотрим, что происходит при $x \leq 0$:

$$2x \leq 0 \quad \Rightarrow \quad y \leq 0.$$

Далее, выражение для $x$ через $y$ (обратная зависимость):

$$x = \frac{y}{2}.$$

Это выражение будет работать при $y \leq 0$, потому что для $x \leq 0$ функция $y = 2x$ всегда принимает отрицательные или нулевые значения.

Для $x > 0$:

Мы знаем, что $y = 3x$. Рассмотрим, что происходит при $x > 0$:

$$3x > 0 \quad \Rightarrow \quad y > 0.$$

Выражение для $x$ через $y$ (обратная зависимость):

$$x = \frac{y}{3}.$$

Это выражение будет работать при $y > 0$, потому что для $x > 0$ функция $y = 3x$ всегда принимает положительные значения.

Обратная функция:

Теперь, учитывая вышеизложенное, можем записать обратную функцию:

$$y = \begin{cases} 0.5x, & \text{если } x \leq 0; \\ \frac{1}{3}x, & \text{если } x > 0. \end{cases}$$

Функция для $y$ для $x \leq 0$ будет $y = 0.5x$, а для $x > 0$ — $y = \frac{1}{3}x$.

Таблица значений:

Рассмотрим таблицу значений для функции и её обратной функции:

• При $x = -2$, $y = 2(-2) = -4$.
• При $x = 0$, $y = 2(0) = 0$.
• При $x = 3$, $y = 3(3) = 9$.

График обратной функции:

б) Функция:

$$y = \begin{cases} -5x — 3, & \text{если } x \leq -1; \\ -1 — 3x, & \text{если } x > -1. \end{cases}$$

Для $x \leq -1$:

При $x \leq -1$, $y = -5x — 3$. Рассмотрим неравенства для $y$:

$$-5x — 3 \geq 2 \quad \Rightarrow \quad y \geq 2.$$

Рассмотрим выражение для $x$:

$$x = -5y — 3 \quad \Rightarrow \quad y = -\frac{x + 3}{5}.$$

Для $x > -1$:

При $x > -1$, $y = -1 — 3x$. Рассмотрим неравенства для $y$:

$$-3x — 1 < 2 \quad \Rightarrow \quad y < 2.$$

Рассмотрим выражение для $x$:

$$x = -1 — 3y \quad \Rightarrow \quad y = -\frac{x + 1}{3}.$$

Обратная функция:

Теперь, учитывая вышеизложенное, можем записать обратную функцию:

$$y = \begin{cases} -\frac{x + 3}{5}, & \text{если } x \geq 2; \\ -\frac{x + 1}{3}, & \text{если } x < 2; \end{cases}$$

Таблица значений:

График обратной функции:

в) Функция:

$$y = \begin{cases} -x, & \text{если } x < 0; \\ -3x, & \text{если } x \geq 0. \end{cases}$$

Для $x < 0$:

При $x < 0$, $y = -x$. Рассмотрим неравенства для $y$:

$$y > 0 \quad \Rightarrow \quad x = -y \quad \Rightarrow \quad y = -x.$$

Для $x \geq 0$:

При $x \geq 0$, $y = -3x$. Рассмотрим неравенства для $y$:

$$y \leq 0 \quad \Rightarrow \quad x = -\frac{y}{3} \quad \Rightarrow \quad y = -\frac{1}{3}x.$$

Обратная функция:

Теперь, учитывая вышеизложенное, можем записать обратную функцию:

$$y = \begin{cases} -\frac{1}{3}x, & \text{если } x \leq 0; \\ -x, & \text{если } x > 0. \end{cases}$$

Таблица значений:

График обратной функции:

г) Функция:

$$y = \begin{cases} 2x + 1, & \text{если } x \leq 2; \\ \frac{1}{2}x + 4, & \text{если } x \geq 2. \end{cases}$$

Для $x \leq 2$:

Мы имеем, что $y = 2x + 1$. Рассмотрим выражение для $x$:

$$x = \frac{y — 1}{2}.$$

Для значений $x \leq 2$ функция $y = 2x + 1$ ограничена сверху $y \leq 5$, потому что при $x = 2$ максимальное значение $y$ равно 5.

Для $x \geq 2$:

Мы имеем, что $y = \frac{1}{2}x + 4$. Рассмотрим выражение для $x$:

$$x = 2y — 8.$$

Для значений $x \geq 2$ функция $y = \frac{1}{2}x + 4$ ограничена снизу $y \geq 5$, потому что при $x = 2$ минимальное значение $y$ равно 5.

Обратная функция:

Исходя из вышеуказанных вычислений, обратная функция будет иметь вид:

$$y = \begin{cases} 0.5(x — 1), & \text{если } x \leq 5; \\ 2x — 8, & \text{если } x \geq 5. \end{cases}$$

• Для $x \leq 5$, обратная функция: $y = 0.5(x — 1)$.
• Для $x \geq 5$, обратная функция: $y = 2x — 8$.

Таблица значений:

Рассмотрим таблицу значений для функции и её обратной функции:

• При $x = 1$, $y = 2(1) + 1 = 3$.
• При $x = 5$, $y = 2(5) + 1 = 11$.
• При $x = 6$, $y = \frac{1}{2}(6) + 4 = 7$.

График обратной функции: