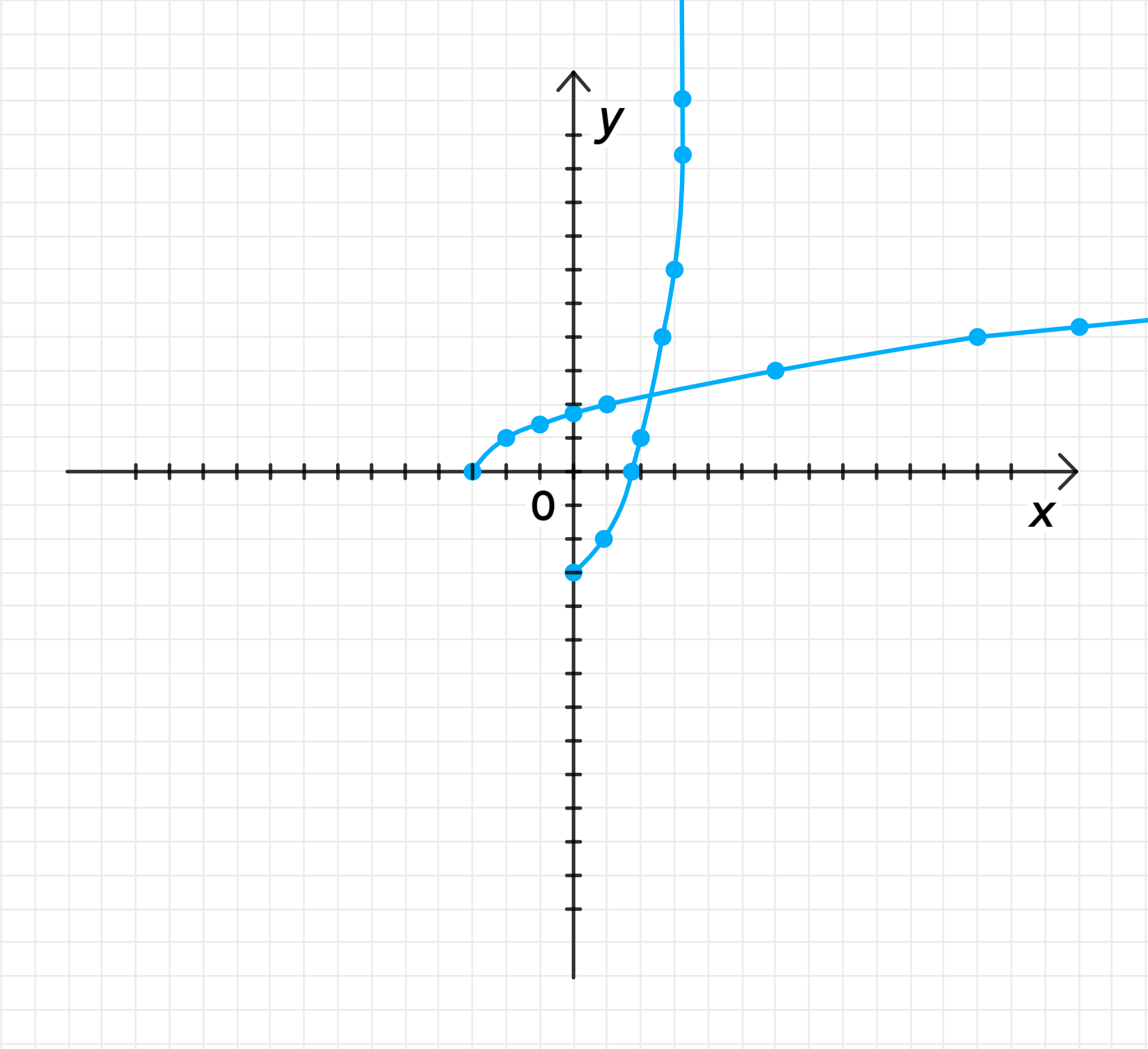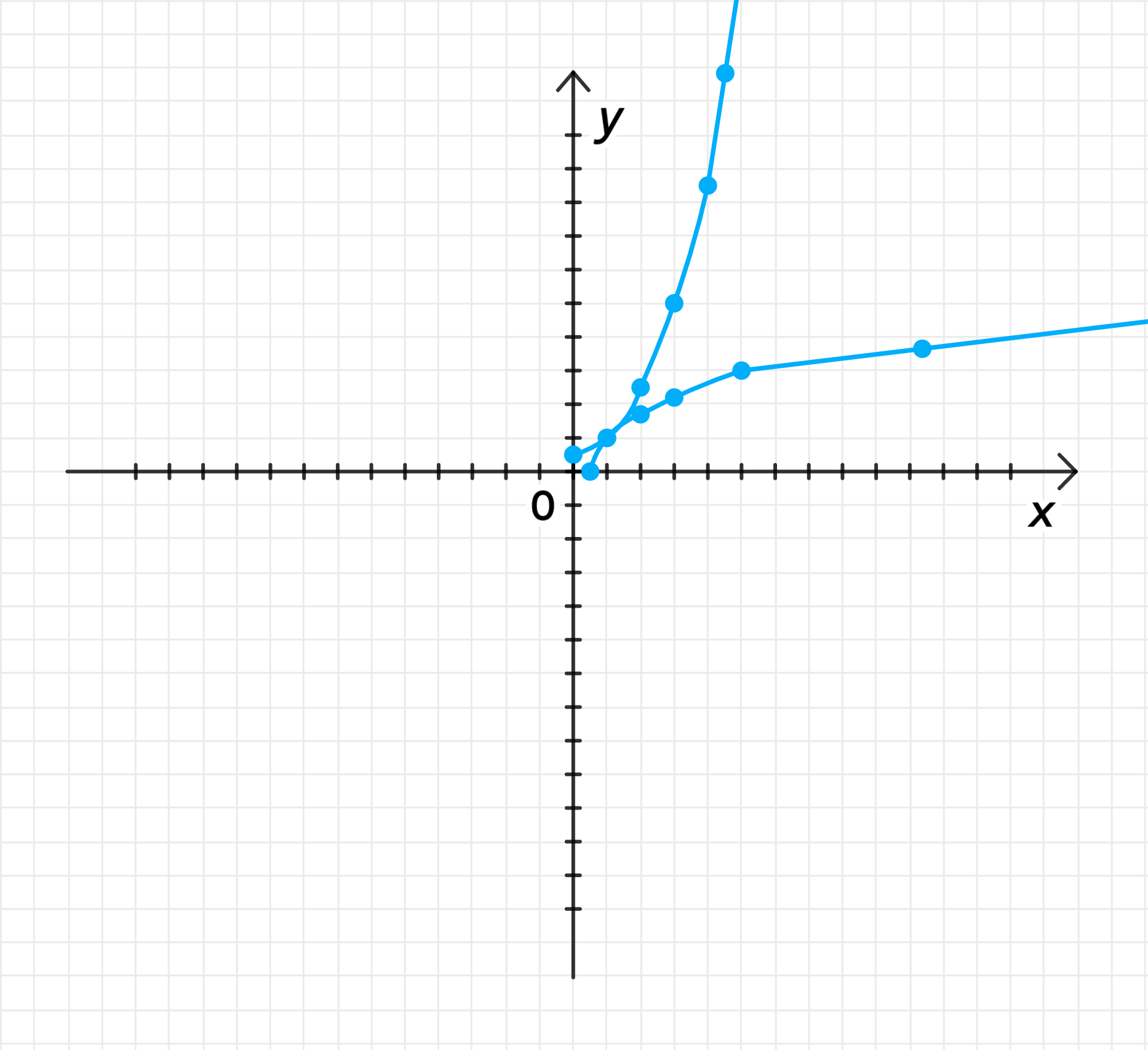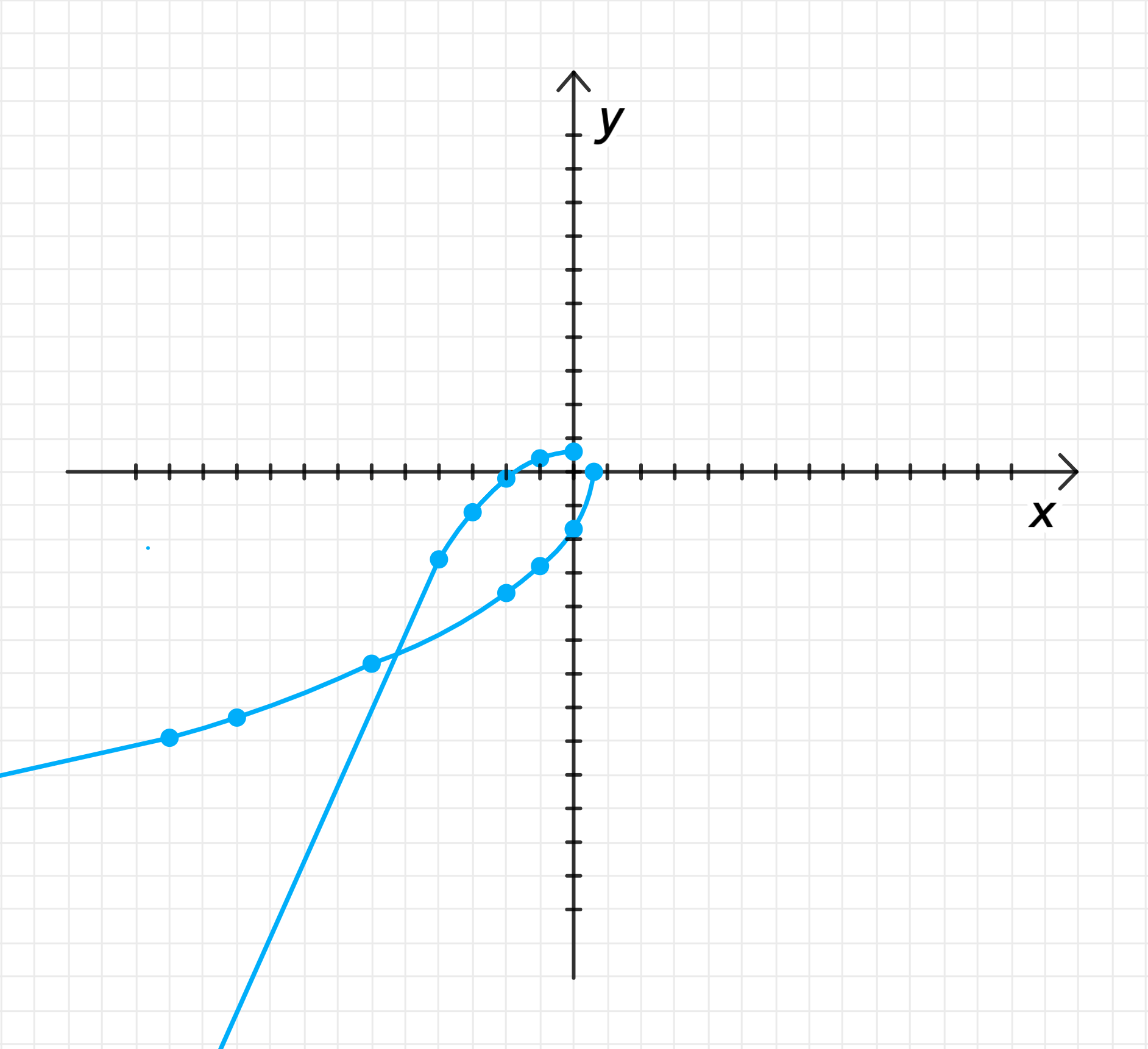Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 10.13 Профильный Уровень Мордкович — Подробные Ответы
Задайте функцию, обратную данной; постройте графики заданной и обратной функций:
а)
б)
в)
г)
а)
Данная функция:
- и ;
- — функция возрастает;
Функция, обратная данной:
- ;
- ;
- , где ;
- и ;
Графики функций:
Ответ: , где .
б)
Данная функция:
- и ;
- — функция возрастает;
Функция, обратная данной:
- ;
- ;
- , где ;
- и ;
Графики функций:
Ответ: , где .
в)
Данная функция:
- и ;
- — функция возрастает;
Функция, обратная данной:
- ;
- ;
- ;
- , где ;
- и ;
Графики функций:
Ответ: , где .
г)
Данная функция:
- и ;
- — функция возрастает;
Функция, обратная данной:
- ;
- ;
- ;
- , где ;
- и ;
Графики функций:
Ответ: , где .
а)
Анализ данной функции:
- Функция задана как .
- Предел области определения функции: для выражения , чтобы значение под корнем было неотрицательным, требуется , то есть . Таким образом, область определения функции: .
- Точка пересечения с осью (когда ): . Точка , .
- Производная функции:
Для производная всегда положительная, так как знаменатель всегда положителен (корень из положительного числа). Это означает, что функция возрастает на всей области определения.
- и — функция возрастает.
Таблица значений функции для нескольких значений :
- При , .
- При , .
- При , .
- При , .
Обратная функция:
Мы ищем функцию, обратную данной, то есть такую, которая выражает через . Для этого:
Возводим обе стороны в квадрат:
Таким образом, обратная функция: , где (так как , и значение под корнем всегда неотрицательное).
Точка пересечения с осью (когда ): . Точка , .
Таблица значений для обратной функции:
- При , .
- При , .
- При , .
- При , .
Графики функций:
Ответ: , где .
б)
Анализ данной функции:
- Функция задана как .
- Предел области определения функции: для выражения , чтобы значение под корнем было неотрицательным, требуется , то есть . Таким образом, область определения функции: .
- Точка пересечения с осью (когда ): . Точка , .
- Производная функции:
Для производная всегда отрицательная, так как знаменатель всегда положительный (корень из положительного числа), а знак минус перед производной указывает на убывание функции на всей области определения.
- и — функция убывает.
Таблица значений функции для нескольких значений :
Обратная функция:
Мы ищем функцию, обратную данной, то есть такую, которая выражает через . Для этого:
Возводим обе стороны в квадрат:
Таким образом, обратная функция: , где (так как , и функция всегда принимает отрицательные значения).
Точка пересечения с осью (когда ): . Точка , .
Таблица значений для обратной функции:
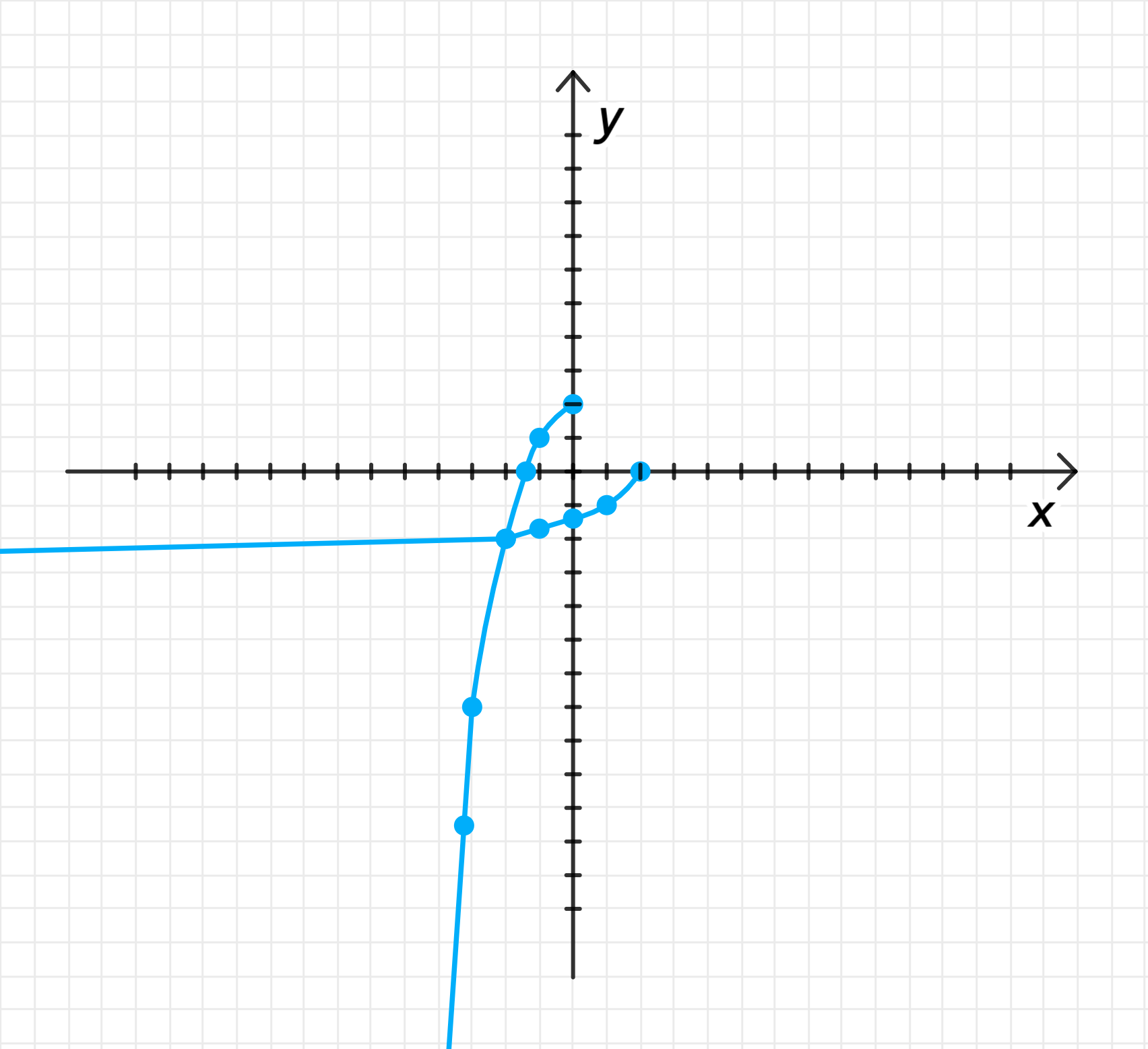
Графики функций:
Ответ: , где .
в)
Анализ данной функции:
- Функция задана как .
- Предел области определения функции: для выражения , чтобы значение под корнем было неотрицательным, требуется , то есть . Таким образом, область определения функции: .
- Точка пересечения с осью (когда ): . Точка , .
- Производная функции:
Для производная всегда положительная, так как знаменатель всегда положителен (корень из положительного числа). Это означает, что функция возрастает на всей области определения.
- и — функция возрастает.
Таблица значений функции для нескольких значений :
Обратная функция:
Мы ищем функцию, обратную данной, то есть такую, которая выражает через . Для этого:
Возводим обе стороны в квадрат:
Таким образом, обратная функция: , где .
Точка пересечения с осью (когда ): . Точка , .
Таблица значений для обратной функции:
Графики функций:
Ответ: , где .
г)
Анализ данной функции:
- Функция задана как .
- Предел области определения функции: для выражения , чтобы значение под корнем было неотрицательным, требуется , то есть . Таким образом, область определения функции: .
- Точка пересечения с осью (когда ): . Точка , .
- Производная функции:
Для производная всегда отрицательная, так как знаменатель всегда положительный (корень из положительного числа), а знак минус перед производной указывает на убывание функции на всей области определения.
- и — функция убывает.
Таблица значений функции для нескольких значений :
Обратная функция:
Мы ищем функцию, обратную данной, то есть такую, которая выражает через . Для этого:
Возводим обе стороны в квадрат:
Таким образом, обратная функция: , где .
Точка пересечения с осью (когда ): . Точка , .
Таблица значений для обратной функции:
Графики функций:
Ответ: , где .