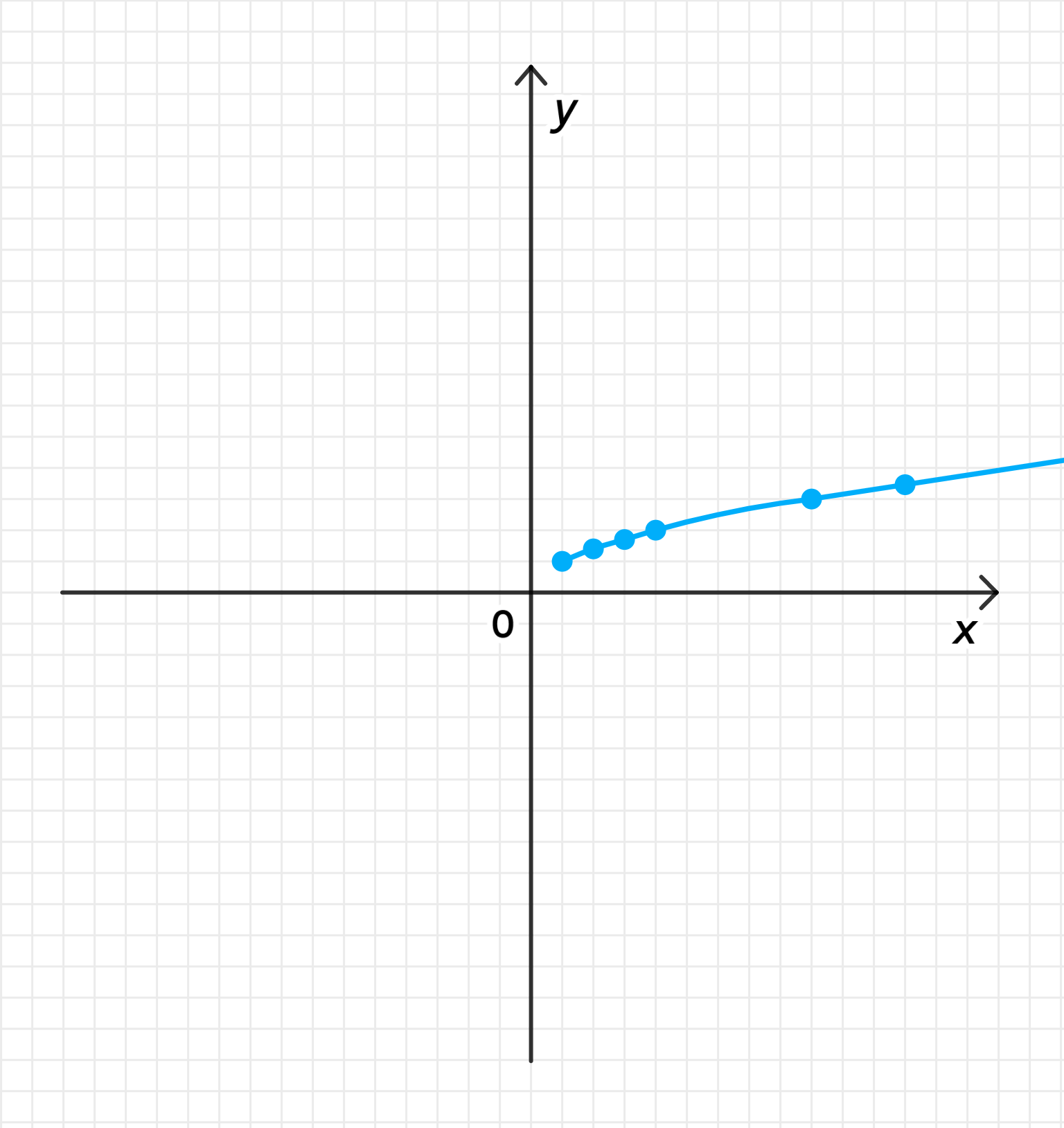Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 10.19 Профильный Уровень Мордкович — Подробные Ответы
Рассмотрите данную функцию на каждом из указанных промежутков; если она на этом промежутке имеет обратную функцию, то задайте обратную функцию аналитически, укажите ее область определения и область значений, постройте ее график:
у = x²:
а) на R;
б) на [1;
в) на (-1; 5];
г) на (; 0].
У квадратичной функции обратная функция может существовать только на промежутках, содержащих одну ветвь параболы;
Дана функция: ;
;
— ветви направлены вверх;
а) На множестве обратной функции не существует;
Ответ: нет.
б) На промежутке :
Множество значений функции:
Функция, обратная данной:
| 1 | 4 | 9 | |
|---|---|---|---|
| 1 | 2 | 3 |
График обратной функции:
Ответ:
в) На промежутке обратной функции не существует;
Ответ: нет.
г) На промежутке :
Множество значений функции:
Функция, обратная данной:
| 0 | 1 | 4 | 9 | |
|---|---|---|---|---|
| 0 | -1 | -2 | -3 |
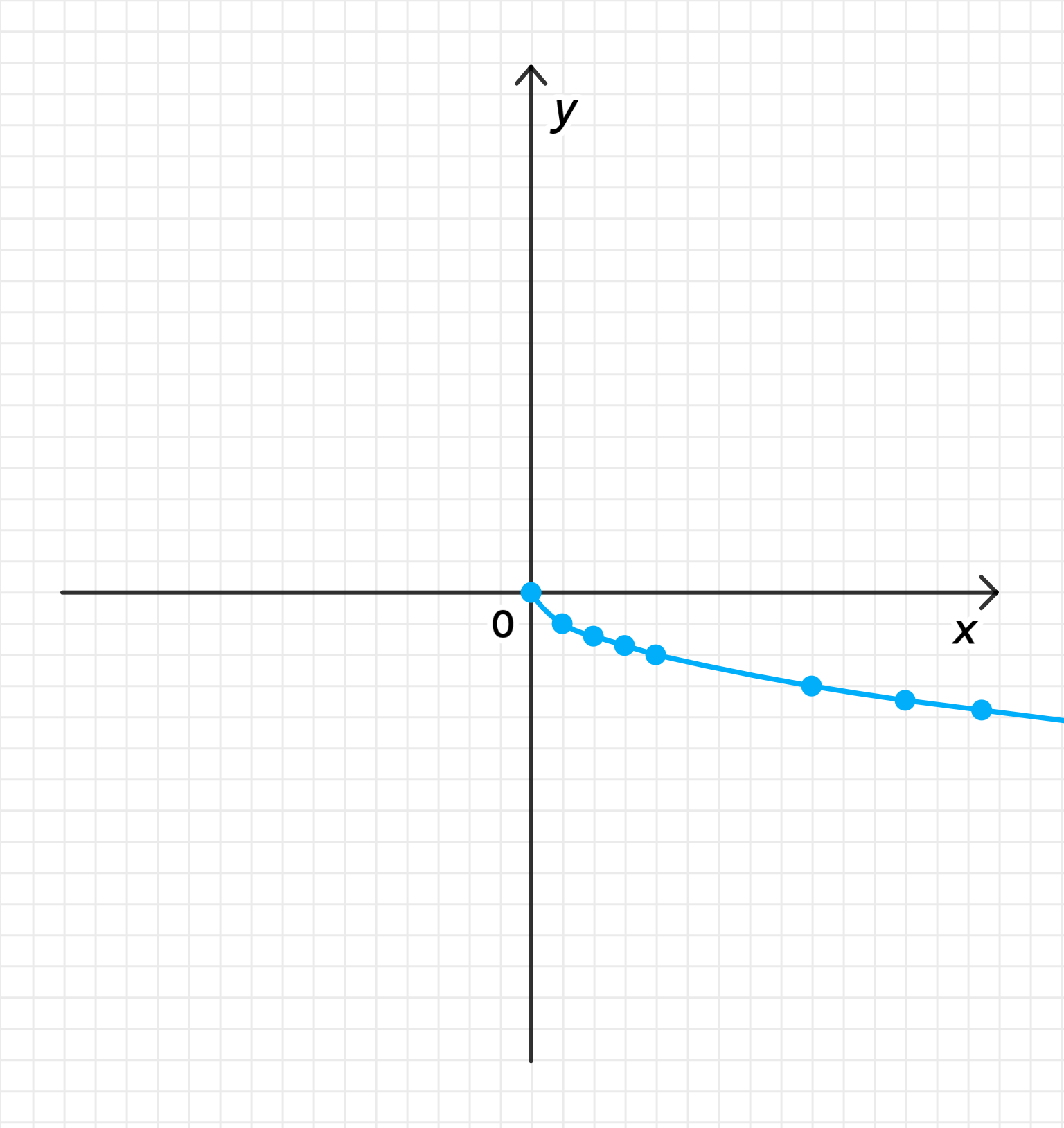
График обратной функции:
Ответ:
Дано:
, где и , (для квадратичной функции).
Мы хотим найти обратную функцию на различных промежутках.
Важные замечания:
Обратная функция существует только на промежутке, содержащем одну ветвь параболы. Это важно, потому что квадратичная функция не является взаимно однозначной на всей области определения: для любого значения существует два значения , одно положительное и одно отрицательное (например, и дают одинаковое значение ).
Обратная функция: Чтобы найти обратную функцию, нужно решить уравнение относительно , но при этом нужно ограничивать область значений , чтобы функция была взаимно однозначной.
1. Анализ функции
Параметры функции:
Квадратичная функция имеет вид , где , , .
Вершина параболы: так как , парабола направлена вверх, а её вершина находится в точке , то есть в точке .
Область значений функции , так как парабола направлена вверх, и на промежутке функция монотонно возрастает.
Область определения: вся область , так как квадратичная функция определена для всех .
2. Рассмотрим каждый из промежутков
а) На множестве обратной функции не существует
Обратная функция существует только на промежутке, где функция является взаимно однозначной. Вся область определения включает обе ветви параболы: одну с положительными значениями (для ) и другую с отрицательными значениями (для ).
На всей области не существует обратной функции, потому что одно и то же значение может быть получено двумя различными значениями . Например, для значения и дают одинаковый результат.
Следовательно, обратная функция не существует на всей области .
Ответ: нет.
б) На промежутке
Этот промежуток содержит только одну ветвь параболы (положительную), и на нём функция является монотонной (возрастающей).
Множество значений функции:
- Минимальное значение функции на этом промежутке: .
- Множество значений функции: , так как на этом промежутке принимает значения от 1 до бесконечности.
Нахождение обратной функции:
Чтобы найти обратную функцию, выразим через :
Обратная функция будет иметь вид:
Это означает, что на промежутке обратная функция существует и выглядит как .
Таблица значений для функции и её обратной:
| 1 | 4 | 9 | |
|---|---|---|---|
| 1 | 2 | 3 |
График обратной функции:
График функции — это парабола, направленная вверх, и она существует только для .
Ответ:
в) На промежутке обратной функции не существует
На данном промежутке функция принимает два различных значения для каждого . Например, для на промежутке значения и обе приводят к тому, что . Таким образом, функция не является взаимно однозначной, и её обратная функция не существует на этом промежутке.
Ответ: нет.
г) На промежутке
Этот промежуток соответствует одной из ветвей параболы, которая направлена вниз.
Множество значений функции:
- Минимальное значение функции на этом промежутке: .
- Множество значений функции: , так как функция на этом промежутке принимает значения от 0 до бесконечности.
Нахождение обратной функции:
Для функции на промежутке нам нужно выразить через . Поскольку мы рассматриваем отрицательную ветвь параболы, то:
Обратная функция будет иметь вид:
Таблица значений для функции и её обратной:
| 0 | 1 | 4 | 9 | |
|---|---|---|---|---|
| 0 | -1 | -2 | -3 |
График обратной функции:
График функции — это парабола, направленная вниз, и она существует только для .
Ответ:
Итоговый ответ:
а) На множестве обратной функции не существует. Ответ: нет.
б) На промежутке обратная функция существует. Ответ: .
в) На промежутке обратной функции не существует. Ответ: нет.
г) На промежутке обратная функция существует. Ответ: .