Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 10.20 Профильный Уровень Мордкович — Подробные Ответы
у = x² — 2:
а) на R;
б) на [1; 2);
в) на (-1; 5];
г) на [-2; 0].
У квадратичной функции обратная функция может существовать только на промежутках, содержащих одну ветвь параболы;
Дана функция: ;
;
— ветви направлены вверх;
а) На множестве обратной функции не существует;
Ответ: нет.
б) На промежутке :
Множество значений функции:
Функция, обратная данной:
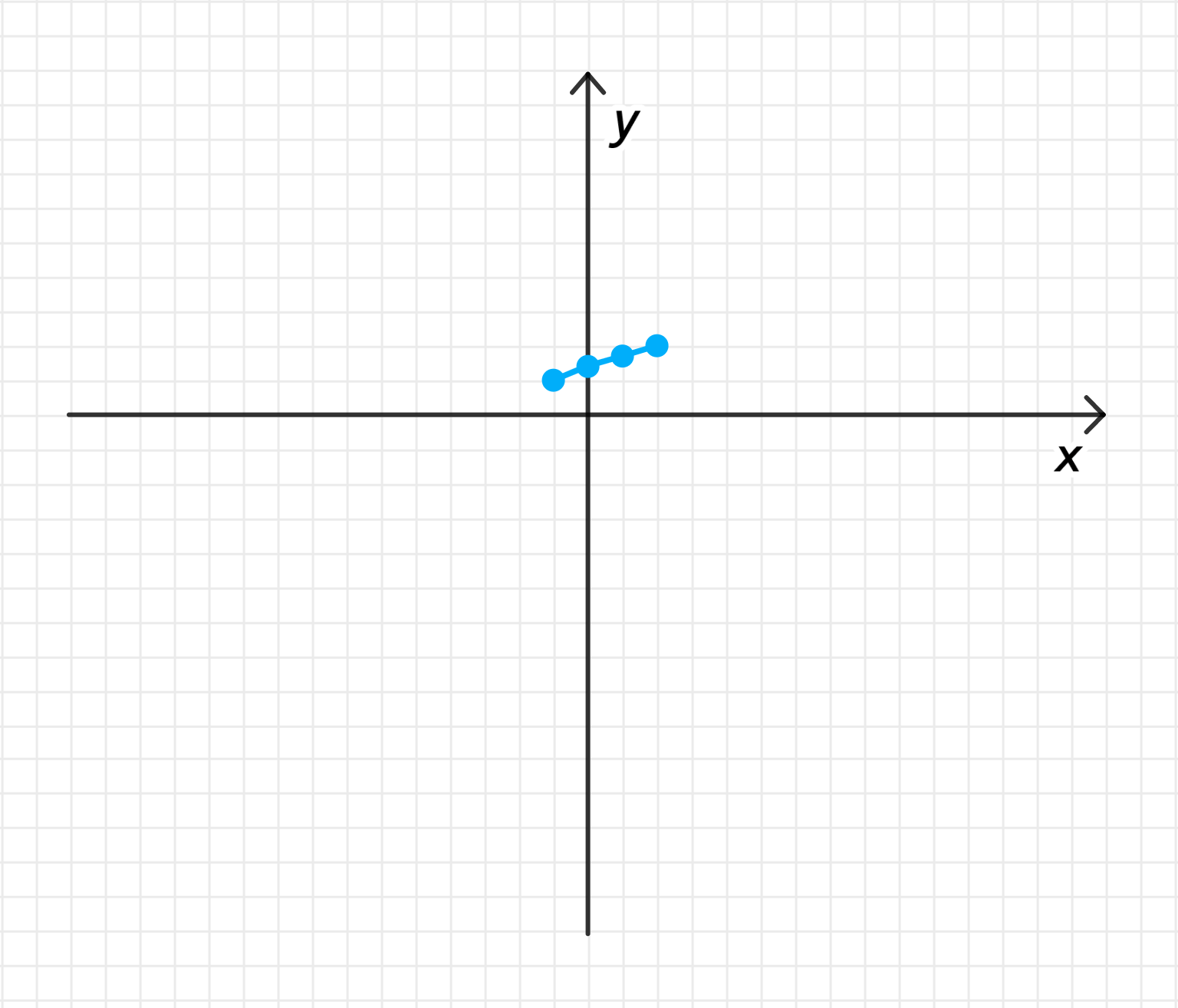
График обратной функции:
Ответ: .
в) На промежутке обратной функции не существует;
Ответ: нет.
г) На промежутке :
Множество значений функции:
Функция, обратная данной:
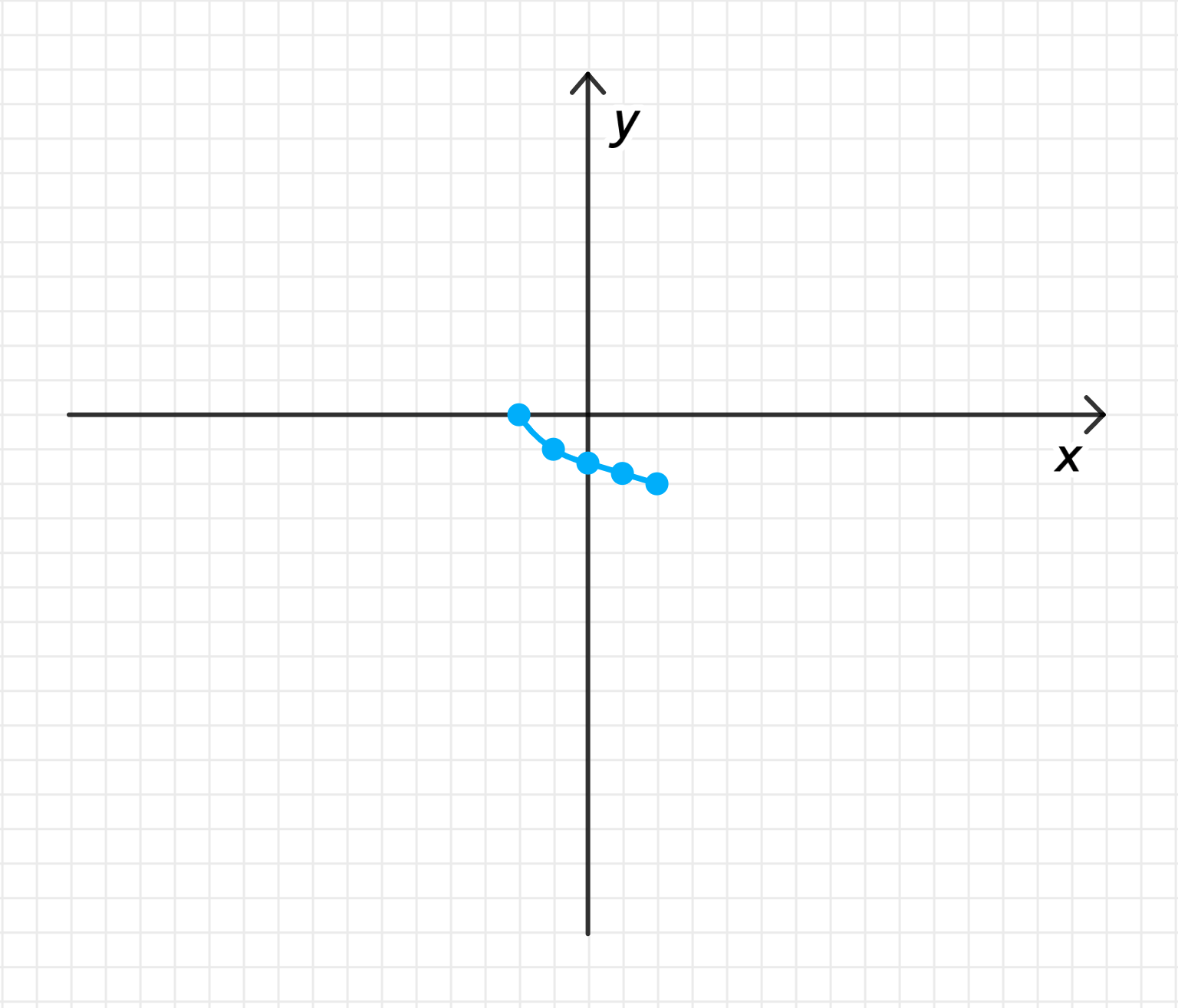
График обратной функции:
Ответ: .
Квадратичная функция:
Параметры функции:
(коэффициент при , положительный — парабола открывается вверх).
(коэффициент при ).
(свободный член).
Вершина параболы:
Для квадратичной функции вида вершина находится в точке:
Подставляя в исходную функцию, получаем значение функции в вершине:
Таким образом, вершина параболы находится в точке .
Направление ветвей:
Так как , то парабола направлена вверх, и её ветви растут, начиная с минимального значения в вершине.
Область определения функции :
Поскольку это квадратичная функция, её область определения — вся действительная прямая , то есть:
Область значений функции :
Функция достигает минимального значения в вершине, и это минимальное значение равно . Поскольку парабола открывается вверх, значения функции на промежутке будут возрастающими, а на промежутке — также возрастающими, но для отрицательных .
Таким образом, область значений функции:
1. Обратная функция для квадратичной функции
Для нахождения обратной функции нам нужно решить уравнение относительно . Однако так как квадратичная функция не является взаимно однозначной на всей области определения, нужно рассматривать обратные функции на отдельных промежутках.
2. Разбор задачи по промежуткам
а) На множестве обратной функции не существует
На всей области функция не является взаимно однозначной. Это связано с тем, что для любого положительного значения существует два значения , одно положительное и одно отрицательное (например, для значения и дают одинаковое значение ).
Ответ: нет, на множестве обратной функции не существует.
б) На промежутке
На данном промежутке функция является монотонной (возрастающей). Мы можем найти обратную функцию для этого промежутка.
Множество значений функции:
Для промежутка находим значения функции:
Минимальное значение функции при :
Максимальное значение функции при :
Таким образом, множество значений функции на промежутке будет:
Нахождение обратной функции:
Для нахождения обратной функции, выразим через :
Так как на промежутке всегда положительное, то обратная функция будет:
Таким образом, обратная функция для промежутка имеет вид:
Таблица значений для функции и её обратной:
График обратной функции:
Ответ:
.
в) На промежутке обратной функции не существует
На промежутке функция не является взаимно однозначной, так как на промежутке от до значения могут быть одинаковыми для разных . Например, для на промежутке значения и дают одинаковое значение .
Ответ: нет, на промежутке обратной функции не существует.
г) На промежутке
На данном промежутке функция монотонно убывает, и она является взаимно однозначной на этом промежутке. Мы можем найти её обратную функцию для этого промежутка.
Множество значений функции:
Для промежутка находим значения функции:
Минимальное значение функции при :
Максимальное значение функции при :
Таким образом, множество значений функции на промежутке будет:
Нахождение обратной функции:
Для нахождения обратной функции, выразим через :
Так как на промежутке всегда отрицательное, то обратная функция будет:
Таким образом, обратная функция для промежутка имеет вид:
Таблица значений для функции и её обратной:
График обратной функции:
Ответ:
.
Итоговый ответ:
а) На множестве обратной функции не существует. Ответ: нет.
б) На промежутке обратная функция существует. Ответ: .
в) На промежутке обратной функции не существует. Ответ: нет.
г) На промежутке обратная функция существует. Ответ: .