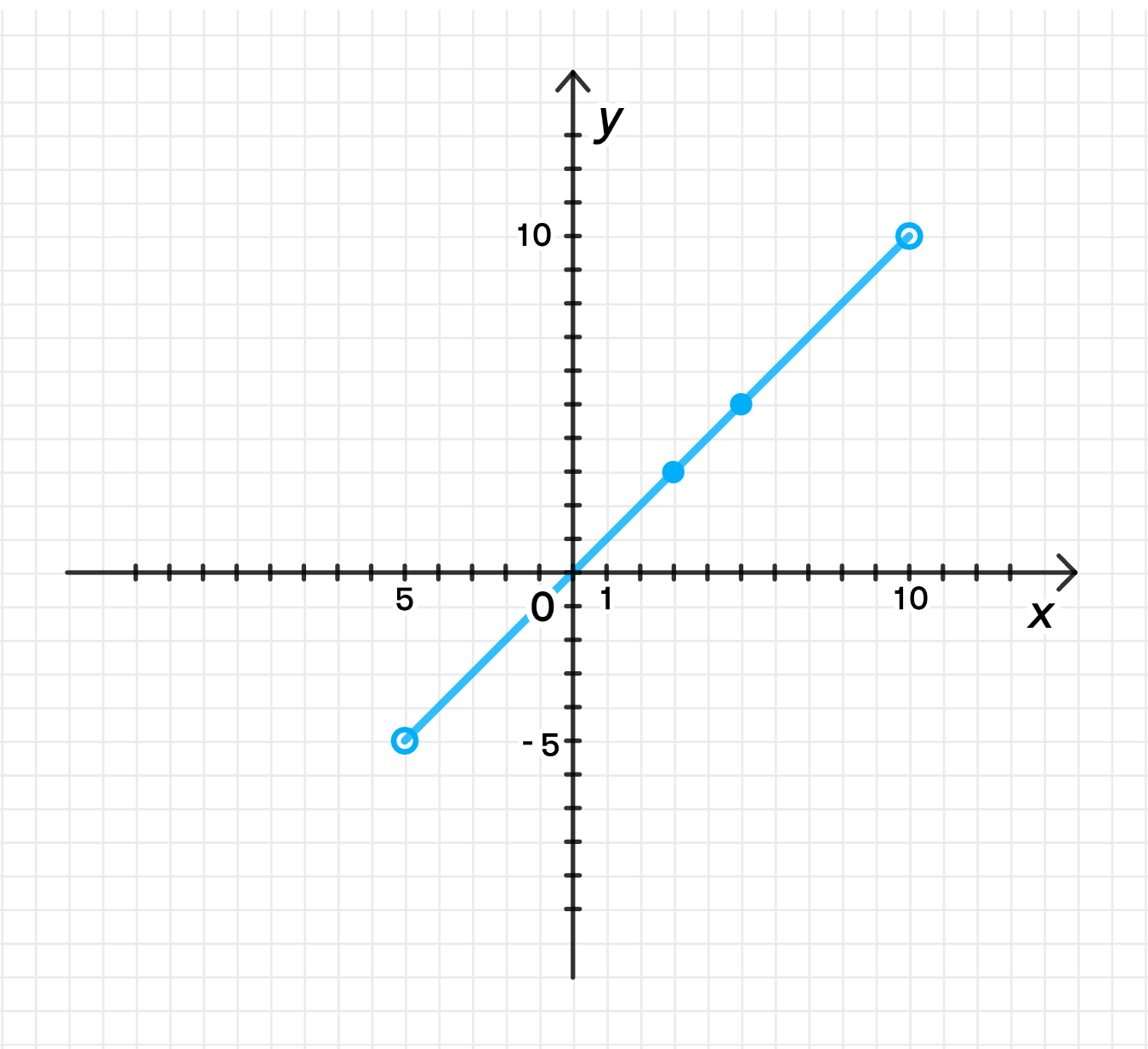Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 10.24 Профильный Уровень Мордкович — Подробные Ответы
Постройте на одном чертеже какие-нибудь графики двух взаимно-обратных непрерывных на (-5; 10) функций у = f(x) и у = g(x), для которых:
а) f(3) = 3, g(5) = 5;
б) f(3) = 7, f(7) = 8, g(9) = 9;
в) f(1) = -1, g(3) = 3;
г) f(1) = 9, f(2) = 7, g(4) = 4.
Построить графики двух взаимно обратных функций, непрерывных, на промежутке , и , для которых:
а) и ;
Так как функции взаимно обратны:
Графики функций:
б) , и ;
Так как функции взаимно обратны:
Графики функций:
в) и ;
Так как функции взаимно обратны:
Графики функций:
г) , и ;
Так как функции взаимно обратны:
Графики функций:
а) и .
Взаимность функций:
Если и взаимно обратны, это означает, что для всех выполняется равенство:
Таким образом, если , то должно быть равно , потому что — это обратная функция для и наоборот.
В данном случае:
Графики функций:
- График функции будет проходить через точку , так как , и через точку , так как .
- График функции будет проходить через точку , так как , и через точку , так как .
Если и действительно взаимно обратны, их графики будут симметричны относительно прямой , так как если точка лежит на графике , то точка будет лежать на графике .
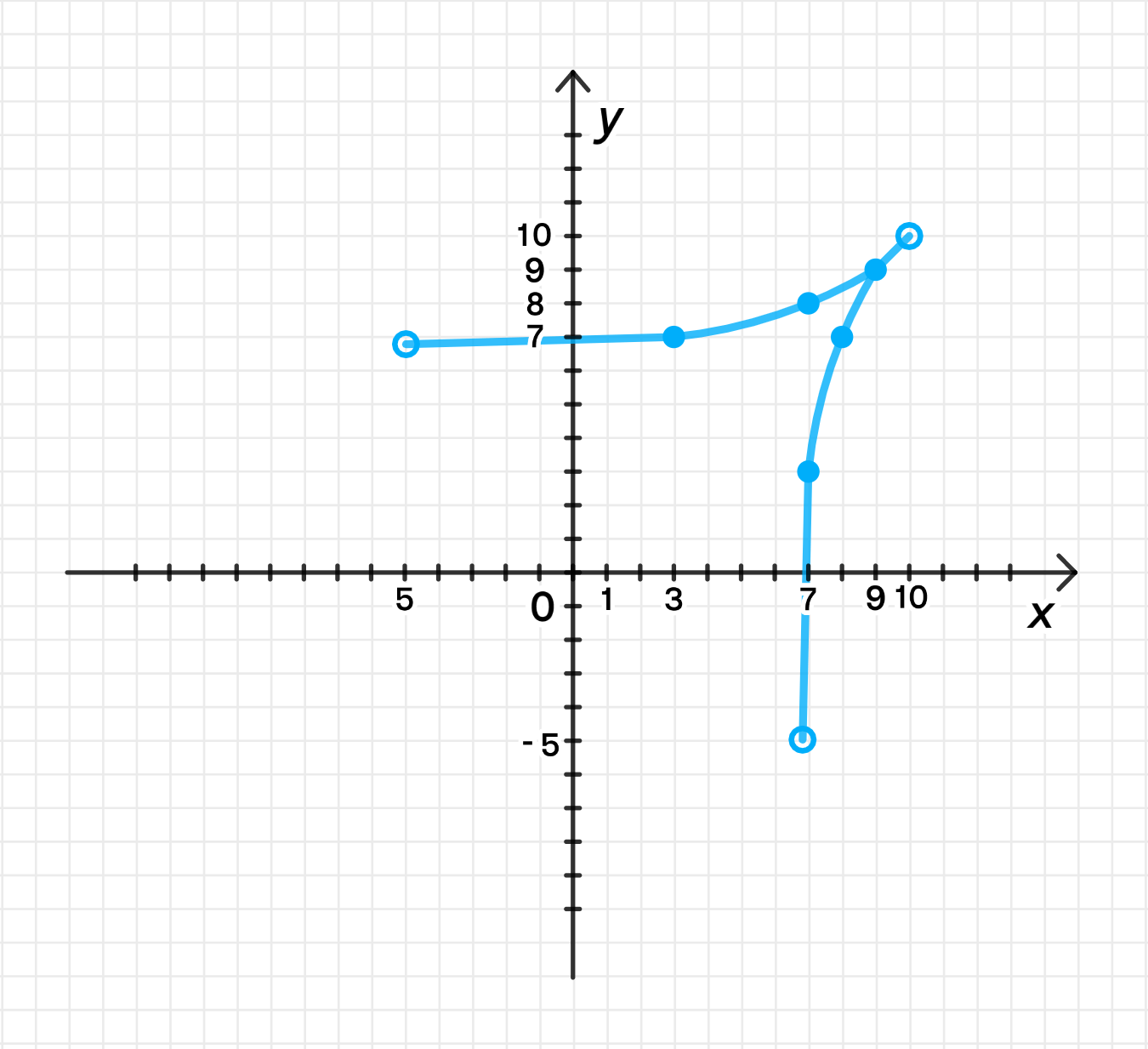
б) , и .
Взаимность функций:
Поскольку функции взаимно обратны, то для каждого значения выполняются следующие равенства:
- , то есть , так как — это обратная функция для .
- , то есть , так как — это обратная функция для .
- , то есть , так как — это обратная функция для .
Графики функций:
- График функции будет проходить через точки , , и , так как , , и .
- График функции будет проходить через точки , , и , так как , , и .
Эти графики также будут симметричны относительно прямой .
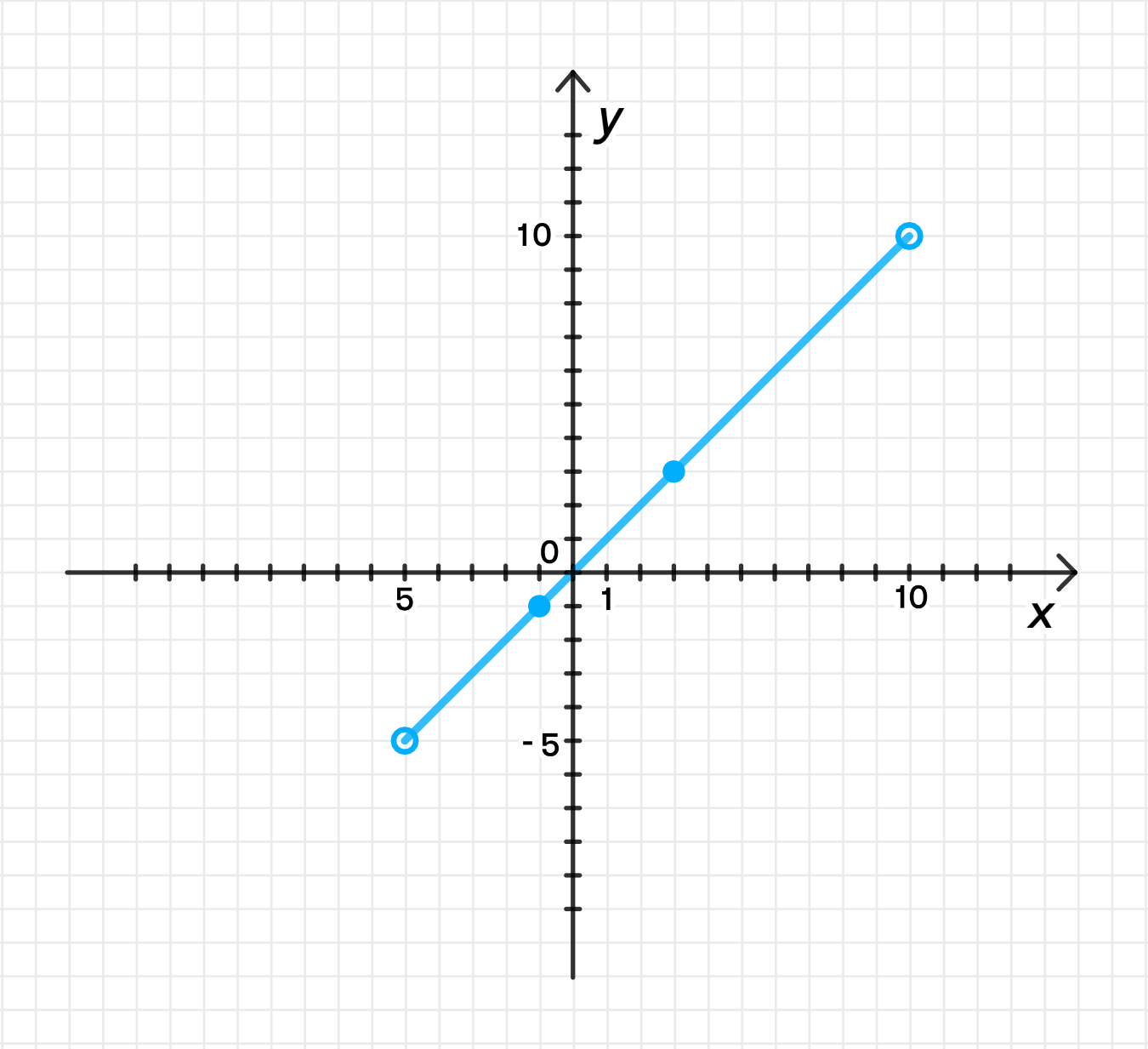
в) и .
Взаимность функций:
Взаимность функций означает, что для каждой точки выполняются равенства:
- , то есть , так как — это обратная функция для .
- , то есть , так как — это обратная функция для .
Графики функций:
- График функции будет проходить через точку , так как .
- График функции будет проходить через точку , так как .
Обе функции будут симметричны относительно прямой , так как они взаимно обратны.
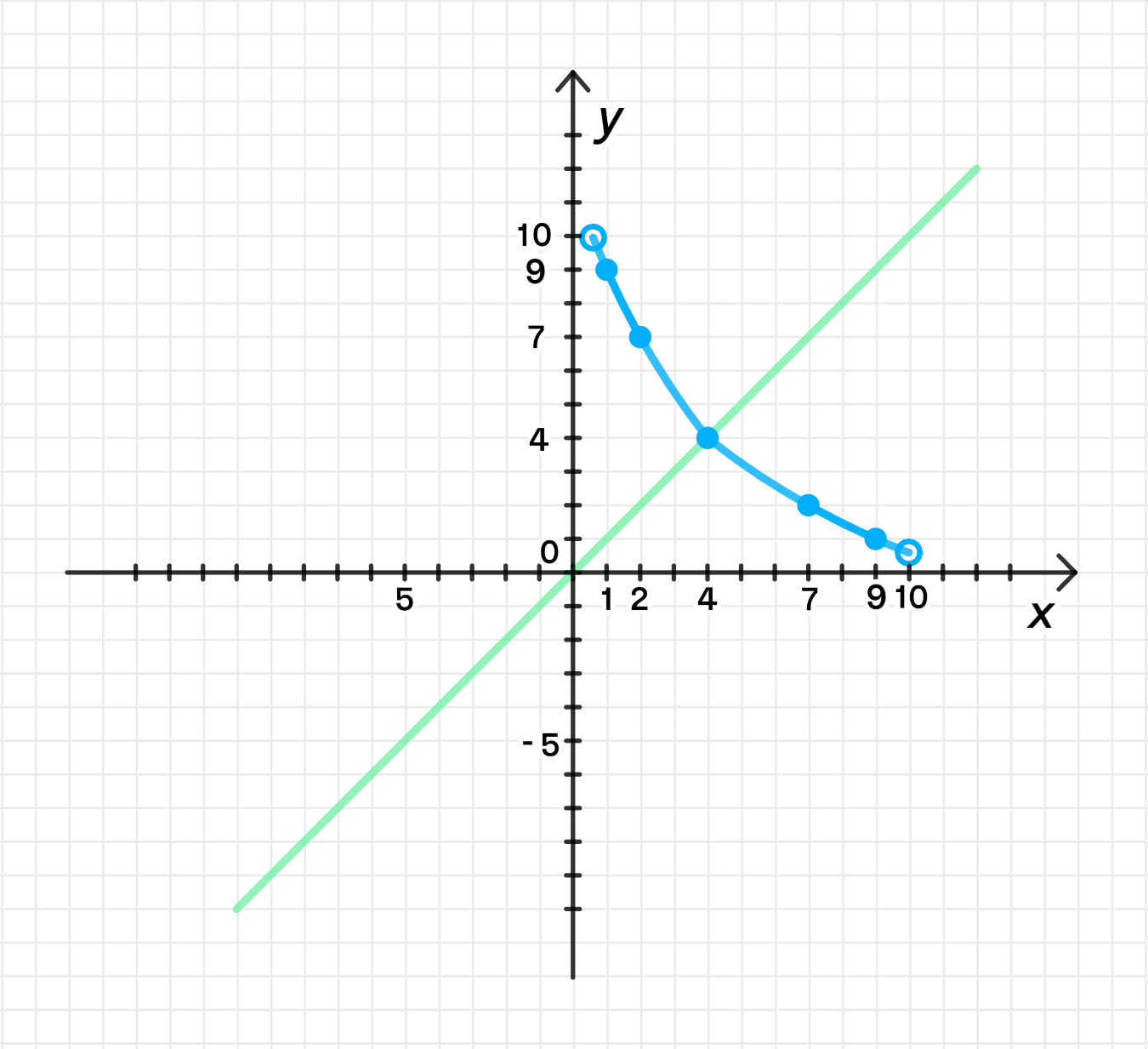
г) , и .
Взаимность функций:
Поскольку функции взаимно обратны, для каждого значения выполняются равенства:
- , то есть , так как — это обратная функция для .
- , то есть , так как — это обратная функция для .
- , то есть , так как — это обратная функция для .
Графики функций:
- График функции будет проходить через точки , , и , так как , , и .
- График функции будет проходить через точки , , и , так как , , и .
Эти графики также будут симметричны относительно прямой .