ГДЗ по Алгебре 10 Класс Номер 10.26 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции у = f(g(x)), если:

а) f(x) = 4x, g(x) = 0,25x;

б) f(x) = x — 3, g(x) = x + 3;

в) f(x) = -2x, g(x) = -0,5x;

г) f(x) = -5x + 5, g(х) = -0,2x — 1.

Построить график функции $y = f(g(x))$;

а) $f(x) = 4x$ и $g(x) = 0,25x$;

Искомая функция:

$$y = f(g(x)) = f(0,25x) = 4 \cdot 0,25x = x;$$

График функции:

б) $f(x) = x — 3$ и $g(x) = x + 3$;

Искомая функция:

$$y = f(g(x)) = f(x + 3) = (x + 3) — 3 = x;$$

График функции:

в) $f(x) = -2x$ и $g(x) = -0,5x$;

Искомая функция:

$$y = f(g(x)) = f(-0,5x) = -2 \cdot (-0,5x) = x;$$

График функции:

г) $f(x) = -5x + 5$ и $g(x) = -0,2x — 1$;

Искомая функция:

$$y = f(g(x)) = f(-0,2x — 1);$$ $$y = -5(-0,2x — 1) + 5 = x — 5 + 5 = x;$$

График функции:

Построить график функции $y = f(g(x))$.

а) $f(x) = 4x$ и $g(x) = 0,25x$

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = 4x$
• $g(x) = 0,25x$

Нам нужно найти композицию $f(g(x))$, то есть $f$ от $g(x)$:

$$f(g(x)) = f(0,25x).$$

Подставляем $0,25x$ в выражение для $f(x)$:

$$f(0,25x) = 4 \cdot 0,25x = x.$$

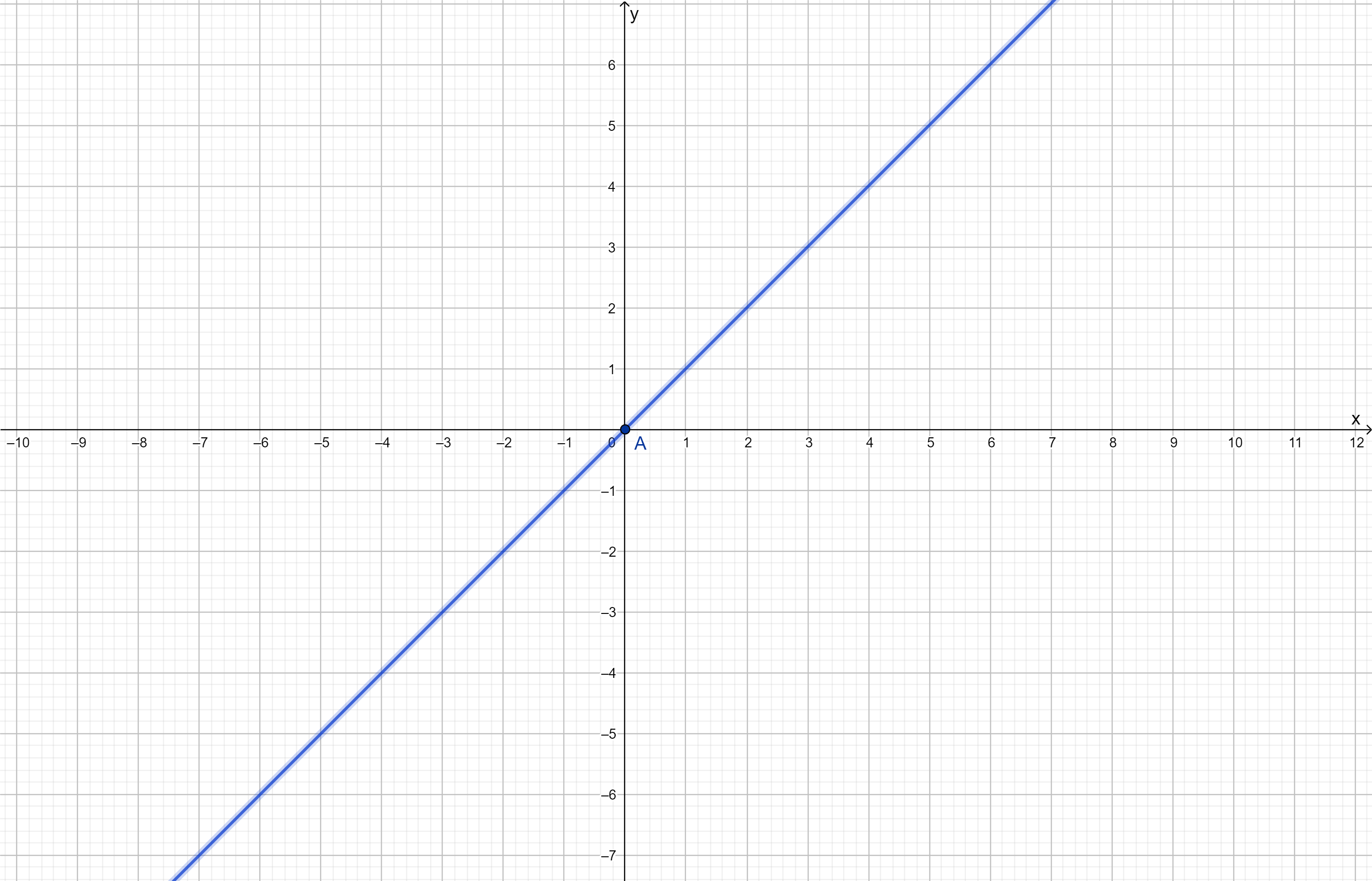
Таким образом, композиция двух функций дает просто $x$. Это означает, что график функции $f(g(x))$ будет совпадать с графиком функции $y = x$, то есть с прямой, которая проходит через начало координат с угловым коэффициентом 1.

Шаг 2: График функции:

Поскольку результат композиции равен $x$, график этой функции — это прямая линия с угловым коэффициентом 1, которая проходит через начало координат. Эта прямая — стандартная диагональ в системе координат.

б) $f(x) = x — 3$ и $g(x) = x + 3$

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = x — 3$
• $g(x) = x + 3$

Нам нужно найти композицию $f(g(x))$:

$$f(g(x)) = f(x + 3).$$

Подставляем $x + 3$ в выражение для $f(x)$:

$$f(x + 3) = (x + 3) — 3 = x.$$

Таким образом, композиция двух функций также дает $x$. Это значит, что результат будет тот же — график функции $f(g(x))$ будет совпадать с графиком функции $y = x$.

Шаг 2: График функции:

Как и в предыдущем случае, график этой функции — это прямая линия с угловым коэффициентом 1, которая проходит через начало координат.

в) $f(x) = -2x$ и $g(x) = -0,5x$

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = -2x$
• $g(x) = -0,5x$

Нам нужно найти композицию $f(g(x))$:

$$f(g(x)) = f(-0,5x).$$

Подставляем $-0,5x$ в выражение для $f(x)$:

$$f(-0,5x) = -2 \cdot (-0,5x) = x.$$

Таким образом, композиция $f(g(x))$ снова дает $x$. Это означает, что график функции будет точно такой же, как и в предыдущих случаях, то есть прямая $y = x$.

Шаг 2: График функции:

Так как результат композиций опять-таки $x$, график этой функции — это прямая линия с угловым коэффициентом 1, которая проходит через начало координат.

г) $f(x) = -5x + 5$ и $g(x) = -0,2x — 1$

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = -5x + 5$
• $g(x) = -0,2x — 1$

Нам нужно найти композицию $f(g(x))$:

$$f(g(x)) = f(-0,2x — 1).$$

Подставляем $-0,2x — 1$ в выражение для $f(x)$:

$$f(-0,2x — 1) = -5(-0,2x — 1) + 5.$$

Раскрываем скобки:

$$= 1x + 5 + 5 = x.$$

Таким образом, композиция функций также дает $x$. Как и в предыдущих случаях, график функции $f(g(x))$ будет совпадать с графиком функции $y = x$.

Шаг 2: График функции:

Поскольку результат композиции — это просто $x$, график функции будет прямой линией, которая проходит через начало координат с угловым коэффициентом 1.