ГДЗ по Алгебре 10 Класс Номер 10.27 Профильный Уровень Мордкович — Подробные Ответы

а) $f(x) = \frac{3}{x}$ и $g(x) = \frac{3}{x}$;

б) $f(x) = \frac{3}{x+1}$ и $g(x) = \frac{3-x}{x}$;

в) $f(x) = \frac{1}{2x}$ и $g(x) = \frac{1}{2x}$;

г) $f(x) = \frac{x-1}{x+1}$ и $g(x) = \frac{x+1}{1-x}$

Построить график функции $y = f(g(x))$;

а) $f(x) = \frac{3}{x}$ и $g(x) = \frac{3}{x}$;

Искомая функция:

$$y = f(g(x)) = f\left(\frac{3}{x}\right) = 3 : \frac{3}{x} = 3 \cdot \frac{x}{3} = x;$$

Выражение имеет смысл при:

$$x \neq 0;$$ $$\frac{3}{x} \neq 0 \quad \Rightarrow \quad 0x \neq 3 \quad — \text{при любом } x;$$

График функции:

б) $f(x) = \frac{3}{x+1}$ и $g(x) = \frac{3-x}{x}$;

Искомая функция:

$$y = f(g(x)) = f\left(\frac{3-x}{x}\right) = 3 : \left(\frac{3-x}{x} + 1\right);$$ $$y = 3 : \frac{3-x+x}{x} = 3 : \frac{3}{x} = 3 \cdot \frac{x}{3} = x;$$

Выражение имеет смысл при:

$$x \neq 0;$$ $$\frac{3-x}{x} + 1 \neq 0 \quad \Rightarrow \quad \frac{3}{x} \neq 0 \quad \Rightarrow \quad x \neq 0;$$

График функции:

в) $f(x) = \frac{1}{2x}$ и $g(x) = \frac{1}{2x}$;

Искомая функция:

$$y = f(g(x)) = f\left(\frac{1}{2x}\right) = \frac{1}{2} : \frac{1}{2x} = \frac{1}{2} \cdot \frac{2x}{1} = x;$$

Выражение имеет смысл при:

$$2x \neq 0 \quad \Rightarrow \quad x \neq 0;$$ $$\frac{2}{2x} \neq 0 \quad \Rightarrow \quad 0x \neq 2 \quad — \text{при любом } x;$$

График функции:

г) $f(x) = \frac{x-1}{x+1}$ и $g(x) = \frac{x+1}{1-x}$;

Искомая функция:

$$y = f(g(x)) = f\left(\frac{x+1}{1-x}\right) = \left(\frac{x+1}{1-x} — 1\right) : \left(\frac{x+1}{1-x} + 1\right);$$ $$y = \frac{x+1-1+x}{1-x} : \frac{x+1+1-x}{1-x} = \frac{2x}{1-x} \cdot \frac{1-x}{2} = x;$$

Выражение имеет смысл при:

$$1 — x \neq 0 \quad \Rightarrow \quad x \neq 1;$$ $$\frac{x+1}{1-x} + 1 \neq 0 \quad \Rightarrow \quad \frac{2}{1-x} \neq 0 \quad \Rightarrow \quad x \neq 1;$$

График функции:

Построить график функции $y = f(g(x))$;

а) $f(x) = \frac{3}{x}$ и $g(x) = \frac{3}{x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = \frac{3}{x}$
• $g(x) = \frac{3}{x}$

Нам нужно найти композицию $f(g(x))$, то есть вычислить $f$ от $g(x)$:

$$f(g(x)) = f\left( \frac{3}{x} \right).$$

Подставляем выражение для $g(x)$ в функцию $f$:

$$f\left( \frac{3}{x} \right) = \frac{3}{\frac{3}{x}} = 3 \cdot \frac{x}{3} = x.$$

Таким образом, композиция $f(g(x))$ дает просто $x$. Это означает, что функция $y = f(g(x))$ является линейной функцией $y = x$.

Шаг 2: Условия, при которых выражение имеет смысл:

Выражение для $f(g(x)) = x$ имеет смысл при том, что функции $f$ и $g$ сами по себе определены.

Функция $g(x) = \frac{3}{x}$ будет определена при $x \neq 0$, так как деление на ноль невозможно.

Следовательно, функция $f(g(x)) = x$ тоже будет определена при $x \neq 0$.

Шаг 3: График функции:

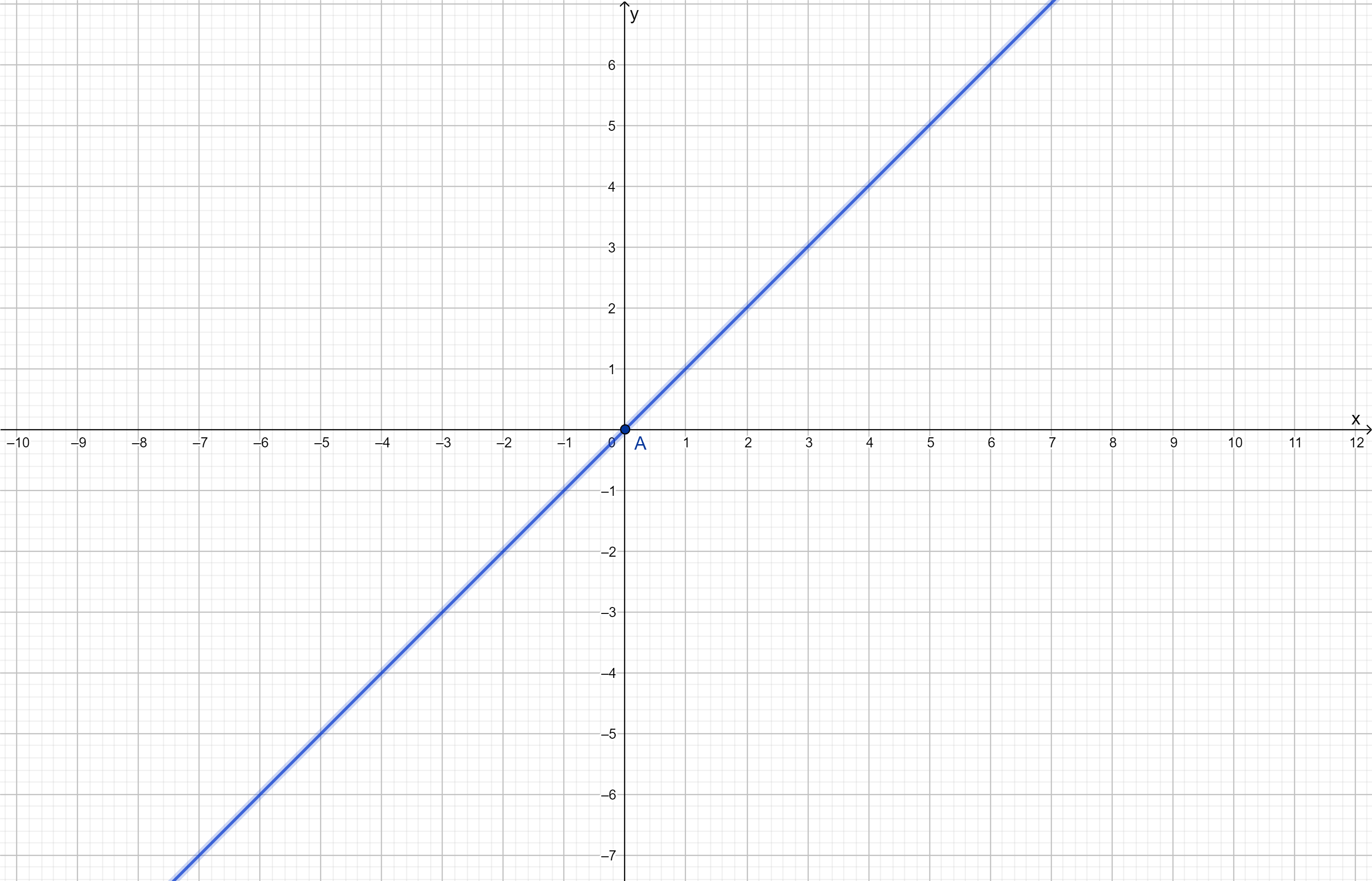
Поскольку результат композиции равен $x$, график функции будет линейной прямой, проходящей через начало координат с угловым коэффициентом 1 (график функции $y = x$).

б) $f(x) = \frac{3}{x+1}$ и $g(x) = \frac{3-x}{x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = \frac{3}{x+1}$
• $g(x) = \frac{3-x}{x}$

Нам нужно найти композицию $f(g(x))$, то есть вычислить $f$ от $g(x)$:

$$f(g(x)) = f\left( \frac{3-x}{x} \right).$$

Подставляем выражение для $g(x)$ в функцию $f$:

$$f\left( \frac{3-x}{x} \right) = \frac{3}{\frac{3-x}{x} + 1}.$$

Преобразуем знаменатель:

$$\frac{3-x}{x} + 1 = \frac{3-x+x}{x} = \frac{3}{x}.$$

Следовательно:

$$f\left( \frac{3-x}{x} \right) = \frac{3}{\frac{3}{x}} = 3 \cdot \frac{x}{3} = x.$$

Шаг 2: Условия, при которых выражение имеет смысл:

Мы видим, что выражение имеет смысл, если:

• $x \neq 0$, чтобы избежать деления на ноль в выражении для $g(x) = \frac{3-x}{x}$.

Дополнительно, для того чтобы $f(x) = \frac{3}{x+1}$ имело смысл, $x + 1 \neq 0$, что также требует $x \neq -1$.

Таким образом, выражение имеет смысл при $x \neq 0$ и $x \neq -1$.

Шаг 3: График функции:

Поскольку композиция дает результат $f(g(x)) = x$, график будет такой же, как и в предыдущем случае: прямая линия с угловым коэффициентом 1, проходящая через начало координат, при условии, что $x \neq 0$ и $x \neq -1$.

в) $f(x) = \frac{1}{2x}$ и $g(x) = \frac{1}{2x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = \frac{1}{2x}$
• $g(x) = \frac{1}{2x}$

Нам нужно найти композицию $f(g(x))$, то есть вычислить $f$ от $g(x)$:

$$f(g(x)) = f\left( \frac{1}{2x} \right).$$

Подставляем выражение для $g(x)$ в функцию $f$:

$$f\left( \frac{1}{2x} \right) = \frac{1}{2 \cdot \frac{1}{2x}} = \frac{1}{\frac{x}{1}} = x.$$

Таким образом, композиция $f(g(x))$ дает $x$. Это означает, что функция $y = f(g(x))$ снова является линейной функцией $y = x$.

Шаг 2: Условия, при которых выражение имеет смысл:

Для выражения $f(g(x)) = x$ быть определенным, необходимо:

• $2x \neq 0$, то есть $x \neq 0$.

Следовательно, выражение имеет смысл при $x \neq 0$.

Шаг 3: График функции:

Поскольку результат композиции снова равен $x$, график будет той же самой прямой с угловым коэффициентом 1, которая проходит через начало координат.

г) $f(x) = \frac{x-1}{x+1}$ и $g(x) = \frac{x+1}{1-x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Нам даны функции:

• $f(x) = \frac{x-1}{x+1}$
• $g(x) = \frac{x+1}{1-x}$

Нам нужно найти композицию $f(g(x))$, то есть вычислить $f$ от $g(x)$:

$$f(g(x)) = f\left( \frac{x+1}{1-x} \right).$$

Подставляем выражение для $g(x)$ в функцию $f$:

$$f\left( \frac{x+1}{1-x} \right) = \frac{\frac{x+1}{1-x} — 1}{\frac{x+1}{1-x} + 1}.$$

Преобразуем числитель и знаменатель:

• Числитель:

  $$\frac{x+1}{1-x} — 1 = \frac{x+1 — (1-x)}{1-x} = \frac{2x}{1-x}.$$

• Знаменатель:

  $$\frac{x+1}{1-x} + 1 = \frac{x+1 + (1-x)}{1-x} = \frac{2}{1-x}.$$

Таким образом:

$$f(g(x)) = \frac{\frac{2x}{1-x}}{\frac{2}{1-x}} = \frac{2x}{2} = x.$$

Шаг 2: Условия, при которых выражение имеет смысл:

Для выражения $f(g(x)) = x$ быть определенным, необходимо:

• $1 — x \neq 0$, то есть $x \neq 1$, чтобы избежать деления на ноль.

Таким образом, выражение имеет смысл при $x \neq 1$.

Шаг 3: График функции:

Результат композиции снова равен $x$, и график будет прямой линией с угловым коэффициентом 1, которая проходит через начало координат при $x \neq 1$.