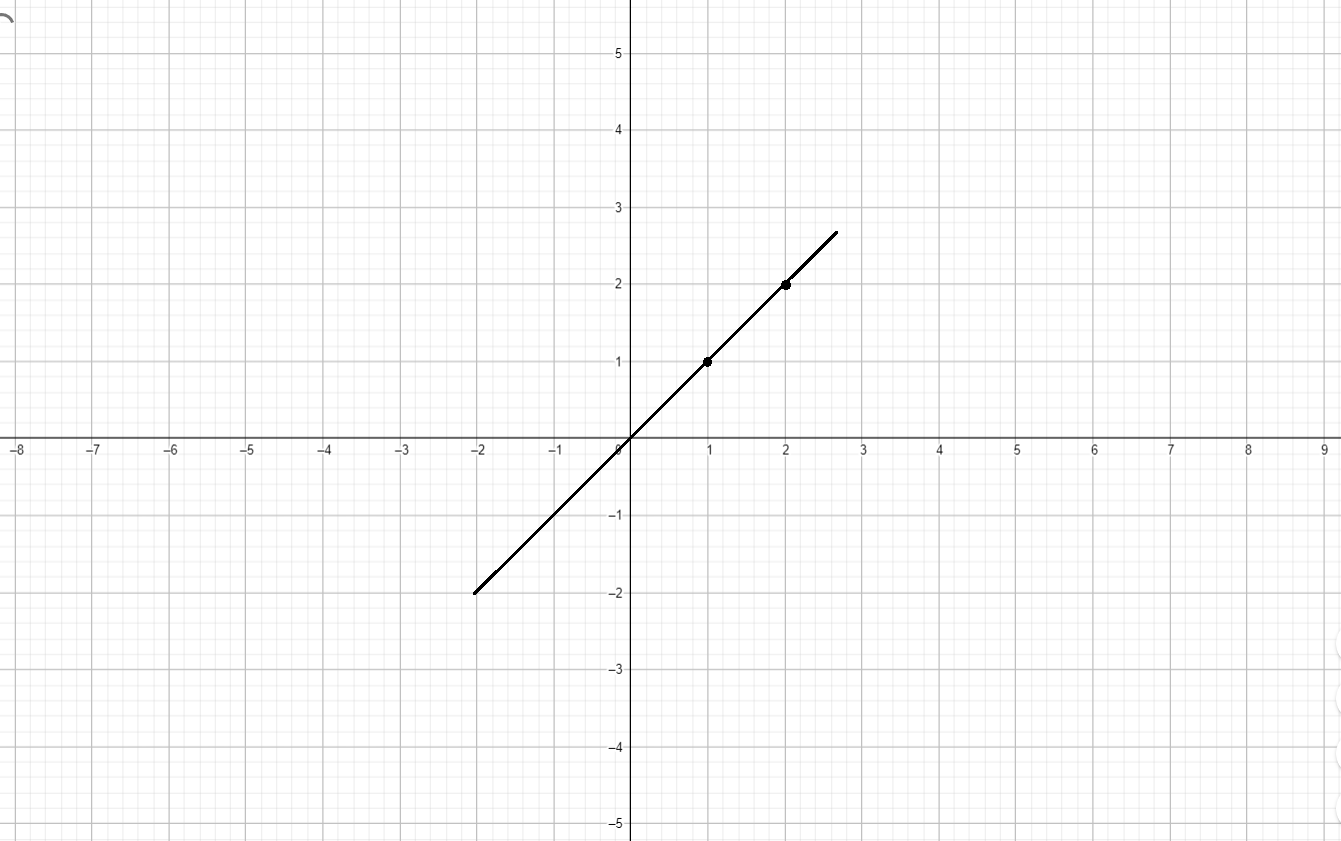ГДЗ по Алгебре 10 Класс Номер 10.28 Профильный Уровень Мордкович — Подробные Ответы

Построить график функции $y=f(g(x)),\; если:$

а) $f(x) = x^2$ и $g(x) = \sqrt{x}$;

б) $f(x) = -x^2$ и $g(x) = \sqrt{-x}$;

в) $f(x) = x^2$ и $g(x) = -\sqrt{x}$;

г) $f(x) = -x^2$ и $g(x)=-\sqrt{-x}$

Построить график функции $y = f(g(x))$;

а) $f(x) = x^2$ и $g(x) = \sqrt{x}$;

Искомая функция:

$$y = f(g(x)) = f(\sqrt{x}) = (\sqrt{x})^2 = x;$$

Выражение имеет смысл при:

$$x \geq 0;$$

График функции:

б) $f(x) = -x^2$ и $g(x) = \sqrt{-x}$;

Искомая функция:

$$y = f(g(x)) = f(\sqrt{-x}) = -(\sqrt{-x})^2 = -(-x) = x;$$

Выражение имеет смысл при:

$$-x \geq 0 \quad \Rightarrow \quad x \leq 0;$$

График функции:

в) $f(x) = x^2$ и $g(x) = -\sqrt{x}$;

Искомая функция:

$$y = f(g(x)) = f(-\sqrt{x}) = (-\sqrt{x})^2 = (\sqrt{x})^2 = x;$$

Выражение имеет смысл при:

$$x \geq 0;$$

График функции:

г) $f(x) = -x^2$ и $g(x) = -\sqrt{-x}$;

Искомая функция:

$$y = f(g(x)) = f(-\sqrt{-x}) = -(-\sqrt{-x})^2 = -(\sqrt{-x})^2 = -(-x) = x;$$

Выражение имеет смысл при:

$$-x \geq 0 \quad \Rightarrow \quad x \leq 0;$$

График функции:

Построить график функции $y = f(g(x))$;

а) $f(x) = x^2$ и $g(x) = \sqrt{x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Даны функции:

• $f(x) = x^2$
• $g(x) = \sqrt{x}$

Нам нужно вычислить композицию $f(g(x))$, то есть $f$ от $g(x)$:

$$f(g(x)) = f(\sqrt{x}).$$

Подставляем выражение для $g(x)$ в функцию $f(x)$:

$$f(\sqrt{x}) = (\sqrt{x})^2 = x.$$

Итак, получаем, что результат композиции $f(g(x))$ — это просто $x$. То есть, выражение для функции $y = f(g(x))$ сводится к $y = x$.

Шаг 2: Условия, при которых выражение имеет смысл:

Для того чтобы функция $g(x) = \sqrt{x}$ была определена, $x$ должно быть неотрицательным, то есть $x \geq 0$.

Следовательно, выражение для $f(g(x)) = x$ имеет смысл только при $x \geq 0$.

Шаг 3: График функции:

Поскольку результат композиции — это просто $y = x$, то график функции представляет собой прямую линию с угловым коэффициентом 1, которая проходит через начало координат. Это стандартная диагональ $y = x$, которая существует только для значений $x \geq 0$.

б) $f(x) = -x^2$ и $g(x) = \sqrt{-x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Даны функции:

• $f(x) = -x^2$
• $g(x) = \sqrt{-x}$

Нам нужно вычислить композицию $f(g(x))$, то есть $f$ от $g(x)$:

$$f(g(x)) = f(\sqrt{-x}).$$

Подставляем выражение для $g(x)$ в функцию $f(x)$:

$$f(\sqrt{-x}) = -(\sqrt{-x})^2 = -(-x) = x.$$

Итак, получаем, что результат композиции $f(g(x)) = x$.

Шаг 2: Условия, при которых выражение имеет смысл:

Для того чтобы функция $g(x) = \sqrt{-x}$ была определена, подкоренное выражение должно быть неотрицательным, то есть $-x \geq 0$, или $x \leq 0$.

Следовательно, выражение для $f(g(x)) = x$ имеет смысл только при $x \leq 0$.

Шаг 3: График функции:

Так как результат композиции — это просто $y = x$, график функции будет прямой линией с угловым коэффициентом 1, но только для значений $x \leq 0$. Это будет часть прямой $y = x$ на отрезке $x \leq 0$.

в) $f(x) = x^2$ и $g(x) = -\sqrt{x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Даны функции:

• $f(x) = x^2$
• $g(x) = -\sqrt{x}$

Нам нужно вычислить композицию $f(g(x))$, то есть $f$ от $g(x)$:

$$f(g(x)) = f(-\sqrt{x}).$$

Подставляем выражение для $g(x)$ в функцию $f(x)$:

$$f(-\sqrt{x}) = (-\sqrt{x})^2 = (\sqrt{x})^2 = x.$$

Таким образом, результат композиции $f(g(x)) = x$.

Шаг 2: Условия, при которых выражение имеет смысл:

Для того чтобы функция $g(x) = -\sqrt{x}$ была определена, подкоренное выражение должно быть неотрицательным, то есть $x \geq 0$.

Следовательно, выражение для $f(g(x)) = x$ имеет смысл только при $x \geq 0$.

Шаг 3: График функции:

Поскольку результат композиции — это $y = x$, график будет прямой линией с угловым коэффициентом 1, которая проходит через начало координат, и существует только для значений $x \geq 0$.

г) $f(x) = -x^2$ и $g(x) = -\sqrt{-x}$;

Шаг 1: Составление выражения для $f(g(x))$:

Даны функции:

• $f(x) = -x^2$
• $g(x) = -\sqrt{-x}$

Нам нужно вычислить композицию $f(g(x))$, то есть $f$ от $g(x)$:

$$f(g(x)) = f(-\sqrt{-x}).$$

Подставляем выражение для $g(x)$ в функцию $f(x)$:

$$f(-\sqrt{-x}) = -(-\sqrt{-x})^2 = -(\sqrt{-x})^2 = -(-x) = x.$$

Таким образом, результат композиции $f(g(x)) = x$.

Шаг 2: Условия, при которых выражение имеет смысл:

Для того чтобы функция $g(x) = -\sqrt{-x}$ была определена, подкоренное выражение должно быть неотрицательным, то есть $-x \geq 0$, или $x \leq 0$.

Следовательно, выражение для $f(g(x)) = x$ имеет смысл только при $x \leq 0$.

Шаг 3: График функции:

Так как результат композиции — это $y = x$, график будет прямой линией с угловым коэффициентом 1, но только для значений $x \leq 0$. Это будет часть прямой $y = x$ на отрезке $x \leq 0$.