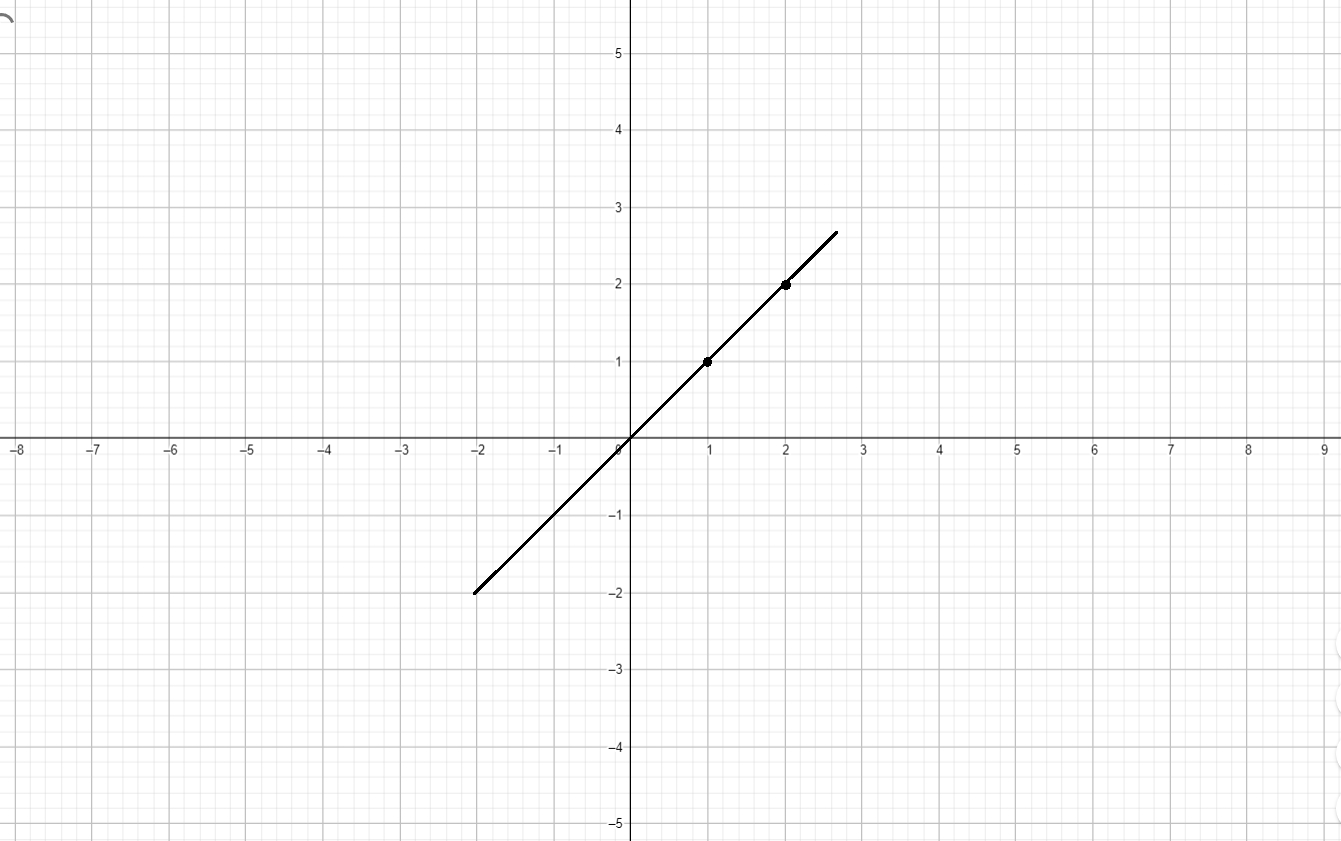ГДЗ по Алгебре 10 Класс Номер 10.29 Профильный Уровень Мордкович — Подробные Ответы

а) $f(x) = x^2 + 1$ и $g(x) = \sqrt{x — 1}$;

б) $f(x) = 3 — 0.5x^2$ и $g(x) = \sqrt{6 — 2x}$;

в) $f(x) = x^2 — 2$ и $g(x) = \sqrt{x + 2}$;

г) $f(x) = 8 — 2x^2$ и $g(x) = -\sqrt{4 — 0.5x}$

Построить график функции $y = f(g(x))$;

а) $f(x) = x^2 + 1$ и $g(x) = \sqrt{x — 1}$;

Искомая функция:

$$y = f(g(x)) = f(\sqrt{x — 1}) = (\sqrt{x — 1})^2 + 1 = x — 1 + 1 = x;$$

Выражение имеет смысл при:

$$x — 1 \geq 0 \quad \Rightarrow \quad x \geq 1;$$

График функции:

б) $f(x) = 3 — 0.5x^2$ и $g(x) = \sqrt{6 — 2x}$;

Искомая функция:

$$y = f(g(x)) = f(\sqrt{6 — 2x}) = 3 — 0.5(\sqrt{6 — 2x})^2;$$ $$y = 3 — 0.5(6 — 2x) = 3 — 3 + x = x;$$

Выражение имеет смысл при:

$$6 — 2x \geq 0 \quad \Rightarrow \quad 2x \leq 6 \quad \Rightarrow \quad x \leq 3;$$

График функции:

в) $f(x) = x^2 — 2$ и $g(x) = \sqrt{x + 2}$;

Искомая функция:

$$y = f(g(x)) = f(\sqrt{x + 2}) = (\sqrt{x + 2})^2 — 2 = x + 2 — 2 = x;$$

Выражение имеет смысл при:

$$x + 2 \geq 0 \quad \Rightarrow \quad x \geq -2;$$

График функции:

г) $f(x) = 8 — 2x^2$ и $g(x) = -\sqrt{4 — 0.5x}$;

Искомая функция:

$$y = f(g(x)) = f(-\sqrt{4 — 0.5x}) = 8 — 2(-\sqrt{4 — 0.5x})^2;$$ $$y = 8 — 2(4 — 0.5x) = 8 — 8 + x = x;$$

Выражение имеет смысл при:

$$4 — 0.5x \geq 0 \quad \Rightarrow \quad 0.5x \leq 4 \quad \Rightarrow \quad x \leq 8;$$

График функции:

Построить график функции $y = f(g(x))$

Для каждого случая нужно провести подробное решение, которое включает:

• Формулировку искомой функции.
• Условия, при которых выражение имеет смысл.
• Построение графика функции.

а) $f(x) = x^2 + 1$ и $g(x) = \sqrt{x — 1}$

1) Искомая функция:

Искомая функция — это композиция функций $f(g(x))$. Для этого подставим выражение для $g(x)$ в $f(x)$.

$$y = f(g(x)) = f(\sqrt{x — 1}) = (\sqrt{x — 1})^2 + 1$$

Упростим выражение:

$$(\sqrt{x — 1})^2 = x — 1$$

Тогда:

$$y = x — 1 + 1 = x$$

Итак, искомая функция: $y = x$.

2) Условия, при которых выражение имеет смысл:

Чтобы выражение $g(x) = \sqrt{x — 1}$ имело смысл, подкоренное выражение должно быть неотрицательным:

$$x — 1 \geq 0 \quad \Rightarrow \quad x \geq 1$$

Таким образом, функция имеет смысл при $x \geq 1$.

3) График функции:

Функция $y = x$ — это прямая линия с угловым коэффициентом 1, которая начинается с точки $x = 1$ на оси $x$ и идет вверх с углом 45 градусов.

График функции будет представлен прямой, начиная с $x = 1$.

б) $f(x) = 3 — 0.5x^2$ и $g(x) = \sqrt{6 — 2x}$

1) Искомая функция:

Подставим выражение для $g(x)$ в $f(x)$.

$$y = f(g(x)) = f(\sqrt{6 — 2x}) = 3 — 0.5(\sqrt{6 — 2x})^2$$

Упростим выражение:

$$(\sqrt{6 — 2x})^2 = 6 — 2x$$

Тогда:

$$y = 3 — 0.5(6 — 2x) = 3 — 3 + x = x$$

Итак, искомая функция: $y = x$.

2) Условия, при которых выражение имеет смысл:

Чтобы выражение $g(x) = \sqrt{6 — 2x}$ имело смысл, подкоренное выражение должно быть неотрицательным:

$$6 — 2x \geq 0 \quad \Rightarrow \quad 2x \leq 6 \quad \Rightarrow \quad x \leq 3$$

Таким образом, функция имеет смысл при $x \leq 3$.

3) График функции:

Функция $y = x$ — это прямая линия, как и в предыдущем случае. График будет представлен прямой, но на этот раз функция определена только для $x \leq 3$.

в) $f(x) = x^2 — 2$ и $g(x) = \sqrt{x + 2}$

1) Искомая функция:

Подставим выражение для $g(x)$ в $f(x)$.

$$y = f(g(x)) = f(\sqrt{x + 2}) = (\sqrt{x + 2})^2 — 2$$

Упростим выражение:

$$(\sqrt{x + 2})^2 = x + 2$$

Тогда:

$$y = x + 2 — 2 = x$$

Итак, искомая функция: $y = x$.

2) Условия, при которых выражение имеет смысл:

Чтобы выражение $g(x) = \sqrt{x + 2}$ имело смысл, подкоренное выражение должно быть неотрицательным:

$$x + 2 \geq 0 \quad \Rightarrow \quad x \geq -2$$

Таким образом, функция имеет смысл при $x \geq -2$.

3) График функции:

Функция $y = x$ — это прямая линия. График функции будет представлен прямой, начиная с $x = -2$ на оси $x$ и идет вверх с углом 45 градусов.

г) $f(x) = 8 — 2x^2$ и $g(x) = -\sqrt{4 — 0.5x}$

1) Искомая функция:

Подставим выражение для $g(x)$ в $f(x)$.

$$y = f(g(x)) = f(-\sqrt{4 — 0.5x}) = 8 — 2(-\sqrt{4 — 0.5x})^2$$

Упростим выражение:

$$(-\sqrt{4 — 0.5x})^2 = 4 — 0.5x$$

Тогда:

$$y = 8 — 2(4 — 0.5x) = 8 — 8 + x = x$$

Итак, искомая функция: $y = x$.

2) Условия, при которых выражение имеет смысл:

Чтобы выражение $g(x) = -\sqrt{4 — 0.5x}$ имело смысл, подкоренное выражение должно быть неотрицательным:

$$4 — 0.5x \geq 0 \quad \Rightarrow \quad 0.5x \leq 4 \quad \Rightarrow \quad x \leq 8$$

Таким образом, функция имеет смысл при $x \leq 8$.

3) График функции:

Функция $y = x$ — это прямая линия, как и в предыдущих случаях. График будет представлен прямой, но на этот раз функция определена только для $x \leq 8$.

Заключение:

Для всех четырех случаев мы получили линейную функцию $y = x$, которая является прямой, но с ограничениями на область определения. В зависимости от условий, график функции будет частью прямой $y = x$, ограниченной соответствующими интервалами:

• Для а): $x \geq 1$
• Для б): $x \leq 3$
• Для в): $x \geq -2$
• Для г): $x \leq 8$