ГДЗ по Алгебре 10 Класс Номер 10.3 Профильный Уровень Мордкович — Подробные Ответы

Для функции, заданной графически, укажите область определения и выясните, имеет эта функция в своей обла-сти определения обратную функцию или нет; в случае положительного ответа постройте эскиз графика обратной функции:

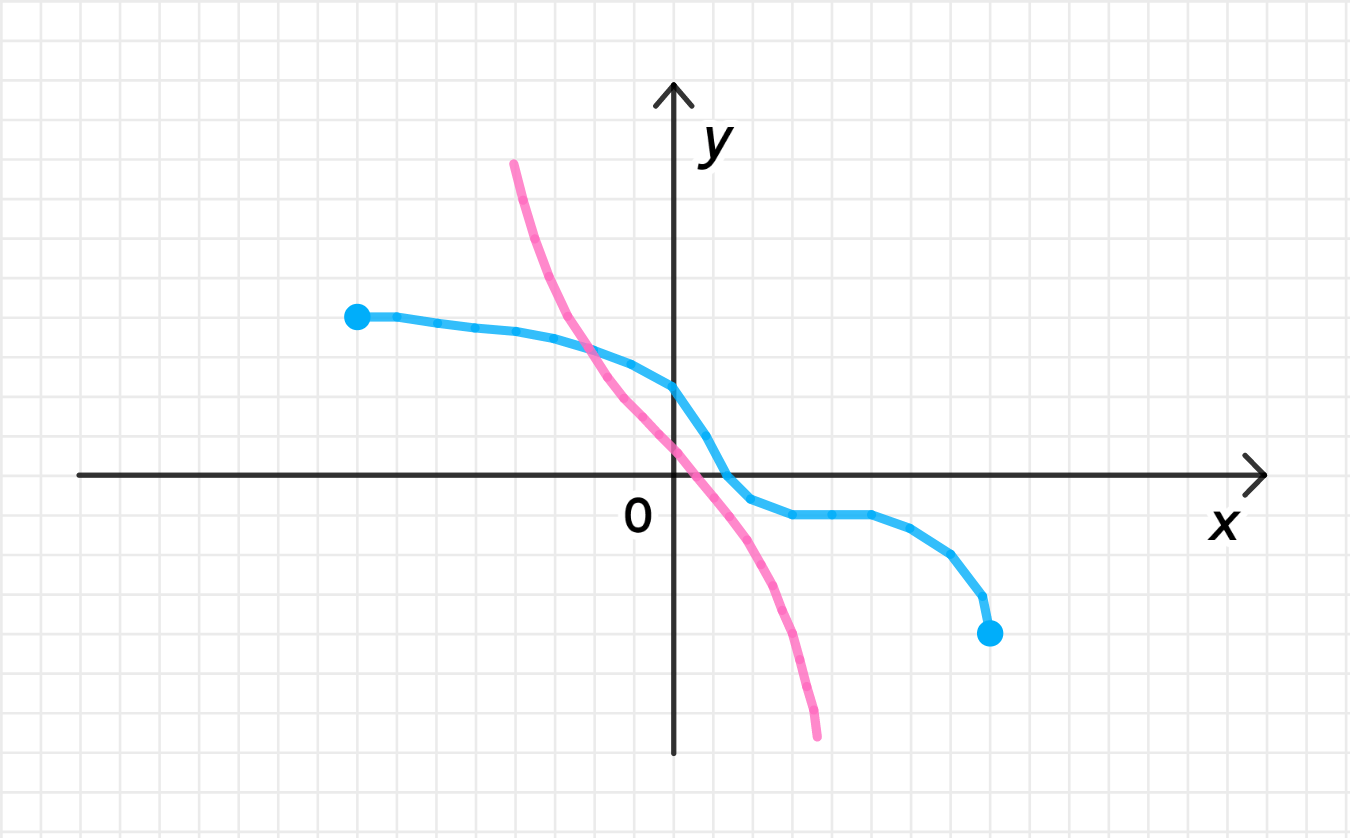
а) рис. 34;

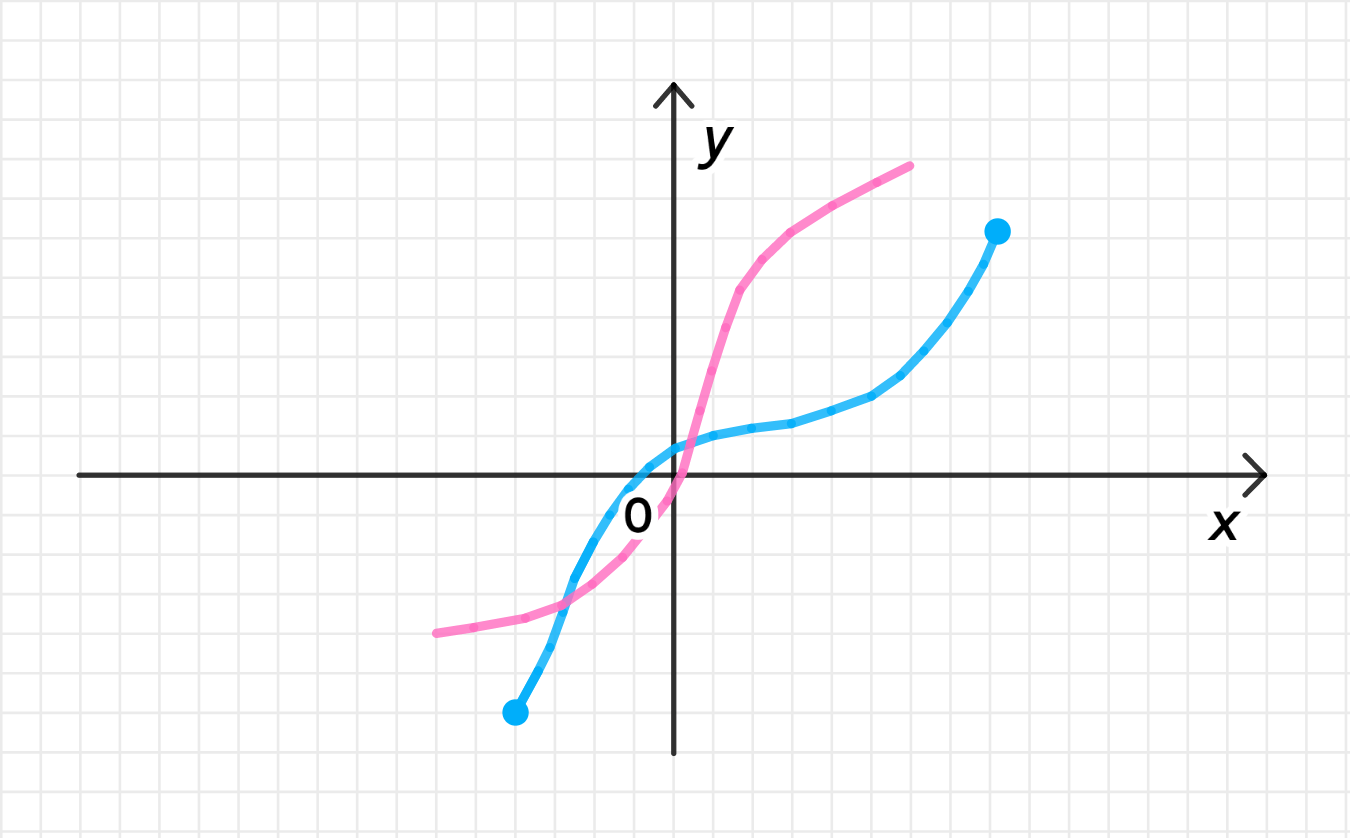
б) рис. 35;

в) рис. 36;

г) рис. 37.

Функция обратима на множестве $X$, если любое свое значение она принимает только в одной точке на $X$;
Графики взаимообратных функций симметричны относительно прямой $y = x$;

а) Рисунок 34;

1. Область определения функции: $D(f) = [-4; 4]$;
2. Функция монотонно убывает на $D(f)$, значит она обратима;
3. График обратной функции:

б) Рисунок 35;

1. Область определения функции: $D(f) = [-4; 4]$;
2. При $x = 2,5$ и $x = 3,5$, функция принимает одно и то же значение $y = -1$, следовательно, она не является обратимой;

в) Рисунок 36;

1. Область определения функции: $D(f) = [-4; 3]$;
2. При $x = -4$ и $x = 2$, функция принимает одно и то же значение $y = -2$, следовательно, она не является обратимой;

г) Рисунок 37;

1. Область определения функции: $D(f) = [-2; 4]$;
2. Функция монотонно убывает на $D(f)$, значит она обратима;
3. График обратной функции:

Определение обратимости функции:

Функция называется обратимой на множестве $X$, если для каждого значения функции существует только одна соответствующая точка на множестве $X$. Это означает, что функция не может принимать одно и то же значение в двух или более точках области определения $X$.

Графики взаимно обратных функций симметричны относительно прямой $y = x$. То есть, если $f$ — функция и $f^{-1}$ — ее обратная функция, то графики этих функций будут зеркальными отражениями друг друга относительно прямой $y = x$.

Рассмотрим каждый рисунок и детально разберемся, является ли функция обратимой.

а) Рисунок 34

Область определения функции: $D(f) = [-4; 4]$.

Это означает, что функция $f$ определена для всех значений $x$ от $-4$ до $4$, включая эти значения.

Функция монотонно убывает на $D(f)$, значит она обратима:

Чтобы функция была обратимой, она должна быть монотонной (или строго возрастать, или строго убывать) на своем интервале определения. В данном случае функция монотонно убывает, то есть, с увеличением $x$ значение функции $f(x)$ строго уменьшается.

Когда функция монотонна, она не может принимать одно и то же значение в разных точках области определения. Это позволяет заключить, что функция имеет обратную функцию на $D(f)$.

График обратной функции:

График обратной функции будет симметричен графику исходной функции относительно прямой $y = x$. Это можно проиллюстрировать на графике, который показан в виде изображения для данного пункта задачи.

б) Рисунок 35

Область определения функции: $D(f) = [-4; 4]$.

Область определения функции остается такой же, как и в предыдущем случае: функция определена для всех значений $x$ от $-4$ до $4$.

При $x = 2,5$ и $x = 3,5$, функция принимает одно и то же значение $y = -1$, следовательно, она не является обратимой:

Чтобы функция была обратимой, она должна принимать уникальное значение для каждой точки из области определения. Однако, как указано в пункте, для $x = 2,5$ и $x = 3,5$ функция принимает одно и то же значение $y = -1$.

Это нарушение условия уникальности значений означает, что функция не является инъективной (неоднозначной), а значит, она не имеет обратной функции.

Таким образом, в данном случае функция не обратима.

в) Рисунок 36

Область определения функции: $D(f) = [-4; 3]$.

Область определения функции была изменена и теперь ограничена интервалом от $-4$ до $3$, то есть $f$ определена для всех значений $x$ от $-4$ до $3$.

При $x = -4$ и $x = 2$, функция принимает одно и то же значение $y = -2$, следовательно, она не является обратимой:

Аналогично пункту б, здесь также возникает проблема с тем, что функция принимает одно и то же значение для разных $x$. В данном случае, для $x = -4$ и $x = 2$, функция $f(x)$ принимает одинаковое значение $y = -2$.

Это также нарушает условие инъективности функции, и следовательно, она не является обратимой.

г) Рисунок 37

Область определения функции: $D(f) = [-2; 4]$.

Область определения функции на этот раз ограничена интервалом от $-2$ до $4$. То есть, функция определена для всех значений $x$ от $-2$ до $4$.

Функция монотонно убывает на $D(f)$, значит она обратима:

Как и в пункте а, функция на данном интервале монотонно убывает. То есть, при увеличении $x$ значение функции $f(x)$ строго уменьшается. Поскольку функция монотонна, она принимает уникальное значение для каждой точки из области определения, и следовательно, она обратима.

График обратной функции:

График обратной функции, как и в случае с пунктом а, будет симметричен графику исходной функции относительно прямой $y = x$.

Итоговое заключение:

• В пунктах а и г функции обратимы, так как они монотонно убывают на своих областях определения.
• В пунктах б и в функции не являются обратимыми, так как для некоторых значений $x$ функция принимает одно и то же значение $y$, что нарушает условие инъективности.