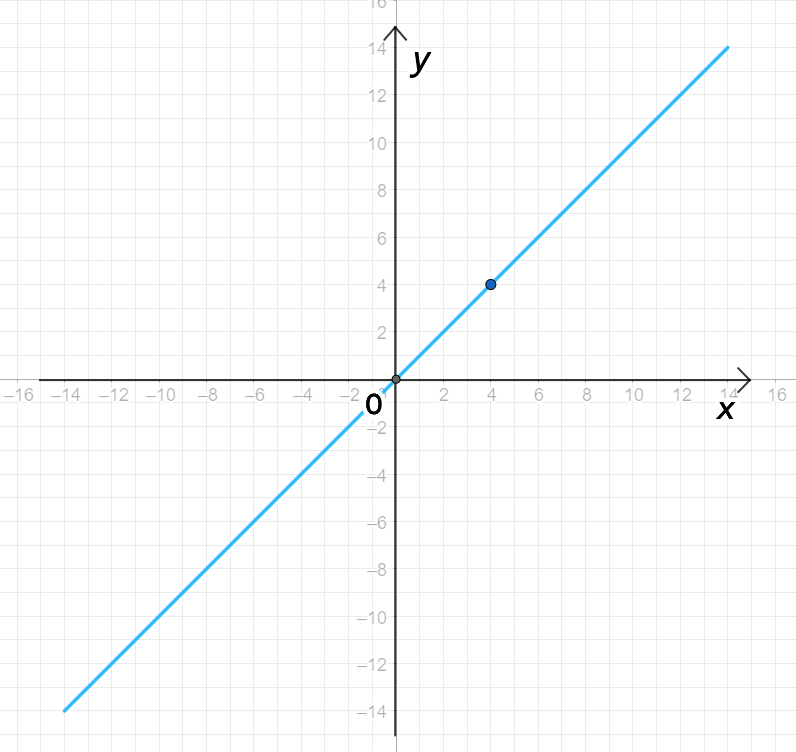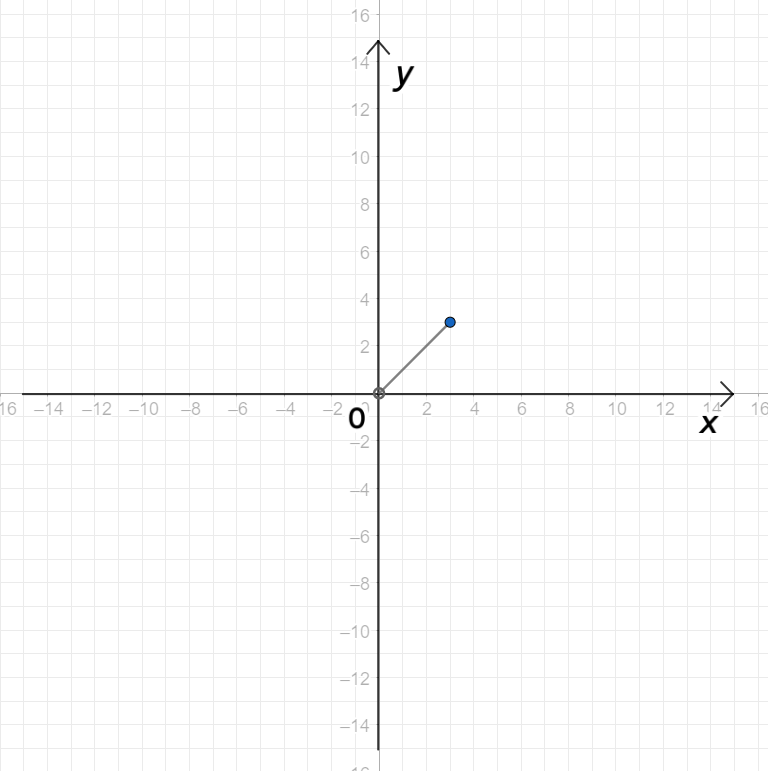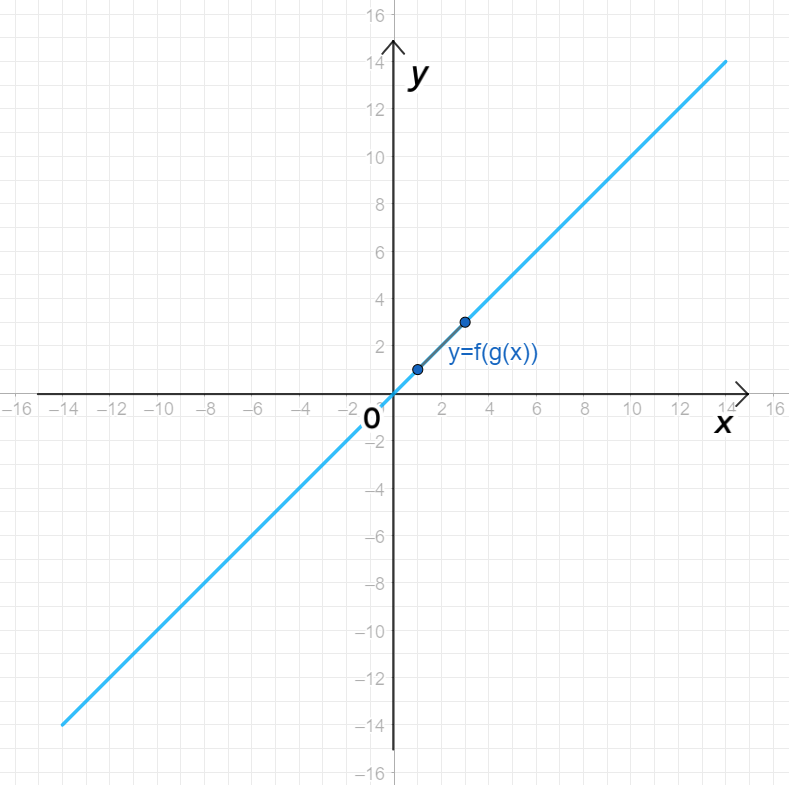Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 10.30 Профильный Уровень Мордкович — Подробные Ответы
Пусть у = f(x) и у = g(x) — взаимно-обратные функции. Постройте на двух различных чертежах графики функций у = f(g(x)) и у = g(f(x)), если:
а) D(f) = E(f) = R;
б) D(f) = E(f) = (0; 3];
в) D(f) = [1;3]; E(f) = R;
г) D(f) = [-2; 3]; E(f) = [-3; 2].
Функция всегда принимает только те значения, которые входят в область определения обратной ей функции, значит:
Если , тогда , где ;
Если , тогда , где ;
а) ;
Область определения второй функции:
;
График функции :
График функции :
б) ;
Область определения второй функции:
;
График функции :
График функции :
в) и ;
Область определения второй функции:
;
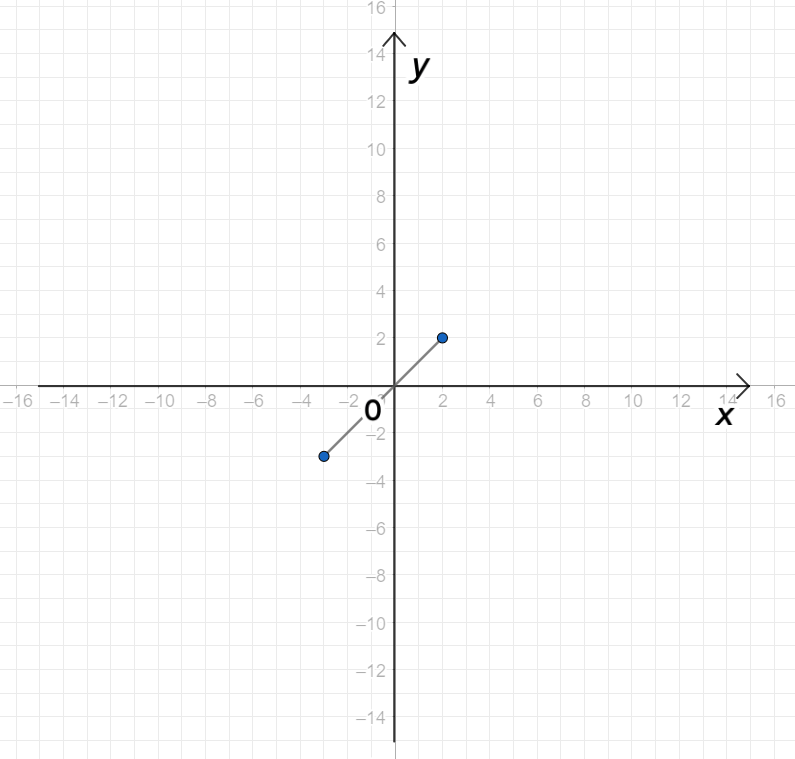
График функции :
График функции :
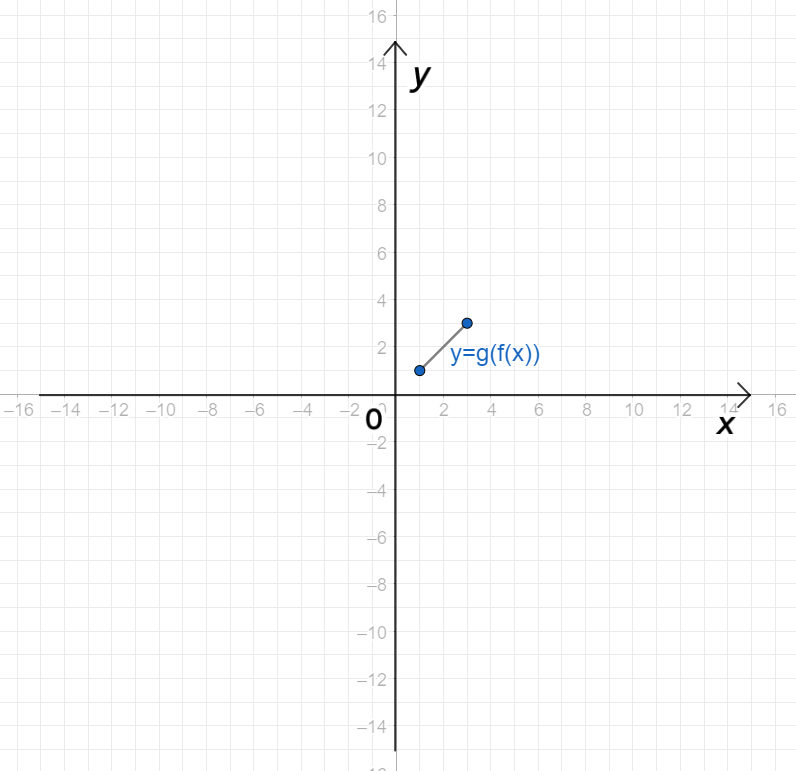
г) и ;
Область определения второй функции:
;
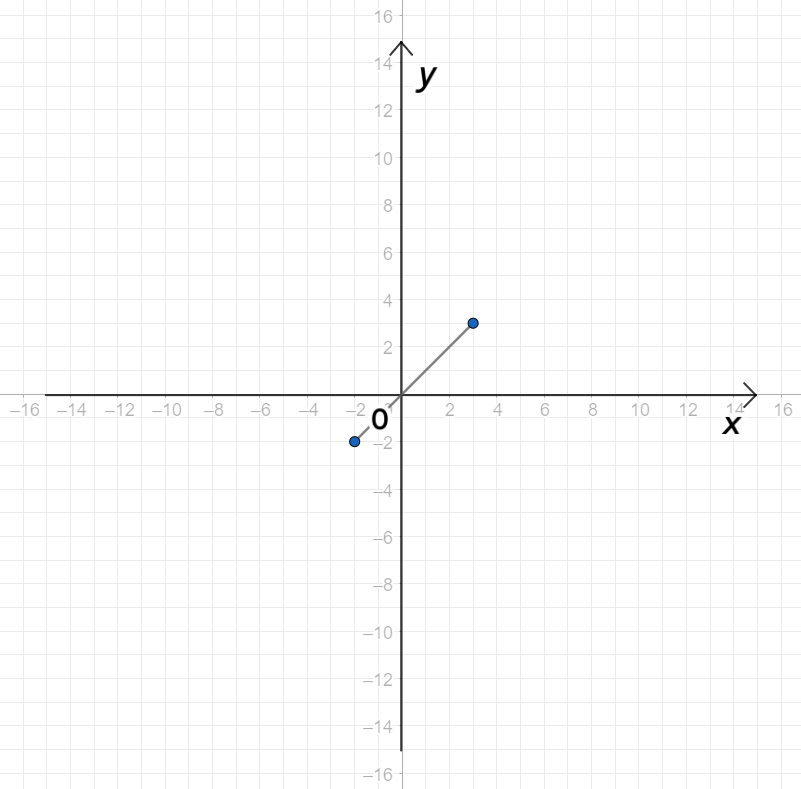
График функции :
График функции :
Общие положения:
- Функция означает, что значение функции подставляется в функцию .
- Функция означает, что значение функции подставляется в функцию .
Важные моменты:
- Функция определена, если , то есть, если результат функции попадает в область определения функции .
- Функция определена, если , то есть, если результат функции попадает в область определения функции .
Теперь перейдем к разбору каждого случая, предоставляя максимально подробное решение.
а)
- Область определения функции : , это означает, что функция определена для всех действительных чисел.
- Область значений функции : , это означает, что функция может принимать любые значения из множества действительных чисел.
1) Область определения второй функции:
Для функции мы знаем, что область определения должна быть такой, чтобы результат мог быть подставлен в функцию . Поскольку , то область определения функции может быть любая, то есть:
2) График функции :
Композиция будет определена для всех значений , так как область определения покрывает все действительные числа, а область определения тоже все числа. График будет зависеть от конкретных выражений для и , но так как области определения функций охватывают все числа, композиция будет работать для всех значений .
3) График функции :
Композиция будет также определена для всех , так как область определения , и определена на всем . Таким образом, как и в предыдущем случае, график будет представлять собой универсальную зависимость от , охватывая все действительные числа.
б)
- Область определения функции : , это означает, что функция определена только на интервале .
- Область значений функции : , это означает, что функция может принимать значения только в интервале .
1) Область определения второй функции:
Для того чтобы функция была определена, необходимо, чтобы попадал в область определения функции . Поскольку , то область определения функции будет ограничена этим интервалом. То есть:
2) График функции :
Поскольку область определения ограничена интервалом , то функция будет определена только на этом интервале. График функции будет зависеть от конкретных выражений для и , но он будет ограничен этим интервалом.
3) График функции :
Для того чтобы была определена, область определения должна попасть в область определения . Поскольку область определения — это , то область определения функции будет такой, что всегда попадал в . Таким образом, график будет определен на интервале .
в) и
- Область определения функции : , это означает, что функция определена только на интервале .
- Область значений функции : , это означает, что функция может принимать все значения из множества действительных чисел.
1) Область определения второй функции:
Для того чтобы была определена, необходимо, чтобы . Таким образом, область определения функции будет такой, что её значения попадали в интервал :
2) График функции :
График функции будет ограничен областью , поскольку принимает значения на этом интервале, и только тогда можно подставить их в функцию , которая определена только на этом интервале.
3) График функции :
Для того чтобы была определена, область значений должна попадать в область определения . Поскольку , а , график функции будет определен только тогда, когда , то есть на интервале .
г) и
- Область определения функции : , это означает, что функция определена только на интервале .
- Область значений функции : , это означает, что функция может принимать значения только в интервале .
1) Область определения второй функции:
Для того чтобы композиция была определена, необходимо, чтобы попадала в область определения функции . Поскольку , область определения должна быть внутри этого интервала:
2) График функции :
График функции будет ограничен интервалом , поскольку область определения и функция имеют ограничения на этом интервале.
3) График функции :
Для того чтобы была определена, область значений должна попадать в область определения . Поскольку и , график функции будет определен на интервале .