ГДЗ по Алгебре 10 Класс Номер 10.31 Профильный Уровень Мордкович — Подробные Ответы

Постройте на одном чертеже графики таких двух взаимно-обратных функций у = f(x) и у = g(x), чтобы уравнение f(x) = x:

а) имело один корень;

б) имело три корня;

в) имело бесконечно много корней;

г) не имело корней.

Построить графики таких двух взаимно обратных функций $y=f(x)$ и $y=g(x)$, чтобы уравнение $f(x)=x$:

а) Имело один корень:

График:

Формула:

$$f(x)=3x-2$$

б) Имело три корня:

График:

$y = g(x)$

Формула:

$$f(x)=x^3$$

в) Имело бесконечно много корней:

График:

Формула:

$$f(x)=\sin x+x$$

г) Не имело корней:

График:

Формула:

$$f(x)=x+2$$

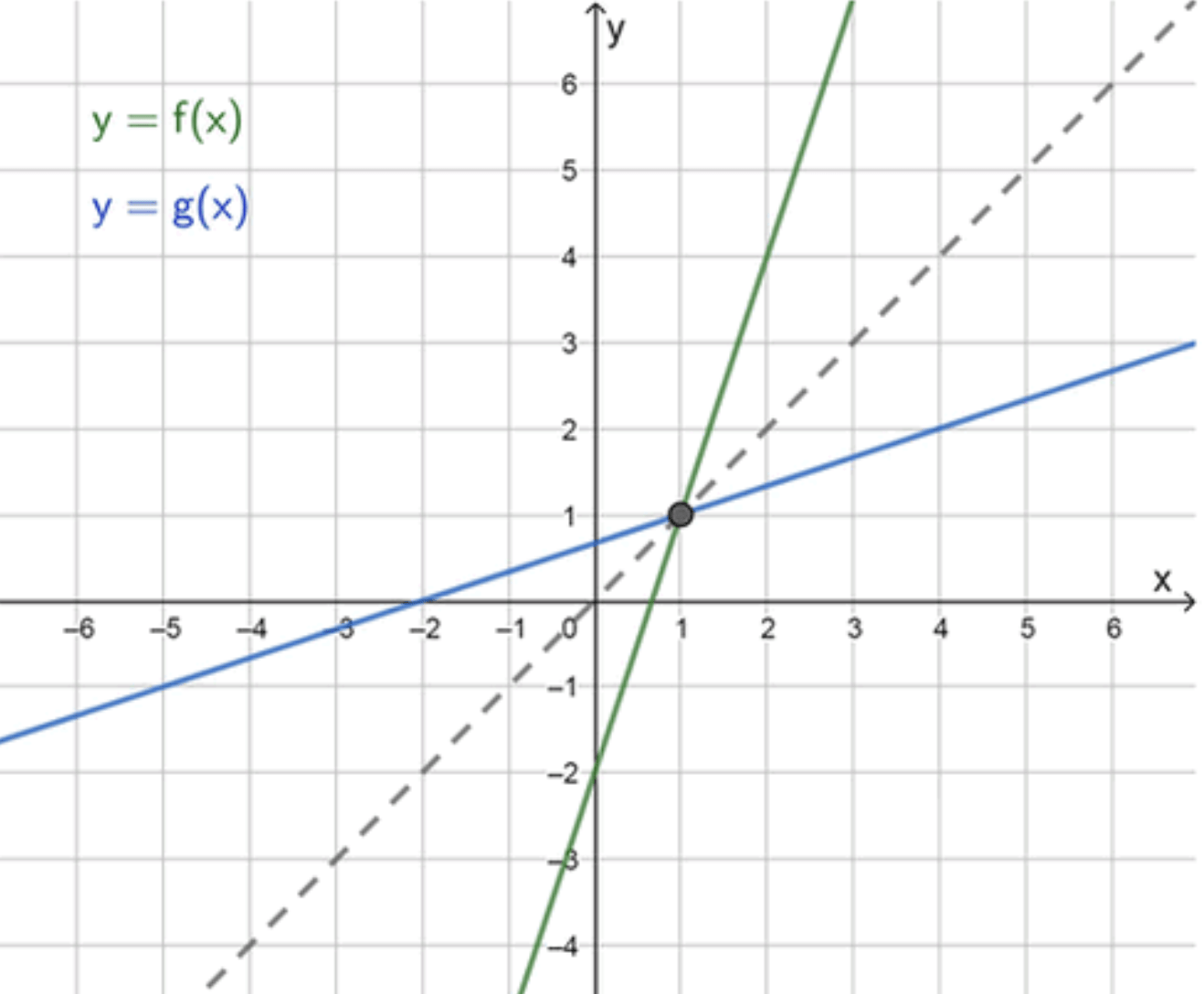
а) Уравнение $f(x)=x$ имеет один корень

1) Функция:

Для того чтобы уравнение $f(x)=x$ имело один корень, функция $f(x)$ должна быть линейной, и график этой функции должен пересекать прямую $y=x$ в одной точке.

Предложенная функция:

$$f(x)=3x-2$$

2) Анализ функции:

• Эта функция — линейная. Она имеет угловой коэффициент 3, что означает, что её график наклонён вверх.
• Уравнение $f(x)=x$ будет иметь один корень, если график $y=f(x)=3x-2$ и прямая $y=x$ пересекаются в одной точке. Для нахождения точки пересечения решим уравнение:

$$3x-2=x$$$$3x-x=2$$$$2x=2\Rightarrow x=1$$

Таким образом, уравнение $f(x)=x$ имеет один корень при $x=1$.

3) График функции:

• График функции $f(x)=3x-2$ — это прямая, которая пересекает ось $y$ в точке $(0,-2)$.
• Прямая $y=x$ — это также прямая, но с угловым коэффициентом 1, и её график проходит через начало координат.
• Графики этих функций пересекаются в точке $(1,1)$, что означает, что уравнение $f(x)=x$ имеет один корень.

График будет следующим: линия $y=3x-2$ пересекает прямую $y=x$ в точке $x=1$.

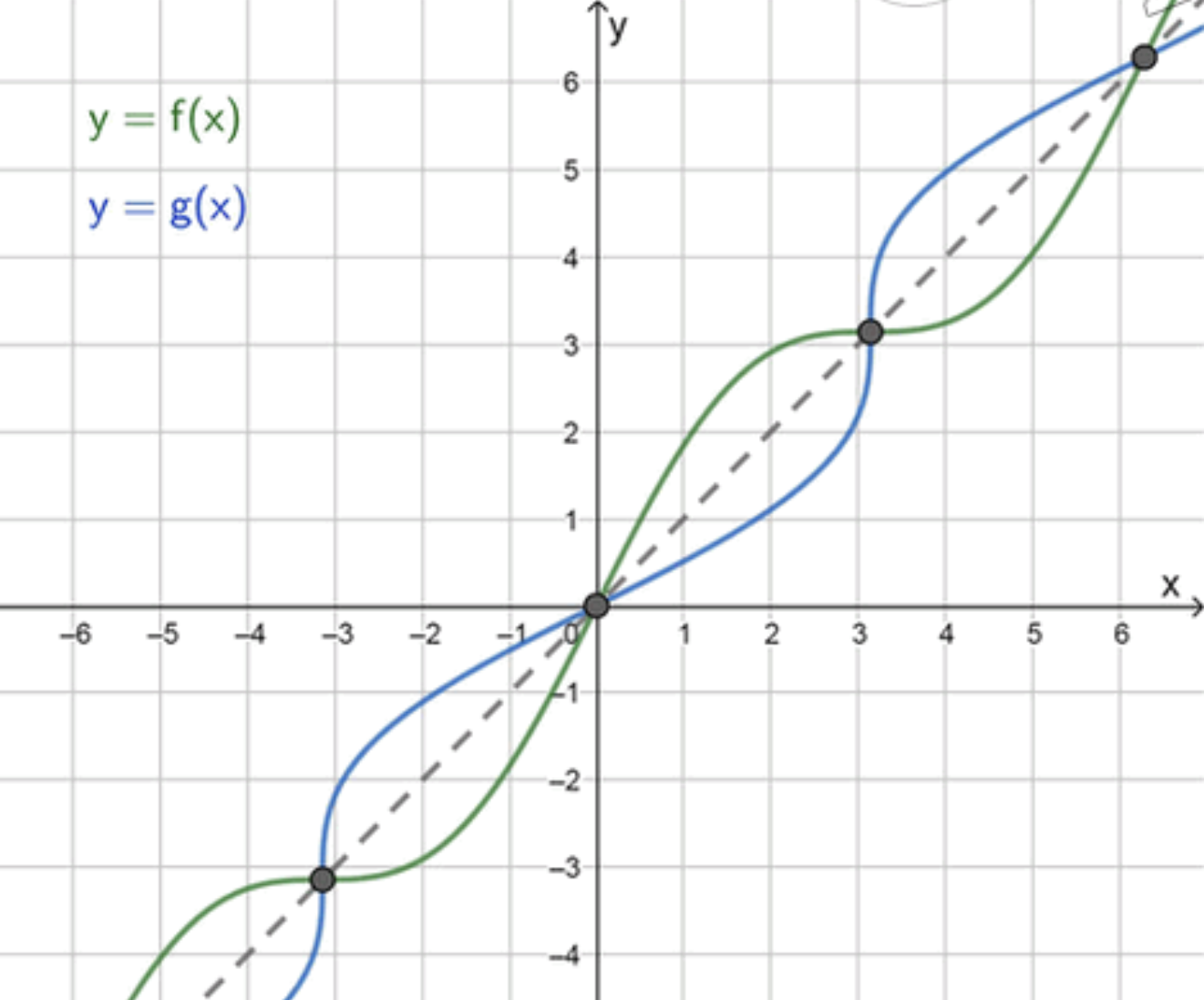
б) Уравнение $f(x)=x$ имеет три корня

1) Функция:

Для того чтобы уравнение $f(x)=x$ имело три корня, функция $f(x)$ должна быть кубической, и её график должен иметь три пересечения с прямой $y=x$.

Предложенная функция:

$$f(x)=x^3$$

2) Анализ функции:

• Это кубическая функция, график которой имеет характерный вид: S-образный.
• Уравнение $f(x)=x$ означает, что мы ищем пересечения графика функции $y=x^3$ с прямой $y=x$.
• Чтобы найти корни уравнения $x^3=x$, преобразуем его:

$$x^3=x\Rightarrow x^3-x=0\Rightarrow x(x^2-1)=0$$$$x(x-1)(x+1)=0$$

Это уравнение имеет три корня: $x=0,x=1,x=-1$.

Таким образом, уравнение $f(x)=x$ имеет три корня: $x=-1,x=0,x=1$.

3) График функции:

• График функции $f(x)=x^3$ представляет собой S-образную кривую, проходящую через начало координат.
• Прямая $y=x$ проходит через начало координат и имеет угол наклона 45 градусов.
• Эти две кривые пересекаются в трёх точках: $(-1,-1),(0,0),(1,1)$, что подтверждает наличие трёх корней.

График будет представлять собой кубическую кривую, пересекающую прямую $y=x$ в трёх точках.

в) Уравнение $f(x)=x$ имеет бесконечно много корней

1) Функция:

Для того чтобы уравнение $f(x)=x$ имело бесконечно много корней, функция $f(x)$ должна быть такой, что она всегда совпадает с прямой $y=x$ для всех значений $x$.

Предложенная функция:

$$f(x)=\sin x+x$$

2) Анализ функции:

• Эта функция состоит из суммы синусоидальной функции $\sin x$, которая колеблется между -1 и 1, и линейной функции $x$.
• Функция $f(x)=\sin x+x$ в определённом смысле будет всегда пересекаться с прямой $y=x$, потому что с увеличением $x$ линейная часть функции $x$ «перетягивает» функцию вверх, но колебания функции $\sin x$ создают регулярные пересечения с прямой $y=x$.
• Это означает, что уравнение $f(x)=x$ имеет бесконечно много корней, поскольку колебания функции $\sin x$ приводят к регулярным пересечениям с прямой $y=x$.

3) График функции:

• График функции $f(x)=\sin x+x$ будет представлять собой кривую, которая будет колебаться, но с постоянным увеличением вверх, так как добавляется линейная составляющая $x$.
• Прямая $y=x$ будет пересекать эту кривую бесконечное количество раз, так как функция будет регулярно пересекать прямую.

График будет представлять собой кривую с волнообразными колебаниями, которая бесконечно много раз пересекает прямую $y=x$.

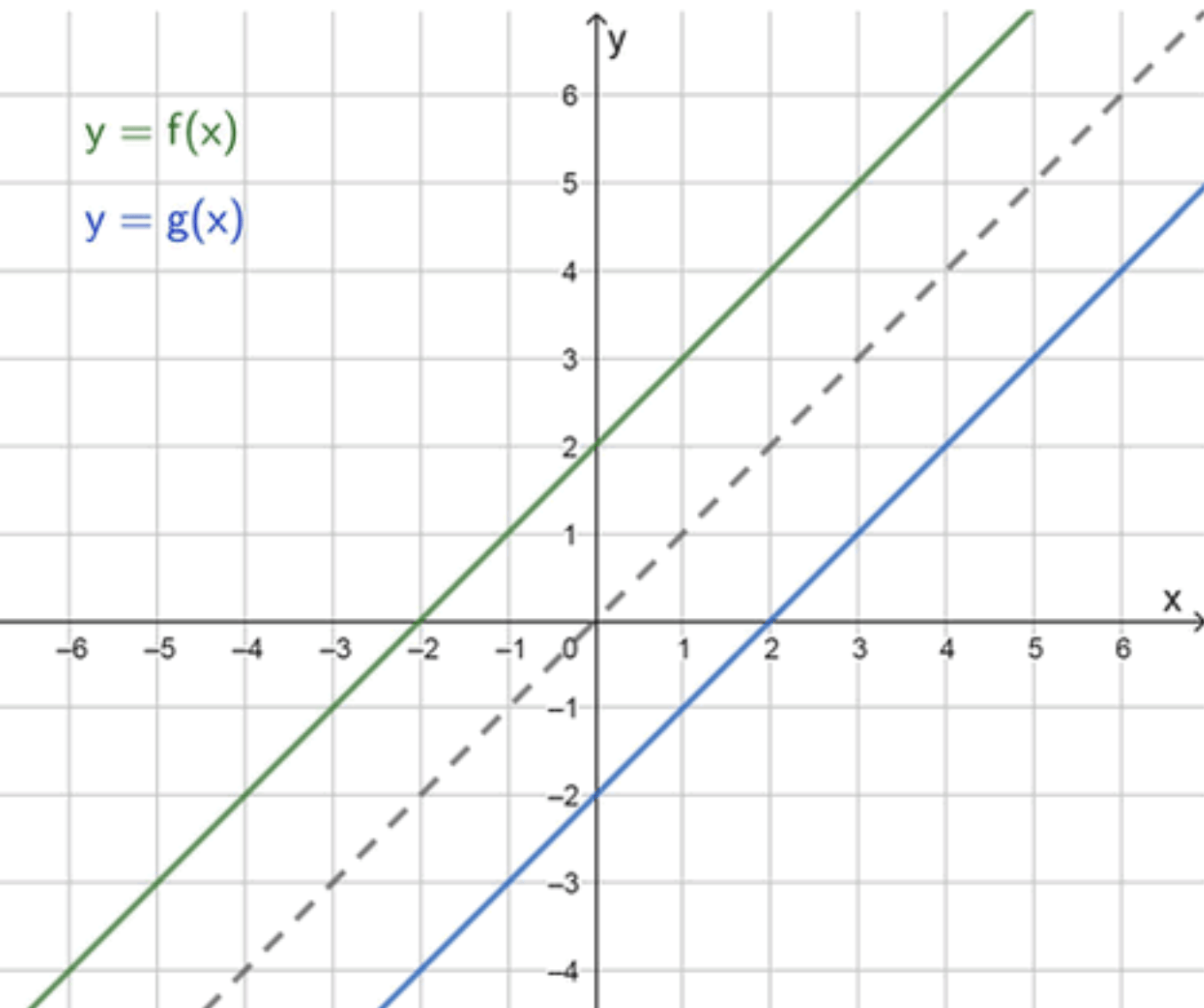
г) Уравнение $f(x)=x$ не имеет корней

1) Функция:

Для того чтобы уравнение $f(x)=x$ не имело корней, функция $f(x)$ должна быть такой, что её график никогда не пересекается с прямой $y=x$.

Предложенная функция:

$$f(x)=x+2$$

2) Анализ функции:

• Это линейная функция с угловым коэффициентом 1, но её график сдвинут вверх на 2 единицы.
• Уравнение $f(x)=x$ для этой функции будет:

$$x+2=x$$$$2=0$$

Это противоречие, следовательно, у этого уравнения нет решений, и функция $f(x)=x+2$ никогда не пересекает прямую $y=x$.

3) График функции:

• График функции $f(x)=x+2$ — это прямая, параллельная прямой $y=x$, но сдвинутая вверх на 2 единицы.
• Прямая $y=x$ и $y=x+2$ никогда не пересекаются, что означает отсутствие корней у уравнения $f(x)=x$.

График будет представлять собой две параллельные прямые, не имеющие точек пересечения.

Заключение:

а) Уравнение $f(x)=x$ имеет один корень, если функция $f(x)=3x-2$.

б) Уравнение $f(x)=x$ имеет три корня, если функция $f(x)=x^3$.

в) Уравнение $f(x)=x$ имеет бесконечно много корней, если функция $f(x)=\sin x+x$.

г) Уравнение $f(x)=x$ не имеет корней, если функция $f(x)=x+2$.