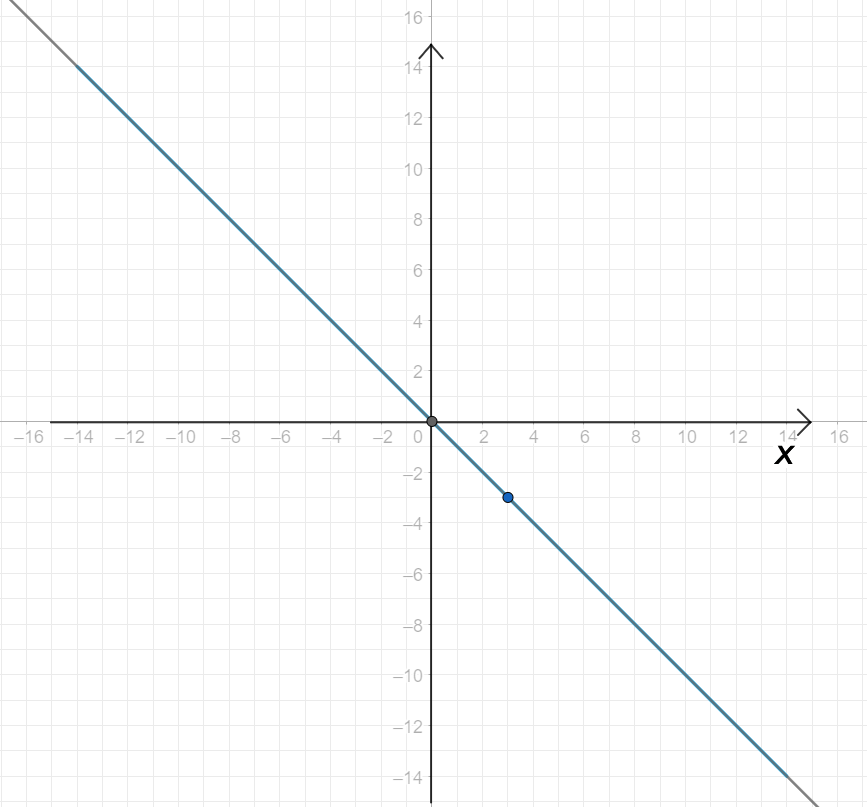ГДЗ по Алгебре 10 Класс Номер 10.32 Профильный Уровень Мордкович — Подробные Ответы

Постройте на одном чертеже графики таких двух взаимно-обратных функций у = f(x) и у = g(x) чтобы уравнение f(x) = g(x):

а) имело один корень;

б) имело три корня;

в) имело бесконечно много корней;

г) не имело корней.

Построить графики таких двух взаимно обратных функций $y = f(x)$ и $y = g(x)$, чтобы уравнение $f(x) = g(x)$:

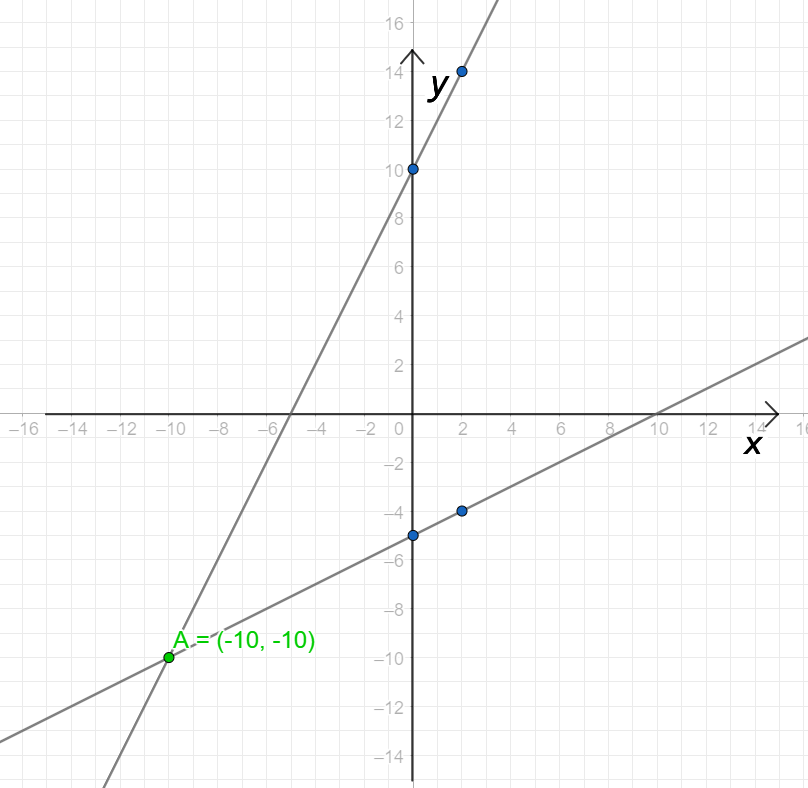
а) Имело один корень:

$$f(x) = 2x + 1;$$

б) Имело три корня:

$$f(x) = 0,25x^3;$$

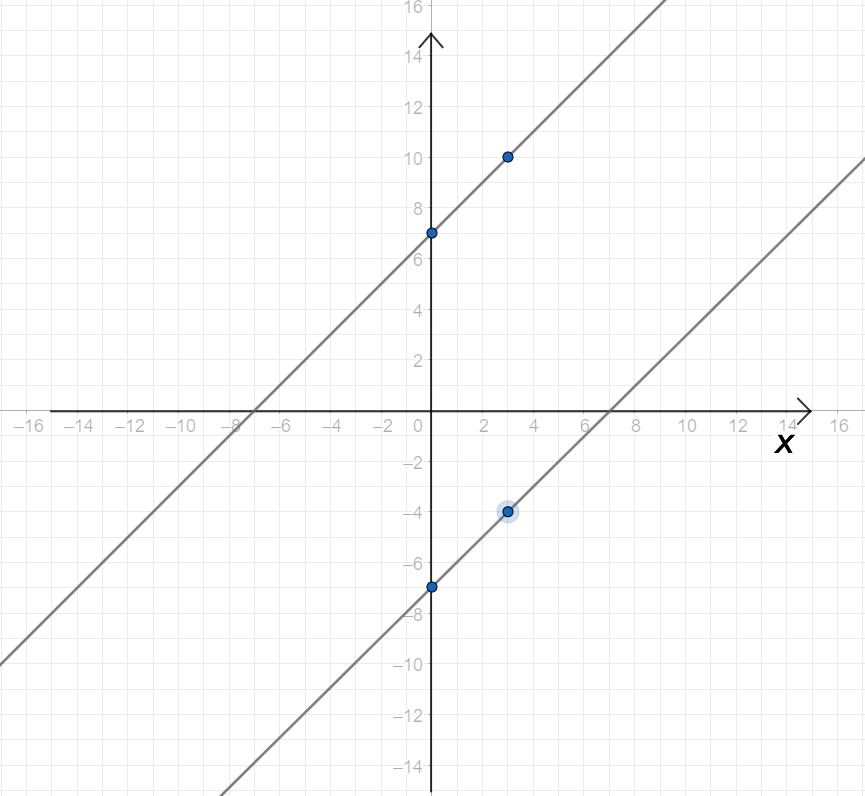
в) Имело бесконечно много корней:

$$f(x) = \cos x + x;$$

г) Не имело корней:

$$f(x) = \sqrt{x} — 5;$$

Основные теоретические положения:

Взаимные обратные функции:

Если функции $f(x)$ и $g(x)$ являются взаимно обратными, то выполняется условие:

$$g(f(x)) = x \quad \text{и} \quad f(g(x)) = x.$$

Это означает, что графики этих функций симметричны относительно прямой $y = x$.

Задача:

Построить графики двух взаимно обратных функций $y = f(x)$ и $y = g(x)$ так, чтобы уравнение $f(x) = g(x)$ имело заданное количество корней.

Случай (а): Уравнение $f(x) = g(x)$ имеет один корень.

Выбор функций:

Пусть функции $f(x)$ и $g(x)$ будут линейными. В таком случае взаимно обратными функциями могут быть функции вида:

$$f(x) = 2x + 1 \quad \text{и} \quad g(x) = \frac{x — 1}{2}.$$

Решение уравнения $f(x) = g(x)$:

Найдем решение уравнения $f(x) = g(x)$, то есть:

$$2x + 1 = \frac{x — 1}{2}.$$

Умножим обе стороны на 2, чтобы избавиться от дроби:

$$4x + 2 = x — 1.$$

Теперь перенесем все выражения, содержащие $x$, на одну сторону, а все константы — на другую:

$$4x — x = -1 — 2,$$ $$3x = -3.$$

Поделим обе стороны на 3:

$$x = -1.$$

Таким образом, уравнение $f(x) = g(x)$ имеет один корень $x = -1$.

Графики:

Графики функций $f(x)$ и $g(x)$ будут прямыми, пересекающимися в точке $(-1, f(-1)) = (-1, -1)$.

Случай (б): Уравнение $f(x) = g(x)$ имеет три корня.

Выбор функций:

Для этого случая можно выбрать функции, где $f(x)$ имеет кубическую форму, а $g(x)$ — также кубическую функцию, но с другой константой. Пусть:

$$f(x) = 0,25x^3 \quad \text{и} \quad g(x) = \sqrt[3]{x}.$$

Решение уравнения $f(x) = g(x)$:

Найдем решение уравнения:

$$0,25x^3 = \sqrt[3]{x}.$$

Возведем обе стороны в куб:

$$(0,25x^3)^3 = x.$$

Раскроем куб на левой стороне:

$$0,25^3 \cdot x^9 = x,$$ $$\frac{1}{64} x^9 = x.$$

Умножим обе стороны на 64:

$$x^9 = 64x.$$

Теперь вынесем $x$ за скобки:

$$x(x^8 — 64) = 0.$$

Решение:

$$x = 0 \quad \text{или} \quad x^8 = 64.$$

Из второго уравнения $x^8 = 64$ получаем:

$$x = \pm 2.$$

Таким образом, у уравнения $f(x) = g(x)$ есть три корня: $x = 0, -2, 2$.

Графики:

Графики этих функций будут пересекаться в трех точках: $x = -2$, $x = 0$, $x = 2$.

Случай (в): Уравнение $f(x) = g(x)$ имеет бесконечно много корней.

Выбор функций:

Для этого случая возьмем функцию с периодической частью. Пусть:

$$f(x) = \cos x + x \quad \text{и} \quad g(x) = x.$$

Решение уравнения $f(x) = g(x)$:

Найдем решение уравнения:

$$\cos x + x = x.$$

Упростим:

$$\cos x = 0.$$

Решение уравнения $\cos x = 0$ дает:

$$x = \frac{\pi}{2} + k\pi, \quad k \in \mathbb{Z}.$$

Таким образом, у уравнения $f(x) = g(x)$ бесконечно много решений, так как косинус принимает значение 0 в бесконечном числе точек.

Графики:

Графики этих функций будут пересекаться в точках, определяемых формулой $x = \frac{\pi}{2} + k\pi$, что приводит к бесконечному числу пересечений.

Случай (г): Уравнение $f(x) = g(x)$ не имеет корней.

Выбор функций:

В данном случае можно выбрать функцию с ограничениями по области определения. Пусть:

$$f(x) = \sqrt{x} — 5 \quad \text{и} \quad g(x) = x.$$

Решение уравнения $f(x) = g(x)$:

Найдем решение уравнения:

$$\sqrt{x} — 5 = x.$$

Переносим все выражения на одну сторону:

$$\sqrt{x} = x + 5.$$

Возводим обе стороны в квадрат:

$$x = (x + 5)^2.$$

Раскрываем скобки:

$$x = x^2 + 10x + 25.$$

Переносим все в одну сторону:

$$x^2 + 9x + 25 = 0.$$

Это квадратное уравнение. Проверим его дискриминант:

$$D = 9^2 — 4 \cdot 1 \cdot 25 = 81 — 100 = -19.$$

Дискриминант отрицателен, следовательно, у уравнения нет действительных корней.

Графики:

Графики функций не пересекаются, так как у уравнения нет действительных решений.