ГДЗ по Алгебре 10 Класс Номер 10.34 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции и определите, существует ли для нее обратная функция. Если да, то на том же чертеже постройте график обратной функции и задайте ее аналитически:

а) у = 3х + |x|;

б) у = x + 2|x|;

в) у = 2|х| — 5x;

г) у = 2x — 5|x|.

а) $y = 3x + |x|$;

Если $x \geq 0$, тогда:

$$y = 3x + x = 4x;$$

Если $x < 0$, тогда:

$$y = 3x — x = 2x;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c} x & -2 & 0 & 1 \\ \hline y & -4 & 0 & 4 \\ \end{array}$$

График функции:

Обратная функция существует:

$$x = 4y \quad => \quad y = \frac{x}{4};$$ $$x = 2y \quad => \quad y = \frac{x}{2};$$

Ответ:

$$y = \begin{cases} \frac{1}{4}x, & \text{если } x \geq 0 \\ \frac{1}{2}x, & \text{если } x < 0 \end{cases}.$$

б) $y = x + 2|x|$;

Если $x \geq 0$, тогда:

$$y = x + 2x = 3x;$$

Если $x < 0$, тогда:

$$y = x — 2x = -x;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c} x & -2 & 0 & 1 \\ \hline y & 2 & 0 & 3 \\ \end{array}$$

График функции:

Обратной функции не существует;

Ответ: нет.

в) $y = 2|x| — 5x$;

Если $x \geq 0$, тогда:

$$y = 2x — 5x = -3x;$$

Если $x < 0$, тогда:

$$y = -2x — 5x = -7x;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c} x & -1 & 0 & 1 \\ \hline y & 7 & 0 & -3 \\ \end{array}$$

График функции:

Обратная функция существует:

$$x = -3y \quad => \quad y = -\frac{x}{3};$$ $$x = -7y \quad => \quad y = -\frac{x}{7};$$

Ответ:

$$y = \begin{cases} -\frac{1}{3}x, & \text{если } x < 0 \\ -\frac{1}{7}x, & \text{если } x \geq 0 \end{cases}.$$

г) $y = 2x — 5|x|$;

Если $x \geq 0$, тогда:

$$y = 2x — 5x = -3x;$$

Если $x < 0$, тогда:

$$y = 2x + 5x = 7x;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c} x & -1 & 0 & 1 \\ \hline y & -7 & 0 & -3 \\ \end{array}$$

График функции:

Обратной функции не существует;

Ответ: нет.

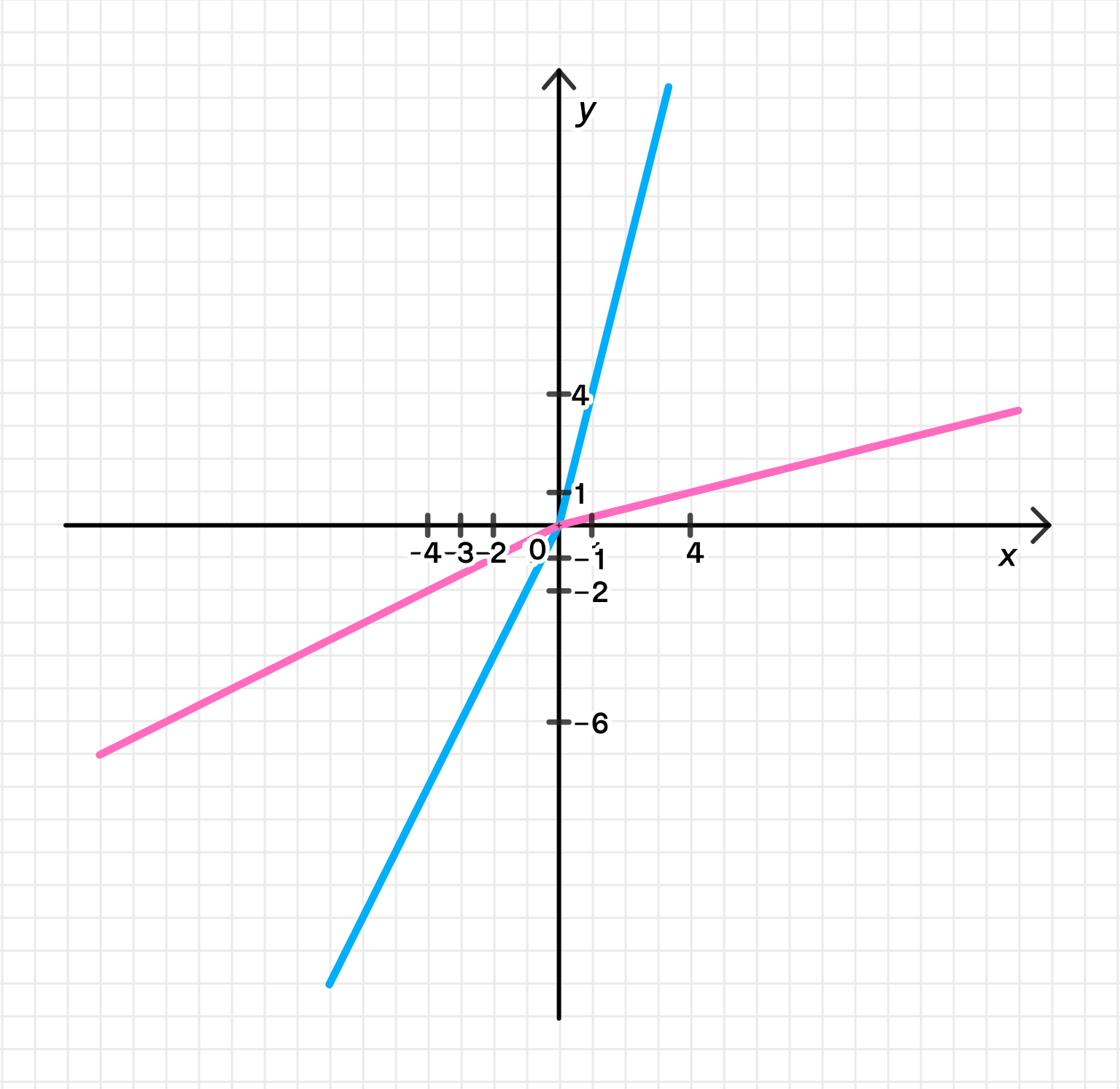
а) $y = 3x + |x|$

Разбиение на два случая:
Функция $y = 3x + |x|$ содержит абсолютную величину, поэтому её нужно рассматривать в двух случаях: когда $x \geq 0$ и $x < 0$.

• Если $x \geq 0$, то $|x| = x$, и функция примет вид:

  $$y = 3x + x = 4x.$$

  То есть, когда $x \geq 0$, функция линейная, с угловым коэффициентом 4.

• Если $x < 0$, то $|x| = -x$, и функция примет вид:

  $$y = 3x — x = 2x.$$

  В этом случае функция также линейная, но с угловым коэффициентом 2.

Координаты некоторых точек:
Для иллюстрации поведения функции выберем несколько значений $x$:

$$\begin{array}{c|c c c} x & -2 & 0 & 1 \\ \hline y & -4 & 0 & 4 \\ \end{array}$$

Для $x = -2$, $y = 3(-2) + 2 = -4$.
Для $x = 0$, $y = 3(0) + 0 = 0$.
Для $x = 1$, $y = 3(1) + 1 = 4$.

График функции:
График функции будет представлять собой две прямые: одну с угловым коэффициентом 4 для $x \geq 0$ и одну с угловым коэффициентом 2 для $x < 0$. Эти прямые соединяются в точке $x = 0$.

Нахождение обратной функции:
Теперь найдем обратную функцию для каждого из двух случаев:

• Для $x \geq 0$, функция $y = 4x$. Решаем относительно $x$:

  $$x = \frac{y}{4}, \quad \text{так что} \quad y = \frac{x}{4}.$$

• Для $x < 0$, функция $y = 2x$. Решаем относительно $x$:

  $$x = \frac{y}{2}, \quad \text{так что} \quad y = \frac{x}{2}.$$

Таким образом, обратная функция для исходной функции имеет вид:

$$y = \begin{cases} \frac{1}{4}x, & \text{если } x \geq 0 \\ \frac{1}{2}x, & \text{если } x < 0 \end{cases}.$$

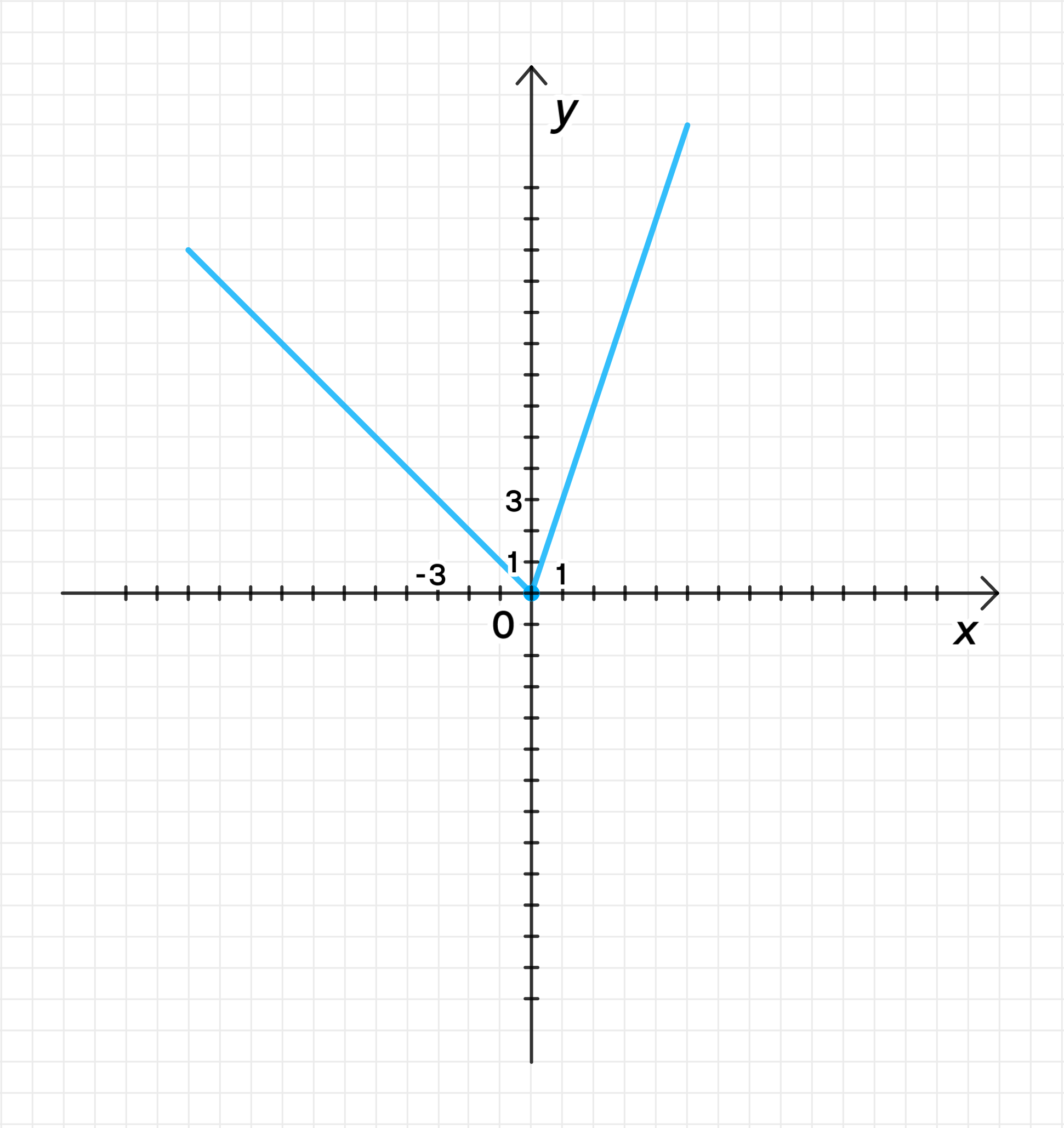
б) $y = x + 2|x|$

Разбиение на два случая:
Функция $y = x + 2|x|$ также зависит от знака $x$, и рассматриваем два случая:

• Если $x \geq 0$, то $|x| = x$, и функция будет:

  $$y = x + 2x = 3x.$$

• Если $x < 0$, то $|x| = -x$, и функция будет:

  $$y = x — 2x = -x.$$

Координаты некоторых точек:
Для некоторых значений $x$ получаем:

$$\begin{array}{c|c c c} x & -2 & 0 & 1 \\ \hline y & 2 & 0 & 3 \\ \end{array}$$

Для $x = -2$, $y = -(-2) = 2$.
Для $x = 0$, $y = 0$.
Для $x = 1$, $y = 3$.

График функции:
График функции будет состоять из двух прямых: одна с угловым коэффициентом 3 для $x \geq 0$, другая с угловым коэффициентом -1 для $x < 0$.

Обратная функция:
Мы видим, что для функции $y = 3x$ и $y = -x$ не существует взаимно обратных функций, так как при $x \geq 0$ и $x < 0$ функции не пересекаются и не могут быть инвертированы в едином виде.

Ответ: обратной функции не существует.

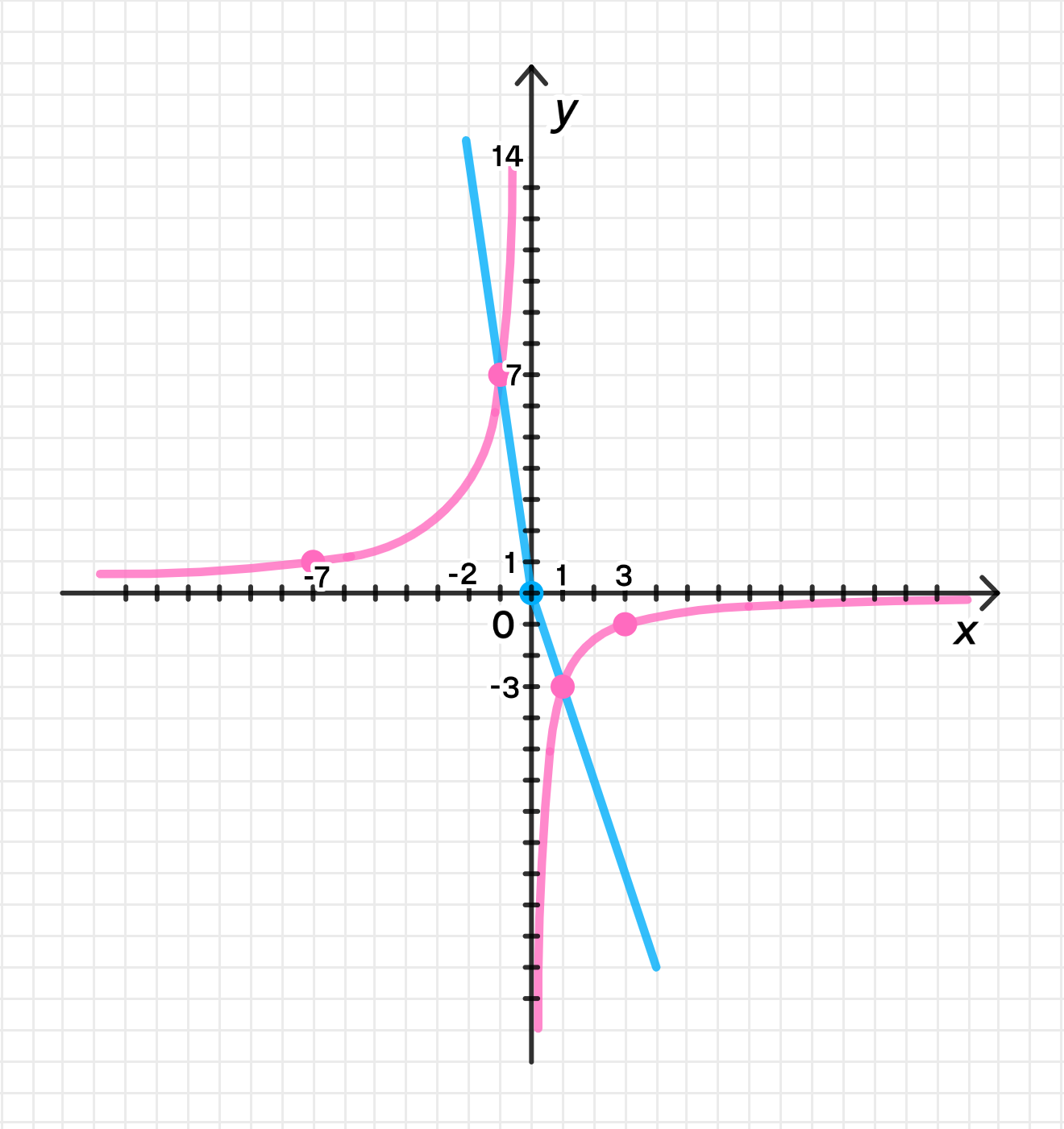
в) $y = 2|x| — 5x$

Разбиение на два случая:
Рассмотрим два случая для функции $y = 2|x| — 5x$:

• Если $x \geq 0$, то $|x| = x$, и функция будет:

  $$y = 2x — 5x = -3x.$$

• Если $x < 0$, то $|x| = -x$, и функция будет:

  $$y = -2x — 5x = -7x.$$

Координаты некоторых точек:
Для некоторых значений $x$ получаем:

$$\begin{array}{c|c c c} x & -1 & 0 & 1 \\ \hline y & 7 & 0 & -3 \\ \end{array}$$

Для $x = -1$, $y = -7(-1) = 7$.
Для $x = 0$, $y = 0$.
Для $x = 1$, $y = -3(1) = -3$.

График функции:
График функции состоит из двух прямых: одна с угловым коэффициентом -3 для $x \geq 0$, другая с угловым коэффициентом -7 для $x < 0$.

Обратная функция:
Теперь найдем обратную функцию для каждого из двух случаев:

• Для $x \geq 0$, $y = -3x$, решим относительно $x$:

  $$x = -\frac{y}{3}, \quad \text{так что} \quad y = -\frac{x}{3}.$$

• Для $x < 0$, $y = -7x$, решим относительно $x$:

  $$x = -\frac{y}{7}, \quad \text{так что} \quad y = -\frac{x}{7}.$$

Таким образом, обратная функция имеет вид:

$$y = \begin{cases} -\frac{1}{3}x, & \text{если } x < 0 \\ -\frac{1}{7}x, & \text{если } x \geq 0 \end{cases}.$$

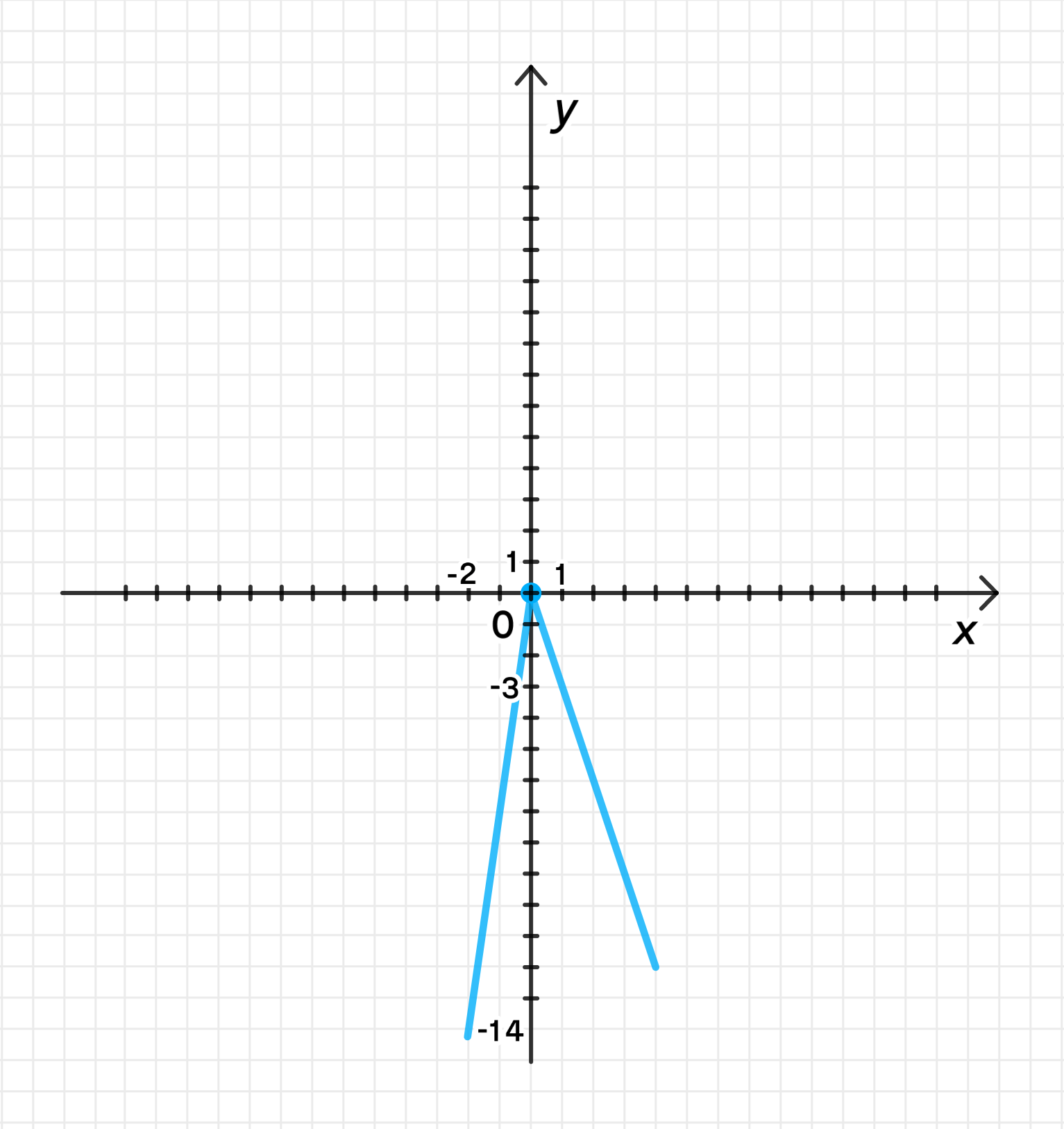
г) $y = 2x — 5|x|$

Разбиение на два случая:
Рассмотрим два случая для функции $y = 2x — 5|x|$:

• Если $x \geq 0$, то $|x| = x$, и функция будет:

  $$y = 2x — 5x = -3x.$$

• Если $x < 0$, то $|x| = -x$, и функция будет:

  $$y = 2x + 5x = 7x.$$

Координаты некоторых точек:
Для некоторых значений $x$ получаем:

$$\begin{array}{c|c c c} x & -1 & 0 & 1 \\ \hline y & -7 & 0 & -3 \\ \end{array}$$

Для $x = -1$, $y = 7(-1) = -7$.
Для $x = 0$, $y = 0$.
Для $x = 1$, $y = -3(1) = -3$.

График функции:
График функции состоит из двух прямых: одна с угловым коэффициентом -3 для $x \geq 0$, другая с угловым коэффициентом 7 для $x < 0$.

Обратная функция:
В данном случае не существует обратной функции, так как функция не является взаимно однозначной (не проходит горизонтальный тест на инъективность, поскольку одна и та же $y$-координата может быть достигнута для разных значений $x$).

Ответ: обратной функции не существует.