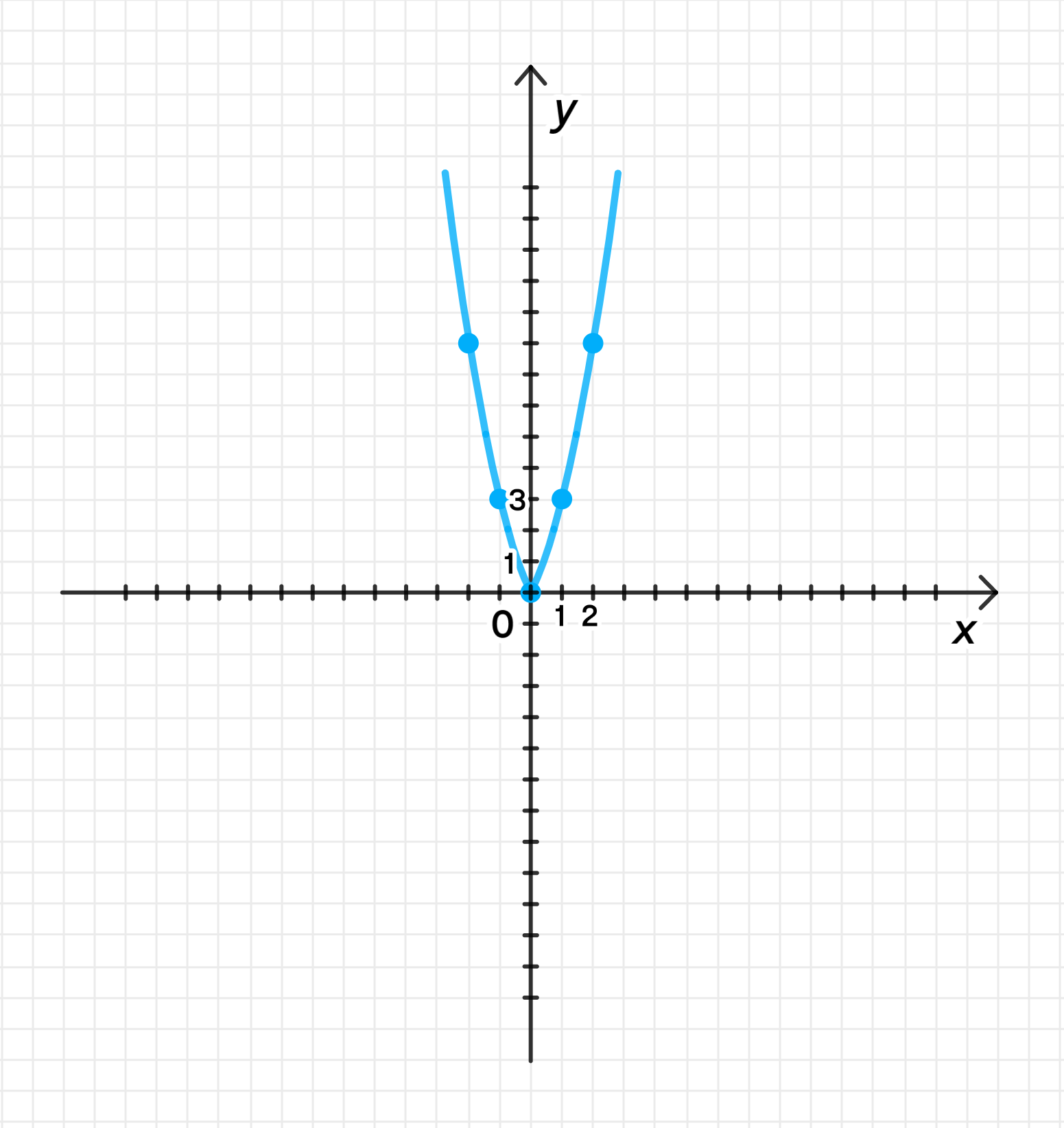ГДЗ по Алгебре 10 Класс Номер 10.35 Профильный Уровень Мордкович — Подробные Ответы

а) у = х|х|;

б) у = x² + 2|x|;

в) у = 2 — x|x|;

г) у = х|х — 2|.

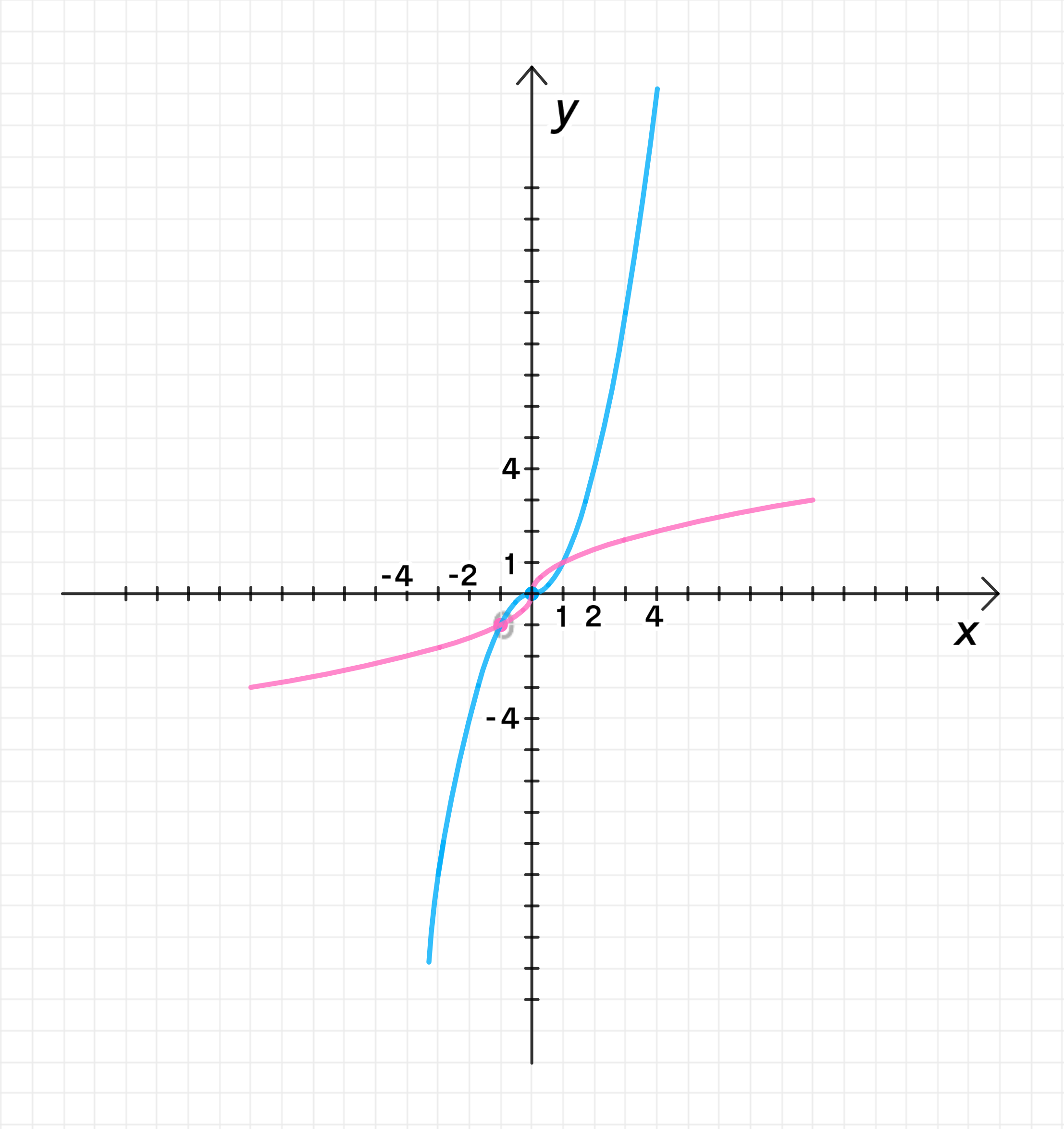
а) $y = x|x|$;

Если $x \geq 0$, тогда:

$$y = x \cdot x = x^2;$$

Если $x < 0$, тогда:

$$y = x \cdot (-x) = -x^2;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c c c} x & -2 & -1 & 0 & 1 & 2 \\ \hline y & -4 & -1 & 0 & 1 & 4 \\ \end{array}$$

График функции:

Обратная функция существует:

$$x = y^2 \implies y = \sqrt{x};$$ $$x = -y^2 \implies y^2 = -x \implies y = -\sqrt{-x};$$

Ответ:

$$y = \begin{cases} \sqrt{x}, & \text{если } x \geq 0 \\ -\sqrt{-x}, & \text{если } x < 0 \end{cases}.$$

б) $y = x^2 + 2|x|$;

Если $x \geq 0$, тогда:

$$y = x^2 + 2x;$$ $$x_0 = -\frac{b}{2a} = -\frac{2}{2 \cdot 1} = -1;$$

Если $x < 0$, тогда:

$$y = x^2 — 2x;$$ $$x_0 = -\frac{b}{2a} = -\frac{-2}{2 \cdot 1} = 1;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c c c} x & -2 & -1 & 0 & 1 & 2 \\ \hline y & 8 & 3 & 0 & 3 & 8 \\ \end{array}$$

График функции:

Обратной функции не существует;

Ответ: нет.

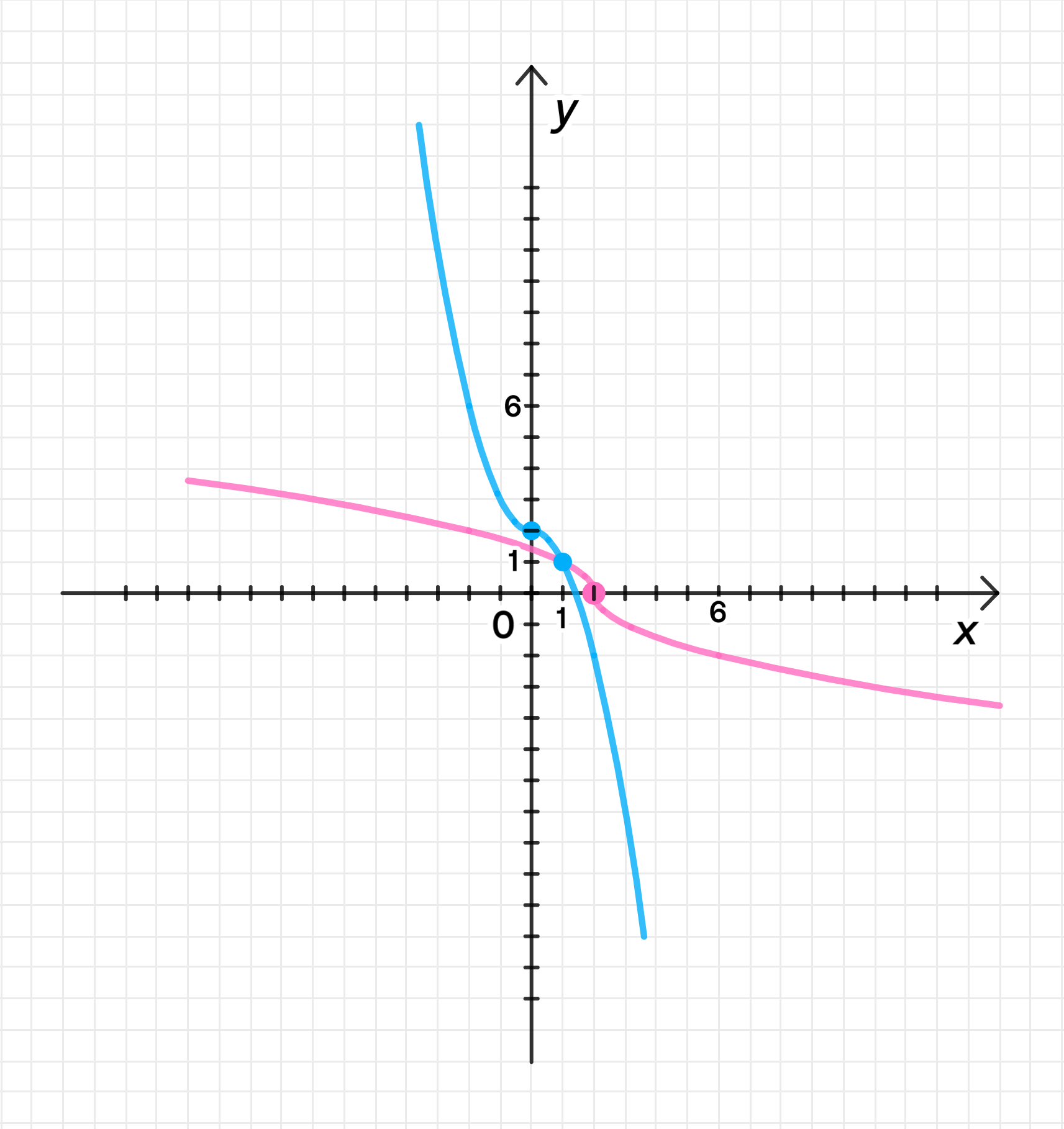
в) $y = 2 — x|x|$;

Если $x \geq 0$, тогда:

$$y = 2 — x \cdot x = 2 — x^2;$$

Если $x < 0$, тогда:

$$y = 2 — x \cdot (-x) = 2 + x^2;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c c c} x & -2 & -1 & 0 & 1 & 2 \\ \hline y & 6 & 3 & 2 & 1 & -2 \\ \end{array}$$

График функции:

Обратная функция существует:

$$x = 2 — y^2 \implies y^2 = 2 — x \implies y = \sqrt{2 — x};$$ $$x = 2 + y^2 \implies y^2 = x — 2 \implies y = -\sqrt{x — 2};$$

Ответ:

$$y = \begin{cases} \sqrt{2 — x}, & \text{если } x \leq 2 \\ -\sqrt{x — 2}, & \text{если } x > 2 \end{cases}.$$

г) $y = x|x — 2|$;

Если $x \geq 2$, тогда:

$$y = x(x — 2) = x^2 — 2x;$$ $$x_0 = -\frac{b}{2a} = -\frac{-2}{2 \cdot 1} = 1;$$

Если $x < 0$, тогда:

$$y = -x(x — 2) = -x^2 + 2x;$$ $$x_0 = -\frac{b}{2a} = -\frac{2}{2 \cdot (-1)} = 1;$$

Координаты некоторых точек:

$$\begin{array}{c|c c c c c} x & -1 & 0 & 1 & 2 & 3 \\ \hline y & -3 & 0 & 1 & 0 & 3 \\ \end{array}$$

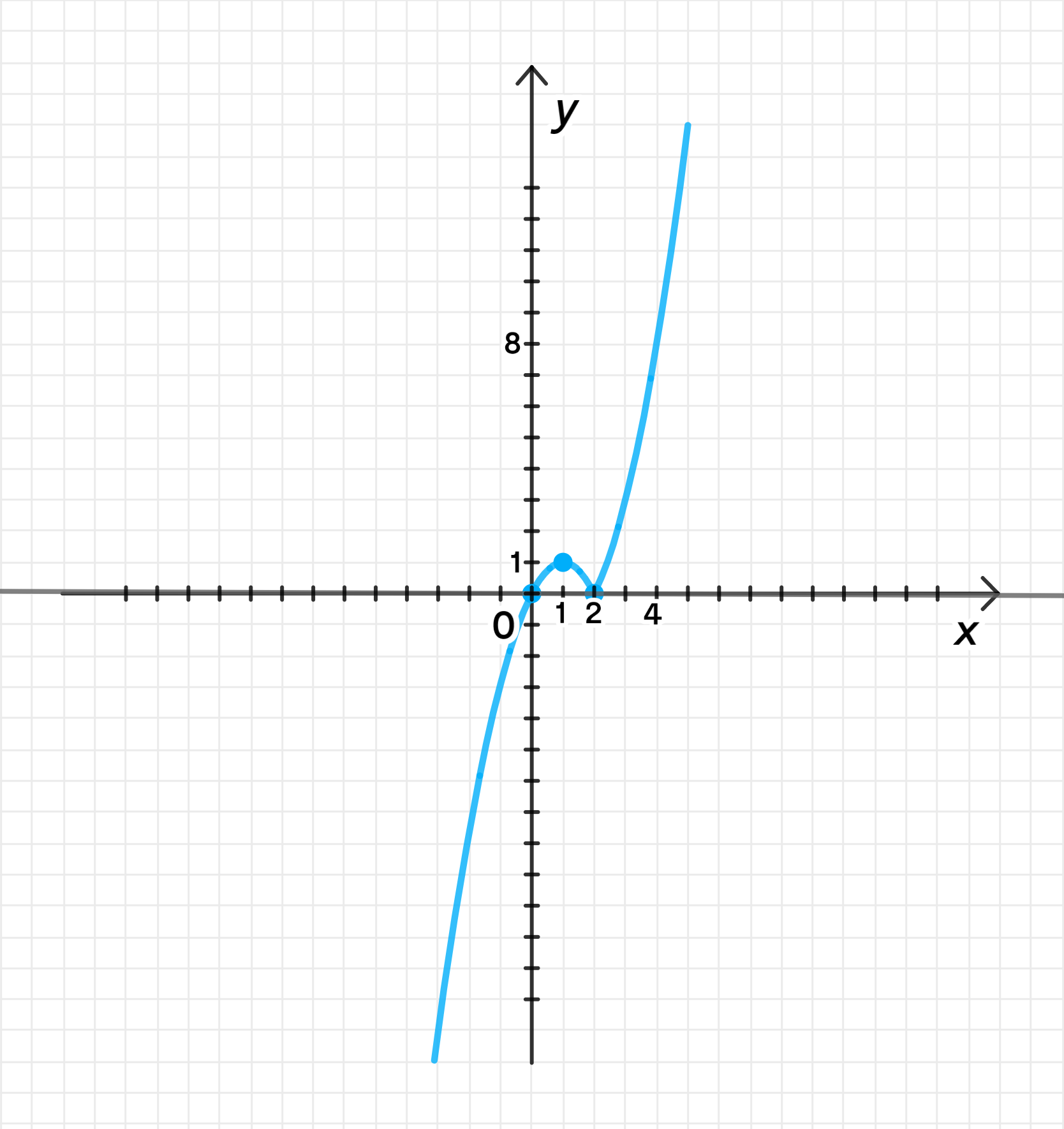
График функции:

Обратной функции не существует;

Ответ: нет.

$$\boxed{10.35}$$

а) $y = x|x|$

1. Разбиение на два случая

Функция $y = x|x|$ содержит абсолютную величину $|x|$, поэтому ее нужно рассматривать в двух случаях:

• Если $x \geq 0$, то $|x| = x$, и функция примет вид:

  $$y = x \cdot x = x^2.$$

  Это обычная квадратичная функция с параболой, открывающейся вверх.

• Если $x < 0$, то $|x| = -x$, и функция примет вид:

  $$y = x \cdot (-x) = -x^2.$$

  В этом случае график также является параболой, но она будет открываться вниз.

2. Координаты некоторых точек

Для того чтобы визуализировать поведение функции, выберем несколько значений $x$ и вычислим соответствующие $y$-координаты:

$$\begin{array}{c|c c c c c} x & -2 & -1 & 0 & 1 & 2 \\ \hline y & -4 & -1 & 0 & 1 & 4 \\ \end{array}$$

• Для $x = -2$: $y = (-2) \cdot |(-2)| = -4$.
• Для $x = -1$: $y = (-1) \cdot |(-1)| = -1$.
• Для $x = 0$: $y = 0 \cdot |0| = 0$.
• Для $x = 1$: $y = 1 \cdot |1| = 1$.
• Для $x = 2$: $y = 2 \cdot |2| = 4$.

3. График функции

График функции будет представлять собой две параболы:

• Для $x \geq 0$ — парабола $y = x^2$, открывающаяся вверх.
• Для $x < 0$ — парабола $y = -x^2$, открывающаяся вниз.
  Эти параболы соединяются в точке $x = 0$, где $y = 0$.

4. Обратная функция

Теперь определим обратную функцию для каждого из двух случаев:

• Для $x \geq 0$, функция $y = x^2$. Решаем относительно $x$:

  $$x = \sqrt{y} \quad \text{(так как \(x \geq 0\))}.$$

• Для $x < 0$, функция $y = -x^2$. Решаем относительно $x$:

  $$x = -\sqrt{-y} \quad \text{(так как \(x < 0\))}.$$

Таким образом, обратная функция для $y = x|x|$ будет:

$$y = \begin{cases} \sqrt{x}, & \text{если } x \geq 0 \\ -\sqrt{-x}, & \text{если } x < 0 \end{cases}.$$

б) $y = x^2 + 2|x|$

1. Разбиение на два случая

Функция $y = x^2 + 2|x|$ также содержит абсолютную величину, и для ее анализа нужно рассмотреть два случая:

• Если $x \geq 0$, то $|x| = x$, и функция примет вид:

  $$y = x^2 + 2x.$$

  Это стандартная квадратичная функция с линейным слагаемым.

• Если $x < 0$, то $|x| = -x$, и функция примет вид:

  $$y = x^2 — 2x.$$

  Это также квадратичная функция, но с другим линейным слагаемым.

2. Нахождение координаты вершины

Для каждой из этих функций находим координаты вершины. Вершина квадратичной функции $y = ax^2 + bx + c$ находится по формуле:

$$x_0 = -\frac{b}{2a}.$$

• Для $x \geq 0$, функция $y = x^2 + 2x$. Здесь $a = 1$, $b = 2$, поэтому:

  $$x_0 = -\frac{2}{2 \cdot 1} = -1.$$

• Для $x < 0$, функция $y = x^2 — 2x$. Здесь $a = 1$, $b = -2$, поэтому:

  $$x_0 = -\frac{-2}{2 \cdot 1} = 1.$$

3. Координаты некоторых точек

Вычислим несколько значений функции для разных $x$:

$$\begin{array}{c|c c c c c} x & -2 & -1 & 0 & 1 & 2 \\ \hline y & 8 & 3 & 0 & 3 & 8 \\ \end{array}$$

• Для $x = -2$: $y = (-2)^2 + 2(-2) = 8$.
• Для $x = -1$: $y = (-1)^2 + 2(-1) = 3$.
• Для $x = 0$: $y = 0^2 + 2(0) = 0$.
• Для $x = 1$: $y = 1^2 + 2(1) = 3$.
• Для $x = 2$: $y = 2^2 + 2(2) = 8$.

4. График функции

График функции будет представлять собой две параболы, одна с вершиной $x = -1$ для $x \geq 0$, и другая с вершиной $x = 1$ для $x < 0$. Обе параболы будут симметричны относительно вертикальной прямой.

5. Обратная функция

Для данной функции обратная функция не существует, поскольку она не является взаимно однозначной (она не инъективна). Это связано с тем, что для одного значения $y$ существует два значения $x$ (например, для $y = 3$, мы имеем $x = -1$ и $x = 1$).

Ответ: обратной функции не существует.

в) $y = 2 — x|x|$

1. Разбиение на два случая

Функция $y = 2 — x|x|$ также зависит от абсолютной величины $|x|$:

• Если $x \geq 0$, то $|x| = x$, и функция примет вид:

  $$y = 2 — x^2.$$

  Это парабола, направленная вниз.

• Если $x < 0$, то $|x| = -x$, и функция примет вид:

  $$y = 2 + x^2.$$

  Это парабола, направленная вверх.

2. Координаты некоторых точек

Вычислим несколько значений функции для различных $x$:

$$\begin{array}{c|c c c c c} x & -2 & -1 & 0 & 1 & 2 \\ \hline y & 6 & 3 & 2 & 1 & -2 \\ \end{array}$$

• Для $x = -2$: $y = 2 + (-2)^2 = 6$.
• Для $x = -1$: $y = 2 + (-1)^2 = 3$.
• Для $x = 0$: $y = 2 + 0^2 = 2$.
• Для $x = 1$: $y = 2 — 1^2 = 1$.
• Для $x = 2$: $y = 2 — 2^2 = -2$.

3. График функции

График будет состоять из двух парабол: одна с вершиной в точке $y = 2$ для $x = 0$ и направлена вниз для $x \geq 0$, а другая — с вершиной в точке $y = 2$ для $x = 0$ и направлена вверх для $x < 0$.

4. Обратная функция

Теперь найдем обратную функцию для каждого случая:

• Для $x \geq 0$, $y = 2 — x^2$, решаем относительно $x$:

  $$x^2 = 2 — y \quad \Rightarrow \quad x = \sqrt{2 — y}.$$

• Для $x < 0$, $y = 2 + x^2$, решаем относительно $x$:

  $$x^2 = y — 2 \quad \Rightarrow \quad x = -\sqrt{y — 2}.$$

Таким образом, обратная функция будет:

$$y = \begin{cases} \sqrt{2 — x}, & \text{если } x \leq 2 \\ -\sqrt{x — 2}, & \text{если } x > 2 \end{cases}.$$

г) $y = x|x — 2|$

1. Разбиение на два случая

Функция $y = x|x — 2|$ также зависит от знака выражения $x — 2$:

• Если $x \geq 2$, то $|x — 2| = x — 2$, и функция примет вид:

  $$y = x(x — 2) = x^2 — 2x.$$

• Если $x < 2$, то $|x — 2| = 2 — x$, и функция примет вид:

  $$y = x(2 — x) = -x^2 + 2x.$$

2. Координаты некоторых точек

Вычислим несколько значений функции:

$$\begin{array}{c|c c c c c} x & -1 & 0 & 1 & 2 & 3 \\ \hline y & -3 & 0 & 1 & 0 & 3 \\ \end{array}$$

• Для $x = -1$, $y = (-1)(2 — (-1)) = -3$.
• Для $x = 0$, $y = 0(2 — 0) = 0$.
• Для $x = 1$, $y = 1(2 — 1) = 1$.
• Для $x = 2$, $y = 2(2 — 2) = 0$.
• Для $x = 3$, $y = 3(3 — 2) = 3$.

3. График функции

График будет состоять из двух парабол:

• Для $x \geq 2$ — парабола $y = x^2 — 2x$, открывающаяся вверх.
• Для $x < 2$ — парабола $y = -x^2 + 2x$, открывающаяся вниз.

4. Обратная функция

Обратной функции не существует, так как функция не является инъективной (она не проходит горизонтальный тест на инъективность). Одно и то же значение $y$ может быть получено для разных значений $x$.

Ответ: обратной функции не существует.