Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 10.4 Профильный Уровень Мордкович — Подробные Ответы
Для функции, заданной табличным способом, укажите ее область определения и выясните, имеет эта функция в своей области определения обратную функцию или нет; в случае положительного ответа постройте график обратной функции:
Функция обратима на множестве , если любое свое значение она принимает только в одной точке на .
а) Таблица значений функции:
| 1 | 2 | 5 | 7 | |
|---|---|---|---|---|
| 3 | 4 | 7 | 3 |
Область определения функции: ;
При и , функция принимает одно и то же значение , следовательно, она не является обратимой;
График функции:
б) Таблица значений функции:
| 5 | 7 | |||
|---|---|---|---|---|
| 0,(6) | 1,(4) |
и ;
Область определения функции: ;
При и , функция принимает одно и то же значение , следовательно, она не является обратимой;
График функции:
в) Таблица значений функции:
| 1 | 2 | 3 | 7 | |
|---|---|---|---|---|
| 5 | 8 | 9 | 1 |
Область определения функции: ;
Каждое свое значение функция принимает только при одном значении , следовательно, она является обратимой;
Таблица значений обратной функции:
| 5 | 8 | 9 | 1 | |
|---|---|---|---|---|
| 1 | 2 | 3 | 7 |
График обратной функции:
г) Таблица значений функции:
| -1 | 1 | 2 | 5 | |
|---|---|---|---|---|
| 4 | 1,(7) | 1 |
;
Область определения функции: ;
Каждое свое значение функция принимает только при одном значении , следовательно, она является обратимой;
Таблица значений обратной функции:
| 4 | 1 | |||
|---|---|---|---|---|
| -1 | 1 | 2 | 5 |
График обратной функции:
Функция называется обратимой на множестве , если для каждого значения из её области значений существует только одно значение из области определения, такое что . Это означает, что функция должна быть инъективной (или взаимно однозначной), то есть каждое значение функции должно быть получено при помощи ровно одного значения . Таким образом, для того чтобы функция была обратимой, её область определения не должна содержать двух одинаковых значений функции для разных значений .
а) Таблица значений функции:
| 1 | 2 | 5 | 7 | |
|---|---|---|---|---|
| 3 | 4 | 7 | 3 |
1) Область определения функции:
Область определения функции – это множество всех возможных значений , для которых определена функция . В данном случае функция определена на множестве . Следовательно, область определения функции:
2) Анализ на обратимость:
Чтобы функция была обратимой, она должна быть инъективной, то есть каждое значение функции должно быть получено при помощи ровно одного значения .
Из таблицы значений видно, что при и , функция принимает одно и то же значение . Это означает, что два различных значения (1 и 7) дают одно и то же значение функции, что нарушает инъективность функции. Следовательно, функция не является обратимой.
б) Таблица значений функции:
| 5 | 7 | |||
|---|---|---|---|---|
| 0,(6) | 1,(4) |
1) Область определения функции:
Область определения функции — это множество всех значений , для которых функция имеет значения . В данной таблице принимает значения . Следовательно, область определения функции:
2) Анализ на обратимость:
Функция будет обратимой, если для каждого значения существует только одно значение , при котором .
Из таблицы значений видно, что при и , функция принимает одно и то же значение . Это означает, что два различных значения ( и ) дают одно и то же значение , что нарушает инъективность функции. Следовательно, функция не является обратимой.
в) Таблица значений функции:
| 1 | 2 | 3 | 7 | |
|---|---|---|---|---|
| 5 | 8 | 9 | 1 |
1) Область определения функции:
Область определения функции состоит из всех значений , для которых функция принимает определённые значения. Из таблицы значений видно, что функция определена на множестве . Следовательно, область определения функции:
2) Анализ на обратимость:
Функция будет обратимой, если для каждого значения существует только одно значение , при котором .
Из таблицы видно, что каждому значению соответствует только одно значение . Например:
- при ,
- при ,
- при ,
- при .
Каждое значение получается при единственном значении . Следовательно, функция обратима.
3) Таблица значений обратной функции:
Обратная функция для каждого значения будет возвращать соответствующее значение . Таким образом, таблица значений обратной функции будет выглядеть так:
| 5 | 8 | 9 | 1 | |
|---|---|---|---|---|
| 1 | 2 | 3 | 7 |
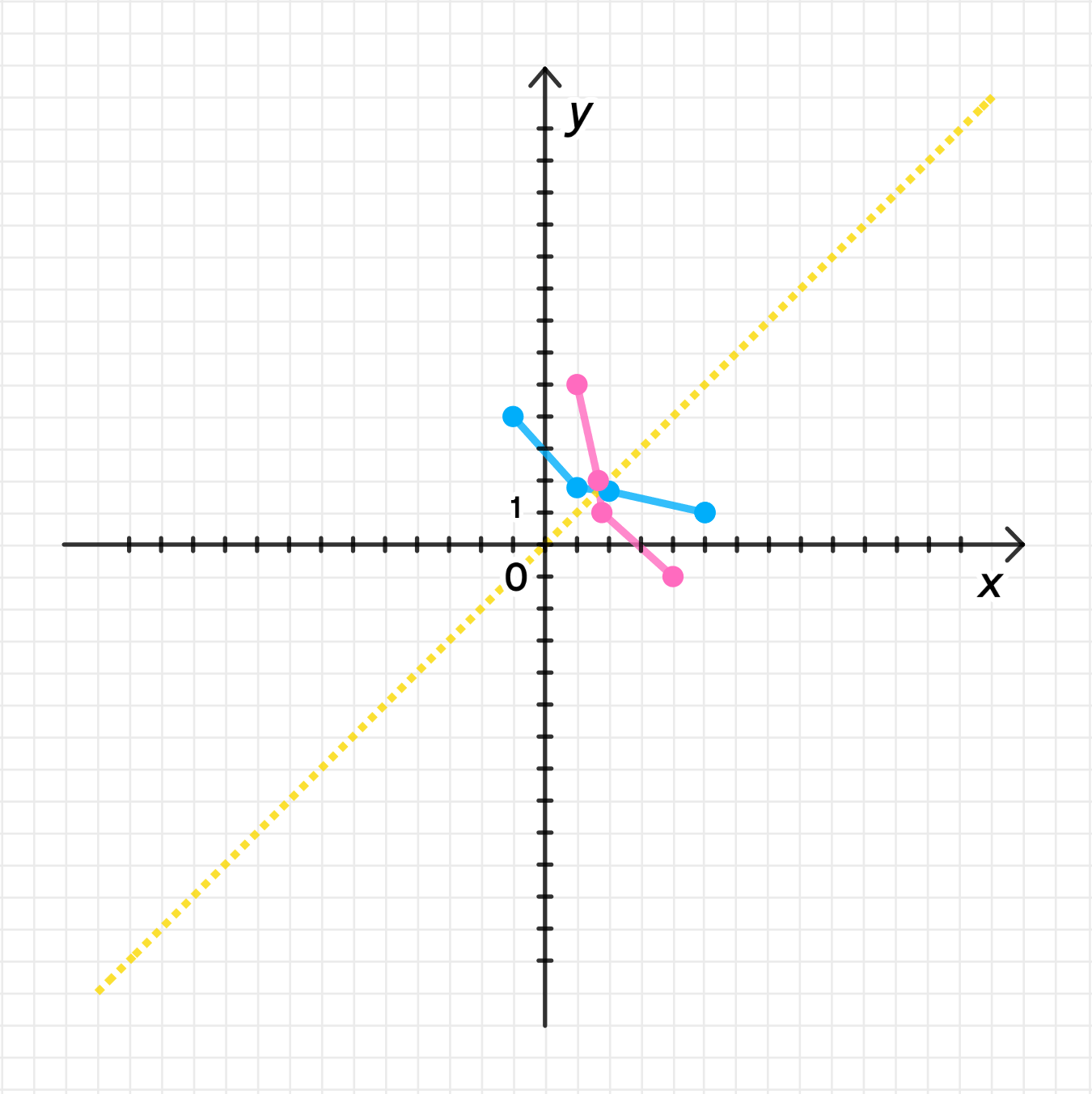
4) График обратной функции:
График обратной функции будет получен путём отражения графика исходной функции относительно прямой . (График представлен на рисунке).
г) Таблица значений функции:
| -1 | 1 | 2 | 5 | |
|---|---|---|---|---|
| 4 | 1,(7) | 1 |
1) Область определения функции:
Область определения функции — это множество всех значений , для которых определена функция. В данной таблице функция определена на множестве . Следовательно, область определения функции:
2) Анализ на обратимость:
Функция будет обратимой, если для каждого значения существует только одно значение , при котором .
Из таблицы значений видно, что каждому значению соответствует только одно значение :
- при ,
- при ,
- при ,
- при .
Каждое значение получается при единственном значении . Следовательно, функция обратима.
3) Таблица значений обратной функции:
Обратная функция для каждого значения будет возвращать соответствующее значение . Таким образом, таблица значений обратной функции будет выглядеть так:
| 4 | 1 | |||
|---|---|---|---|---|
| -1 | 1 | 2 | 5 |
4) График обратной функции:
График обратной функции будет также получен путём отражения графика исходной функции относительно прямой . (График представлен на рисунке).
Заключение:
- В примере а) и б) функции не являются обратимыми, так как при разных значениях принимаются одинаковые значения , что нарушает инъективность функции.
- В примерах в) и г) функции являются обратимыми, так как каждое значение принимается только при одном значении , что подтверждает инъективность этих функций.
Таким образом, для обратимости функции важно, чтобы на множестве каждое значение имело только одно соответствующее ему значение .