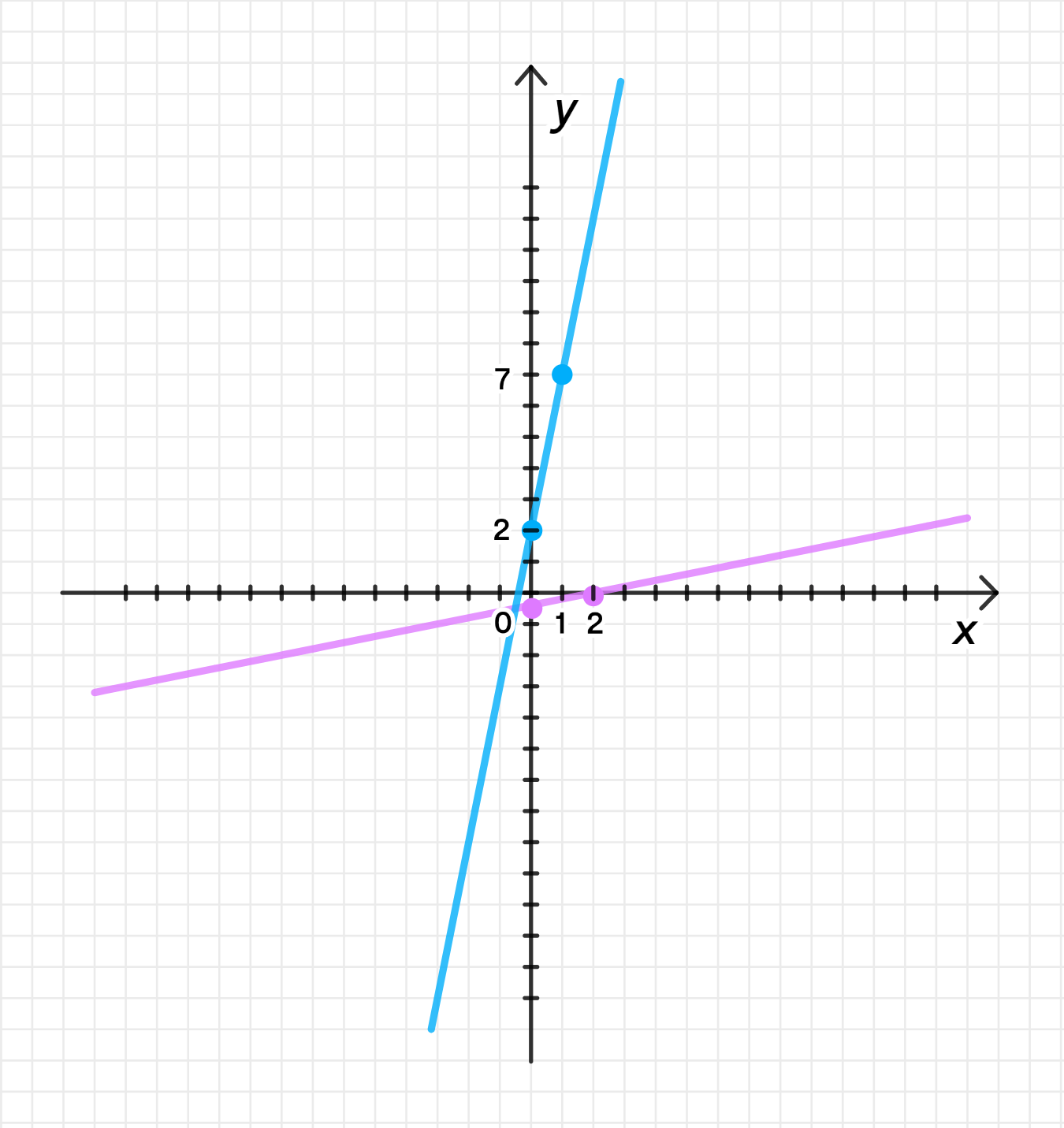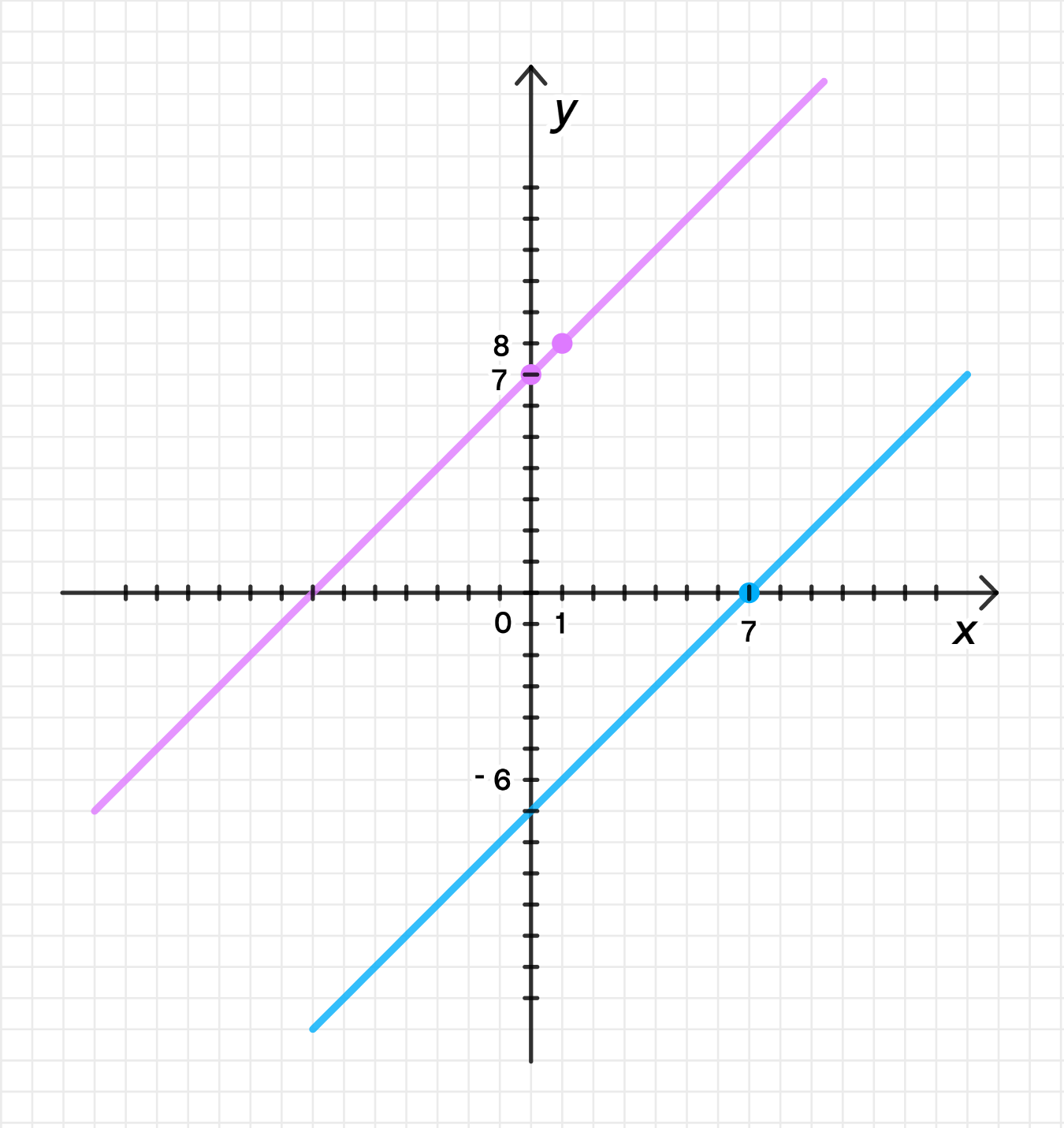ГДЗ по Алгебре 10 Класс Номер 10.8 Профильный Уровень Мордкович — Подробные Ответы

Найдите функцию, обратную данной. Постройте на одном чертеже графики этих взаимно-обратных функций:

а) у = 3х;

б) y = 5х + 2;

в) у = х — 7;

г) у = $\frac{1}{3}x$ — 4.

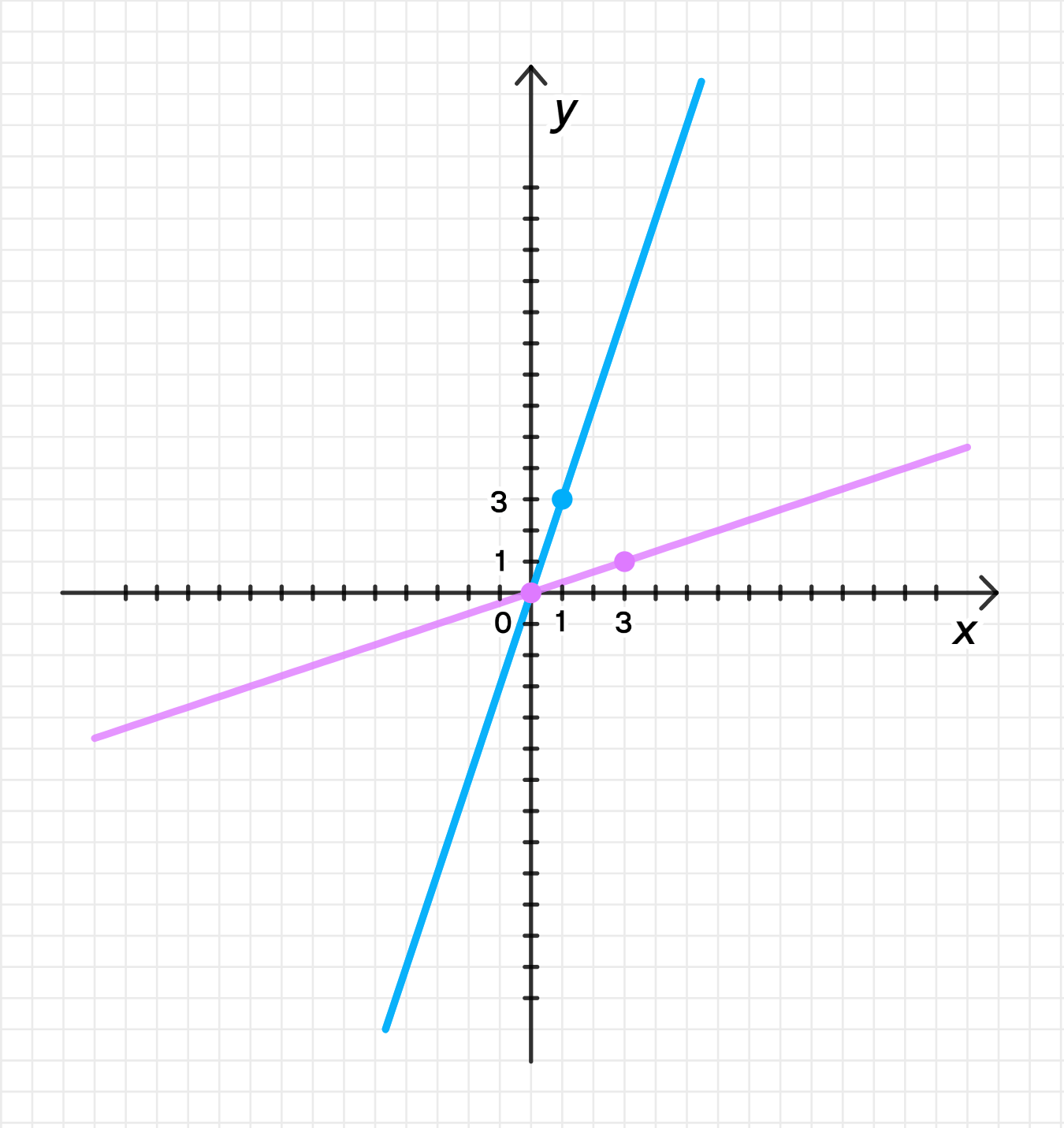
а) $y = 3x$

Функция, обратная данной:

$$x = 3y;$$ $$y = \frac{x}{3};$$

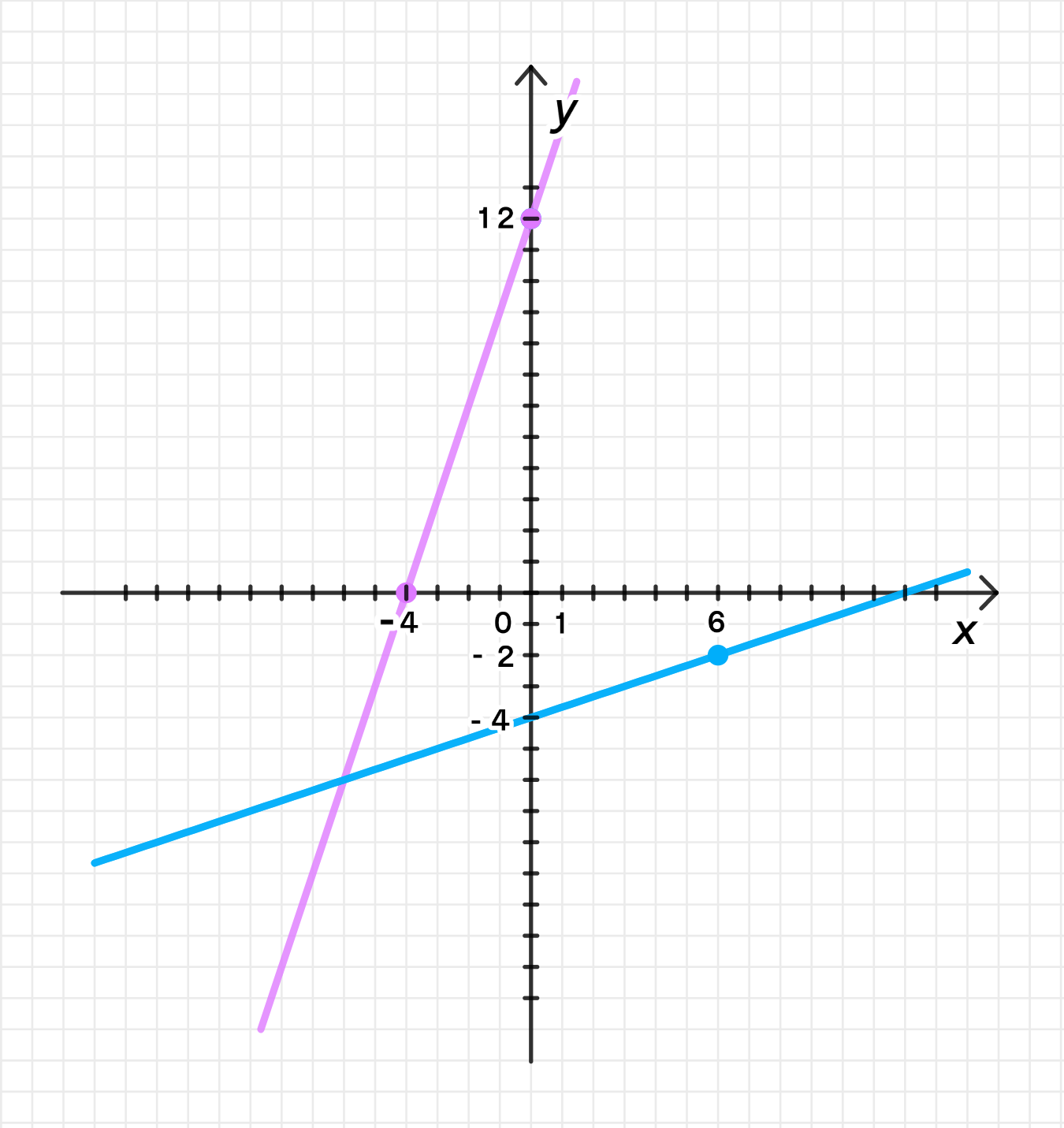
Графики функций:

Ответ: $y = \frac{x}{3}$.

б) $y = 5x + 2$

Функция, обратная данной:

$$x = 5y + 2;$$ $$5y = x — 2;$$ $$y = \frac{x — 2}{5};$$

Графики функций:

Ответ: $y = \frac{x — 2}{5}$.

в) $y = x — 7$

Функция, обратная данной:

$$x = y — 7;$$ $$y = x + 7;$$

Графики функций:

Ответ: $y = x + 7$.

г) $y = \frac{1}{3}x — 4$

Функция, обратная данной:

$$x = \frac{1}{3}y — 4;$$ $$\frac{1}{3}y = x + 4;$$ $$y = 3(x + 4);$$ $$y = 3x + 12;$$

Графики функций:

Ответ: $y = 3x + 12$.

а) $y = 3x$

Нахождение обратной функции:

Для того чтобы найти обратную функцию, нужно выразить $x$ через $y$. Начнем с исходной функции:

$$y = 3x$$

Для нахождения обратной функции:

$$x = \frac{y}{3}$$

Теперь выразим $y$ через $x$:

$$y = \frac{x}{3}$$

Это и есть обратная функция. Ответ:

$$y = \frac{x}{3}$$

Таблица значений:

Теперь, чтобы определить точности, подставим конкретные значения для $x$ и вычислим соответствующие значения $y$ по обеим функциям.

Для функции $y = 3x$ при $x = 0$ получаем $y = 3(0) = 0$.

Для функции $y = 3x$ при $x = 3$ получаем $y = 3(3) = 9$.

Теперь вычислим значения для обратной функции $y = \frac{x}{3}$:

Для функции $y = \frac{x}{3}$ при $x = 0$ получаем $y = \frac{0}{3} = 0$.

Для функции $y = \frac{x}{3}$ при $x = 3$ получаем $y = \frac{3}{3} = 1$.

Таким образом, для обратной функции и функции получаем:

График функции:

График функции $y = 3x$ — это прямая, проходящая через начало координат, с угловым коэффициентом 3.

График обратной функции $y = \frac{x}{3}$ — это прямая с угловым коэффициентом $\frac{1}{3}$, также проходящая через начало координат.

Ответ: $y = \frac{x}{3}$.

б) $y = 5x + 2$

Нахождение обратной функции:

Начнем с исходной функции:

$$y = 5x + 2$$

Чтобы выразить $x$ через $y$, сначала изолируем $x$:

$$y — 2 = 5x$$

Делим обе части на 5:

$$x = \frac{y — 2}{5}$$

Теперь выразим $y$ через $x$:

$$y = \frac{x — 2}{5}$$

Это и есть обратная функция. Ответ:

$$y = \frac{x — 2}{5}$$

Таблица значений:

Для функции $y = 5x + 2$ подставим следующие значения для $x$:

При $x = -3$, $y = 5(-3) + 2 = -15 + 2 = -13$.

При $x = 2$, $y = 5(2) + 2 = 10 + 2 = 12$.

Для обратной функции $y = \frac{x — 2}{5}$:

При $x = -3$, $y = \frac{-3 — 2}{5} = \frac{-5}{5} = -1$.

При $x = 2$, $y = \frac{2 — 2}{5} = \frac{0}{5} = 0$.

Итак, значения для таблицы:

График функции:

График функции $y = 5x + 2$ — это прямая с угловым коэффициентом 5, пересекающая ось $y$ в точке 2.

График обратной функции $y = \frac{x — 2}{5}$ — это прямая с угловым коэффициентом $\frac{1}{5}$, пересекающая ось $y$ в точке -2.

Ответ: $y = \frac{x — 2}{5}$.

в) $y = x — 7$

Нахождение обратной функции:

Начнем с исходной функции:

$$y = x — 7$$

Чтобы выразить $x$ через $y$, изолируем $x$:

$$x = y + 7$$

Теперь выразим $y$ через $x$:

$$y = x + 7$$

Это и есть обратная функция. Ответ:

$$y = x + 7$$

Таблица значений:

Для функции $y = x — 7$:

При $x = -6$, $y = -6 — 7 = -13$.

При $x = -1$, $y = -1 — 7 = -8$.

Для обратной функции $y = x + 7$:

При $x = -6$, $y = -6 + 7 = 1$.

При $x = -1$, $y = -1 + 7 = 6$.

Таблица значений для обратной функции и функции:

График функции:

График функции $y = x — 7$ — это прямая с угловым коэффициентом 1, пересекающая ось $y$ в точке -7.

График обратной функции $y = x + 7$ — это прямая с угловым коэффициентом 1, пересекающая ось $y$ в точке 7.

Ответ: $y = x + 7$.

г) $y = \frac{1}{3}x — 4$

Нахождение обратной функции:

Начнем с исходной функции:

$$y = \frac{1}{3}x — 4$$

Чтобы выразить $x$ через $y$, изолируем $x$:

$$y + 4 = \frac{1}{3}x$$

Умножим обе части на 3:

$$3(y + 4) = x$$

Таким образом, получаем:

$$x = 3(y + 4)$$

Теперь выразим $y$ через $x$:

$$y = 3(x + 4)$$

Это и есть обратная функция. Ответ:

$$y = 3(x + 4)$$

Таблица значений:

Для функции $y = \frac{1}{3}x — 4$:

При $x = -4$, $y = \frac{1}{3}(-4) — 4 = -\frac{4}{3} — 4 = -\frac{16}{3}$.

При $x = -3$, $y = \frac{1}{3}(-3) — 4 = -1 — 4 = -5$.

Для обратной функции $y = 3(x + 4)$:

При $x = -4$, $y = 3(-4 + 4) = 3(0) = 0$.

При $x = -3$, $y = 3(-3 + 4) = 3(1) = 3$.

Таблица значений для функции и обратной функции:

График функции:

График функции $y = \frac{1}{3}x — 4$ — это прямая с угловым коэффициентом $\frac{1}{3}$, пересекающая ось $y$ в точке -4.

График обратной функции $y = 3(x + 4)$ — это прямая с угловым коэффициентом 3, пересекающая ось $y$ в точке 12.

Ответ: $y = 3(x + 4)$.