ГДЗ по Алгебре 10 Класс Номер 102 Повторение Профильный Уровень Мордкович — Подробные Ответы

Решите графически уравнение:

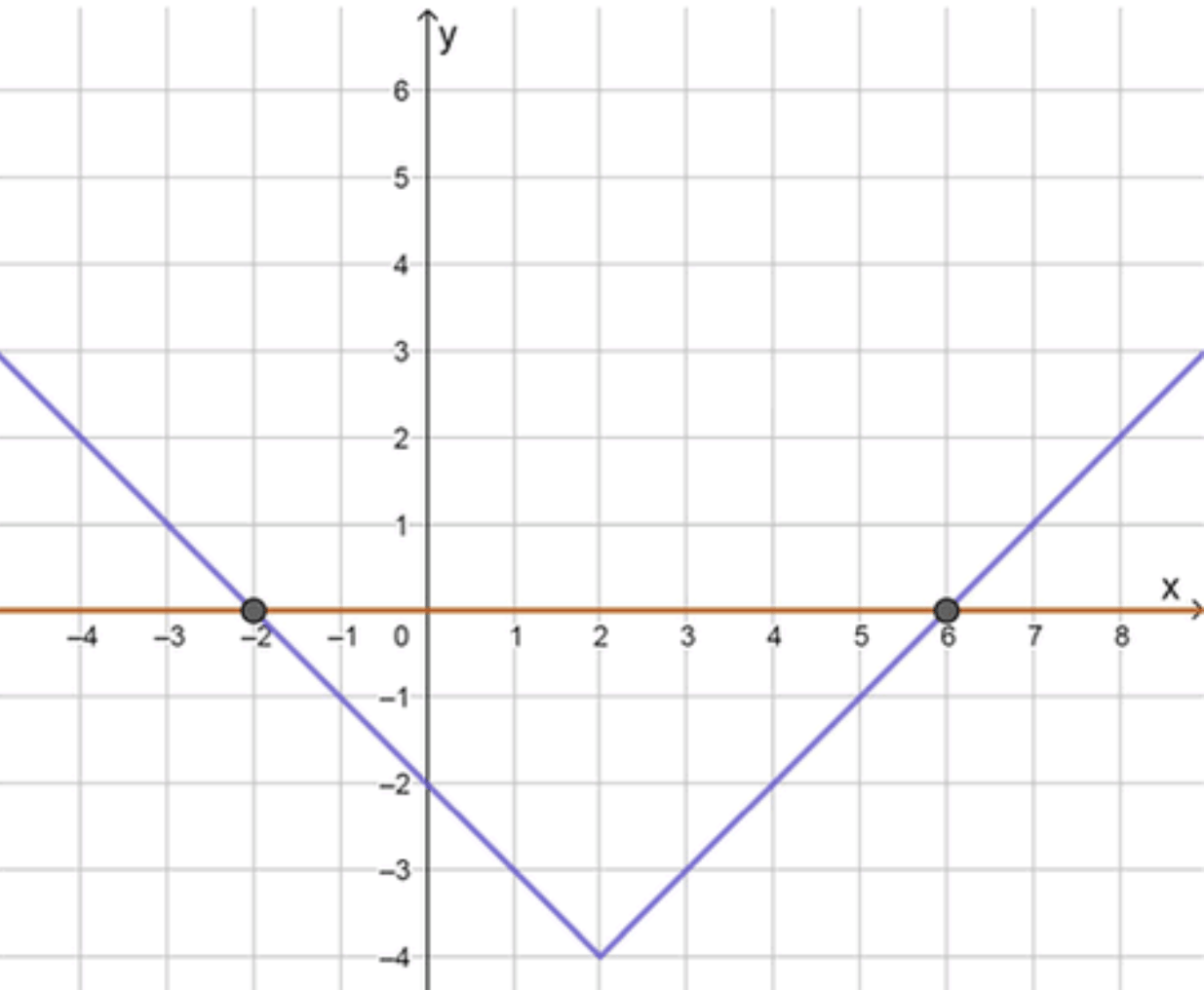
а) |х — 2| — 4 = 0;

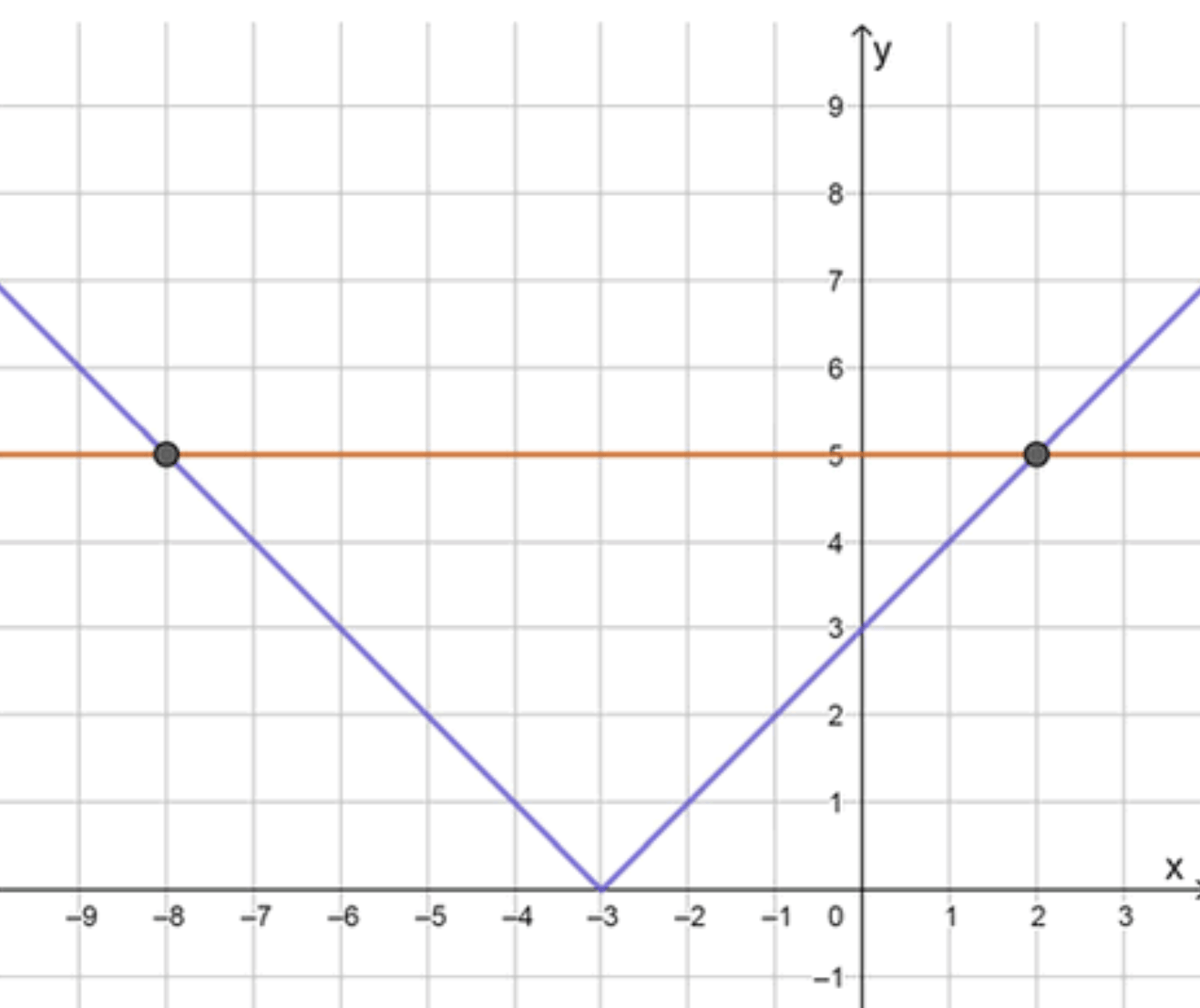
б)|х + 3| = 5;

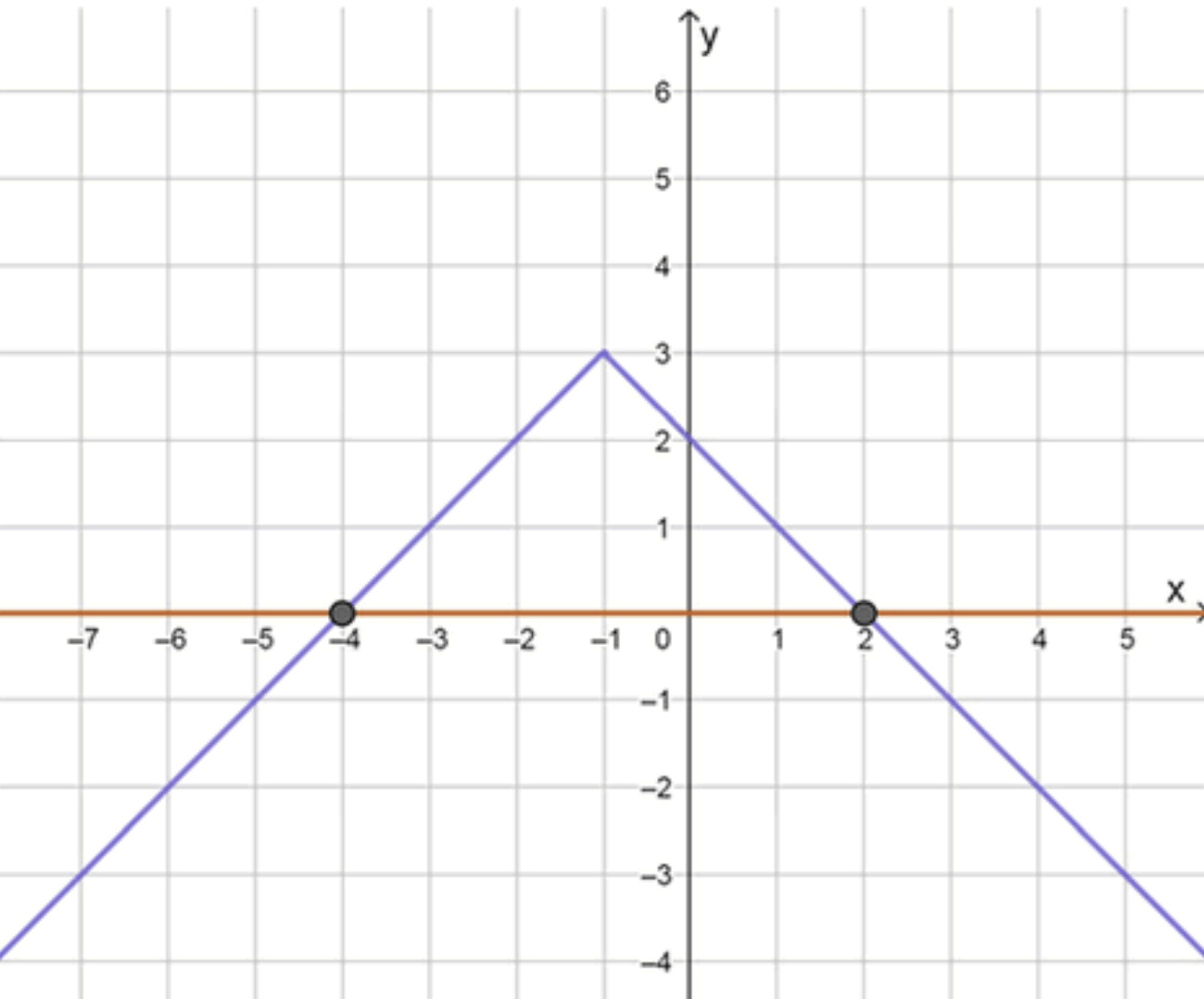
в) 3 — |х + 1| = 0;

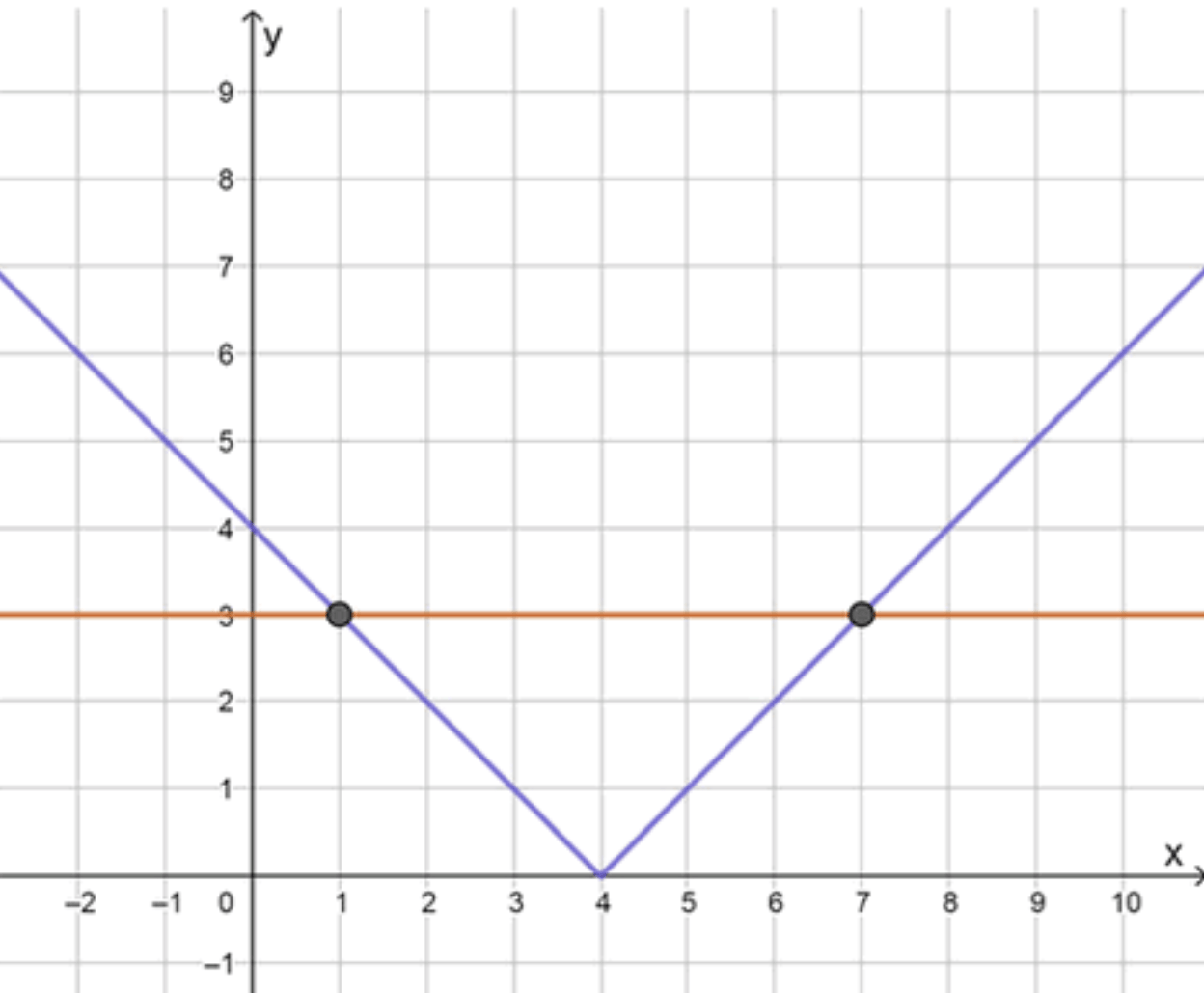
г)|x-4|= 3.

а) $|x — 2| — 4 = 0$;

$y = |x — 2| — 4$ — график модуля:
$x_0 = 2$ и $y_0 = -4$;

$y = 0$ — уравнение прямой;

Графики функций:

Ответ: $x_1 = -2$, $x_2 = 6$.

б) $|x + 3| = 5$;

$y = |x + 3| — 5$ — график модуля:
$x_0 = -3$ и $y_0 = 0$;

$y = 5$ — уравнение прямой;

Графики функций:

Ответ: $x_1 = -8$, $x_2 = 2$.

в) $3 — |x + 1| = 0$;

$y = 3 — |x + 1|$ — график модуля:
$x_0 = -1$ и $y_0 = 3$;

$y = 0$ — уравнение прямой;

Графики функций:

Ответ: $x_1 = -4$, $x_2 = 2$.

г) $|x — 4| = 3$;

$y = |x — 4| — 3$ — график модуля:
$x_0 = 4$ и $y_0 = 0$;

$y = 3$ — уравнение прямой;

Графики функций:

Ответ: $x_1 = 1$, $x_2 = 7$.

а) $|x — 2| — 4 = 0$

Перепишем уравнение:

$$|x — 2| — 4 = 0$$

Для того чтобы избавиться от минуса, добавим 4 с обеих сторон:

$$|x — 2| = 4$$

Рассмотрим два случая для модуля:

Модуль выражения $|x — 2|$ принимает два значения:

• $x — 2 = 4$ (положительное выражение внутри модуля),
• $x — 2 = -4$ (отрицательное выражение внутри модуля).

Решим оба случая:

• Для $x — 2 = 4$:

$$x = 4 + 2 = 6$$

• Для $x — 2 = -4$:

$$x = -4 + 2 = -2$$

Ответ:

Корни уравнения: $x_1 = -2$, $x_2 = 6$.

б) $|x + 3| = 5$

Перепишем уравнение:

$$|x + 3| = 5$$

Мы имеем модуль, который равен 5. Модуль принимает два значения:

• $x + 3 = 5$ (положительное выражение внутри модуля),
• $x + 3 = -5$ (отрицательное выражение внутри модуля).

Решим оба случая:

• Для $x + 3 = 5$:

  $$x = 5 — 3 = 2$$

• Для $x + 3 = -5$:

  $$x = -5 — 3 = -8$$

Ответ:

Корни уравнения: $x_1 = -8$, $x_2 = 2$.

в) $3 — |x + 1| = 0$

Перепишем уравнение:

$$3 — |x + 1| = 0$$

Чтобы избавиться от минуса, добавим $|x + 1|$ с обеих сторон:

$$3 = |x + 1|$$

Таким образом, модуль $|x + 1|$ равен 3.

Рассмотрим два случая для модуля:

• $x + 1 = 3$ (положительное выражение внутри модуля),
• $x + 1 = -3$ (отрицательное выражение внутри модуля).

Решим оба случая:

• Для $x + 1 = 3$:

  $$x = 3 — 1 = 2$$

• Для $x + 1 = -3$:

  $$x = -3 — 1 = -4$$

Ответ:

Корни уравнения: $x_1 = -4$, $x_2 = 2$.

г) $|x — 4| = 3$

Перепишем уравнение:

$$|x — 4| = 3$$

Мы имеем модуль, который равен 3. Модуль принимает два значения:

• $x — 4 = 3$ (положительное выражение внутри модуля),
• $x — 4 = -3$ (отрицательное выражение внутри модуля).

Решим оба случая:

• Для $x — 4 = 3$:

  $$x = 3 + 4 = 7$$

• Для $x — 4 = -3$:

  $$x = -3 + 4 = 1$$

Ответ:

Корни уравнения: $x_1 = 1$, $x_2 = 7$.

Итоговый ответ:

а) Корни уравнения: $x_1 = -2$, $x_2 = 6$.

б) Корни уравнения: $x_1 = -8$, $x_2 = 2$.

в) Корни уравнения: $x_1 = -4$, $x_2 = 2$.

г) Корни уравнения: $x_1 = 1$, $x_2 = 7$.