ГДЗ по Алгебре 10 Класс Номер 107 Повторение Профильный Уровень Мордкович — Подробные Ответы

Постройте график уравнения:

а) $x^2+y^2=1$

б) $(x-1{)}^2+y^2=9$

в) $x^2+(y+2{)}^2=25$

г) $(x+3{)}^2+(y-2{)}^2=4$

Все уравнения в данном задании описывают окружности.

а) $x^2+y^2=1$

Координаты центра окружности:

$$x_0=0\text{и}{y}_0=0$$

Радиус окружности:

$$R=\sqrt{1}=1$$

График уравнения:

б) $(x-1{)}^2+y^2=9$

Координаты центра окружности:

$$x_0=1\text{и}{y}_0=0$$

Радиус окружности:

$$R=\sqrt{9}=3$$

График уравнения:

в) $x^2+(y+2{)}^2=25$

Координаты центра окружности:

$$x_0=0\text{и}{y}_0=-2$$

Радиус окружности:

$$R=\sqrt{25}=5$$

График уравнения:

г) $(x+3{)}^2+(y-2{)}^2=4$

Координаты центра окружности:

$$x_0=-3\text{и}{y}_0=2$$

Радиус окружности:

$$R=\sqrt{4}=2$$

График уравнения:

Все уравнения в данном задании описывают окружности. Окружность на плоскости можно описать уравнением вида:

$$(x-x_0{)}^2+(y-y_0{)}^2=R^2$$

где $(x_0,y_0)$ — координаты центра окружности, а $R$ — радиус окружности. В зависимости от того, как уравнение записано, необходимо преобразовать его в такую форму, чтобы можно было легко определить центр и радиус окружности.

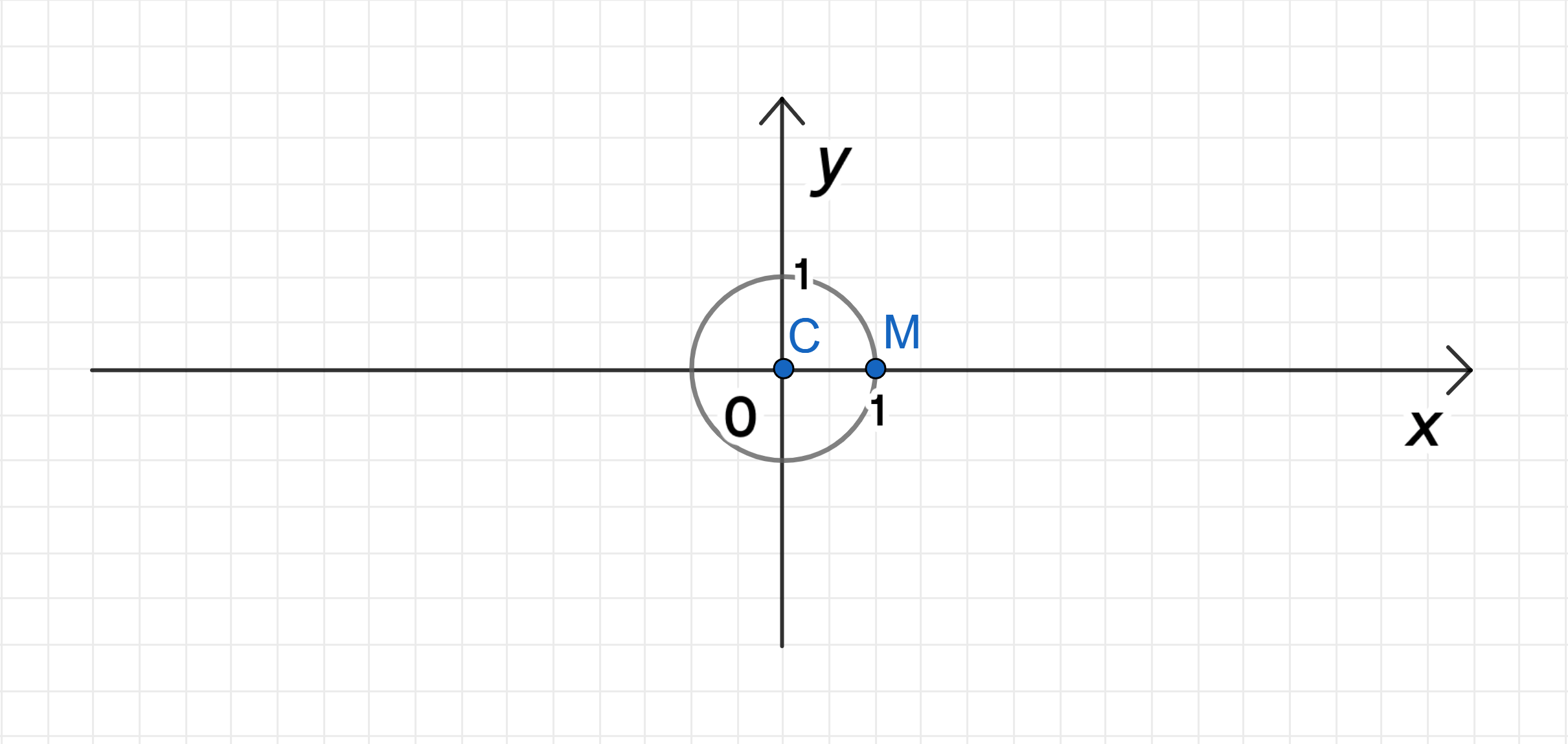
а) Уравнение: $x^2+y^2=1$

Координаты центра окружности:

Это уравнение уже записано в стандартной форме, где $(x_0,y_0)$ — это центр окружности, а $R^2$ — квадрат радиуса.

В данном случае:

$$x^2+y^2=1$$

можно воспринимать как $(x-0{)}^2+(y-0{)}^2=1^2$, то есть:

• Центр окружности $(x_0,y_0)=(0,0)$.

Радиус окружности:

Радиус окружности $R$ равен квадратному корню из правой части уравнения:

$$R=\sqrt{1}=1$$

Таким образом, радиус окружности $R=1$.

График уравнения:

Уравнение $x^2+y^2=1$ описывает окружность с центром в начале координат и радиусом 1.

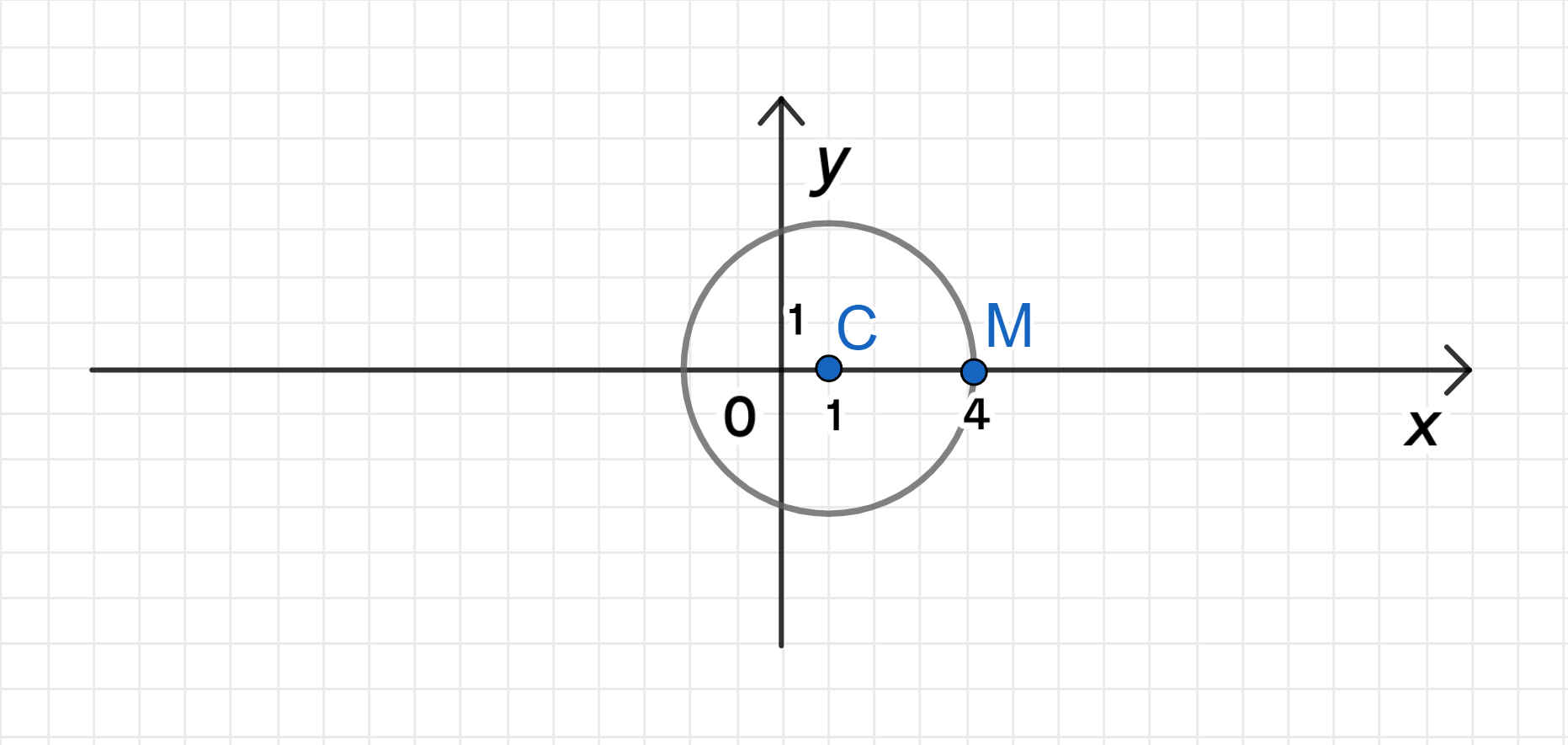
б) Уравнение: $(x-1{)}^2+y^2=9$

Координаты центра окружности:

Это уравнение тоже записано в стандартной форме. Здесь мы видим, что $(x-1{)}^2+y^2=9$ можно интерпретировать как $(x-x_0{)}^2+(y-y_0{)}^2=R^2$, где:

• $x_0=1$,
• $y_0=0$.

Следовательно, центр окружности находится в точке $(1,0)$.

Радиус окружности:

Для нахождения радиуса нужно извлечь квадратный корень из правой части уравнения:

$$R=\sqrt{9}=3$$

Таким образом, радиус окружности $R=3$.

График уравнения:

Уравнение $(x-1{)}^2+y^2=9$ описывает окружность с центром в точке $(1,0)$ и радиусом 3.

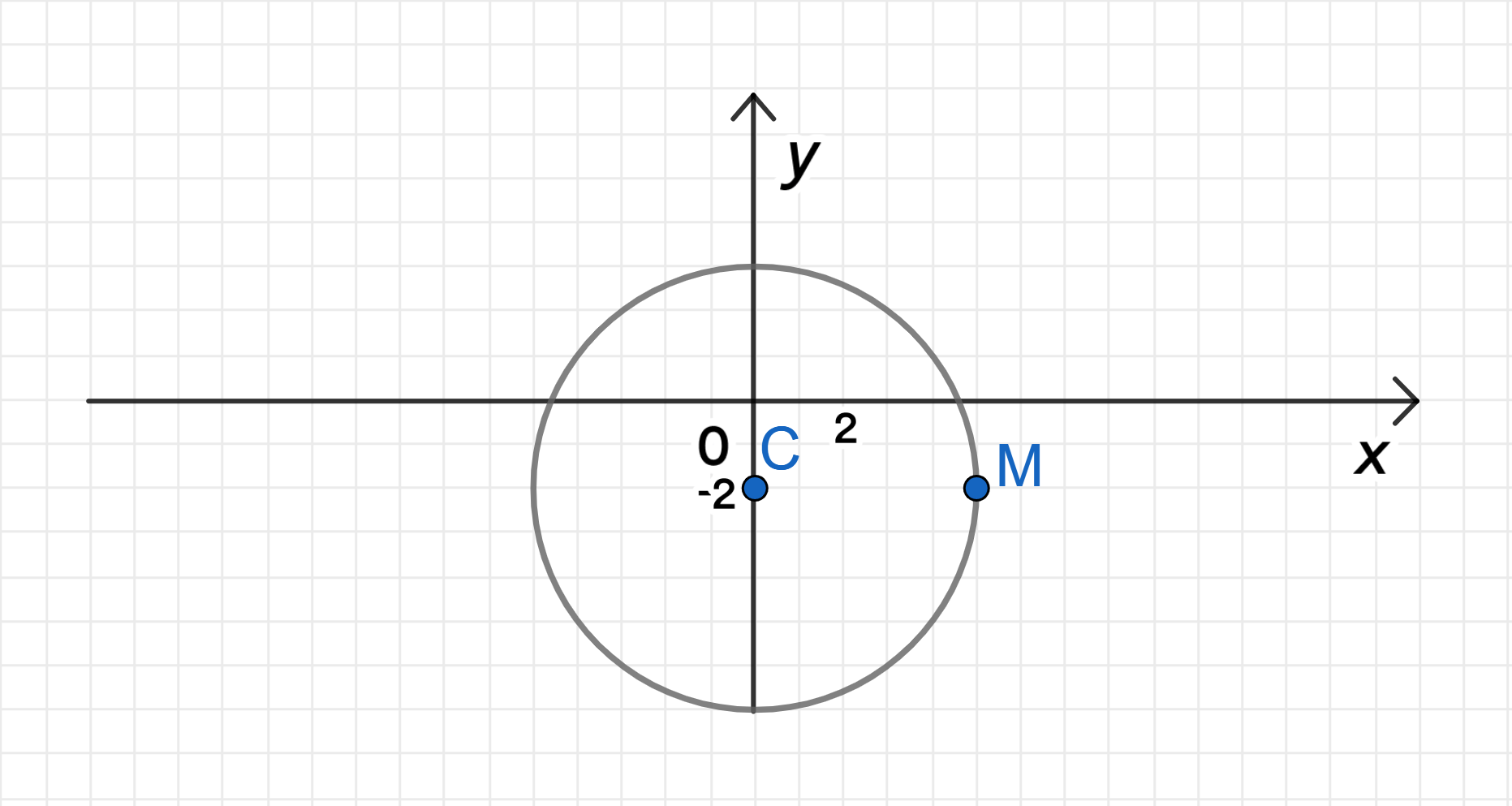
в) Уравнение: $x^2+(y+2{)}^2=25$

Координаты центра окружности:

Уравнение $x^2+(y+2{)}^2=25$ также имеет стандартную форму, но с сдвигом по оси $y$. Мы можем записать его как:

$$(x-0{)}^2+(y-(-2){)}^2=25$$

Таким образом:

• Центр окружности $(x_0,y_0)=(0,-2)$.

Радиус окружности:

Радиус $R$ находим, извлекая квадратный корень из правой части уравнения:

$$R=\sqrt{25}=5$$

Таким образом, радиус окружности $R=5$.

График уравнения:

Уравнение $x^2+(y+2{)}^2=25$ описывает окружность с центром в точке $(0,-2)$ и радиусом 5.

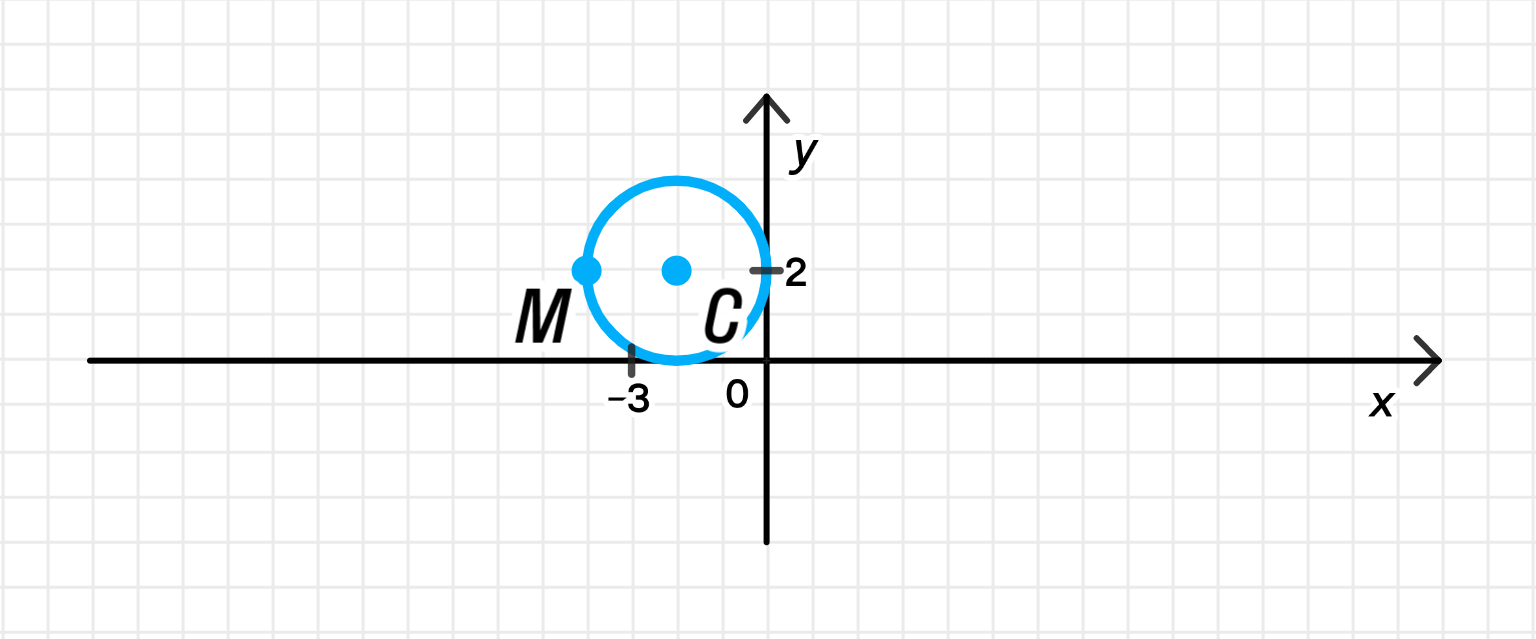
г) Уравнение: $(x+3{)}^2+(y-2{)}^2=4$

Координаты центра окружности:

В уравнении $(x+3{)}^2+(y-2{)}^2=4$ видим, что оно записано в форме $(x-x_0{)}^2+(y-y_0{)}^2=R^2$. Сравнив, можно выделить:

• $x_0=-3$,
• $y_0=2$.

Следовательно, центр окружности находится в точке $(-3,2)$.

Радиус окружности:

Радиус $R$ вычисляем, извлекая квадратный корень из правой части уравнения:

$$R=\sqrt{4}=2$$

Таким образом, радиус окружности $R=2$.

График уравнения:

Уравнение $(x+3{)}^2+(y-2{)}^2=4$ описывает окружность с центром в точке $(-3,2)$ и радиусом 2.

Для каждой окружности мы:

1. Привели уравнение к стандартной форме $(x-x_0{)}^2+(y-y_0{)}^2=R^2$.
2. Определили координаты центра $(x_0,y_0)$ и радиус $R$.
3. Представили графики каждой окружности.