ГДЗ по Алгебре 10 Класс Номер 11.10 Профильный Уровень Мордкович — Подробные Ответы

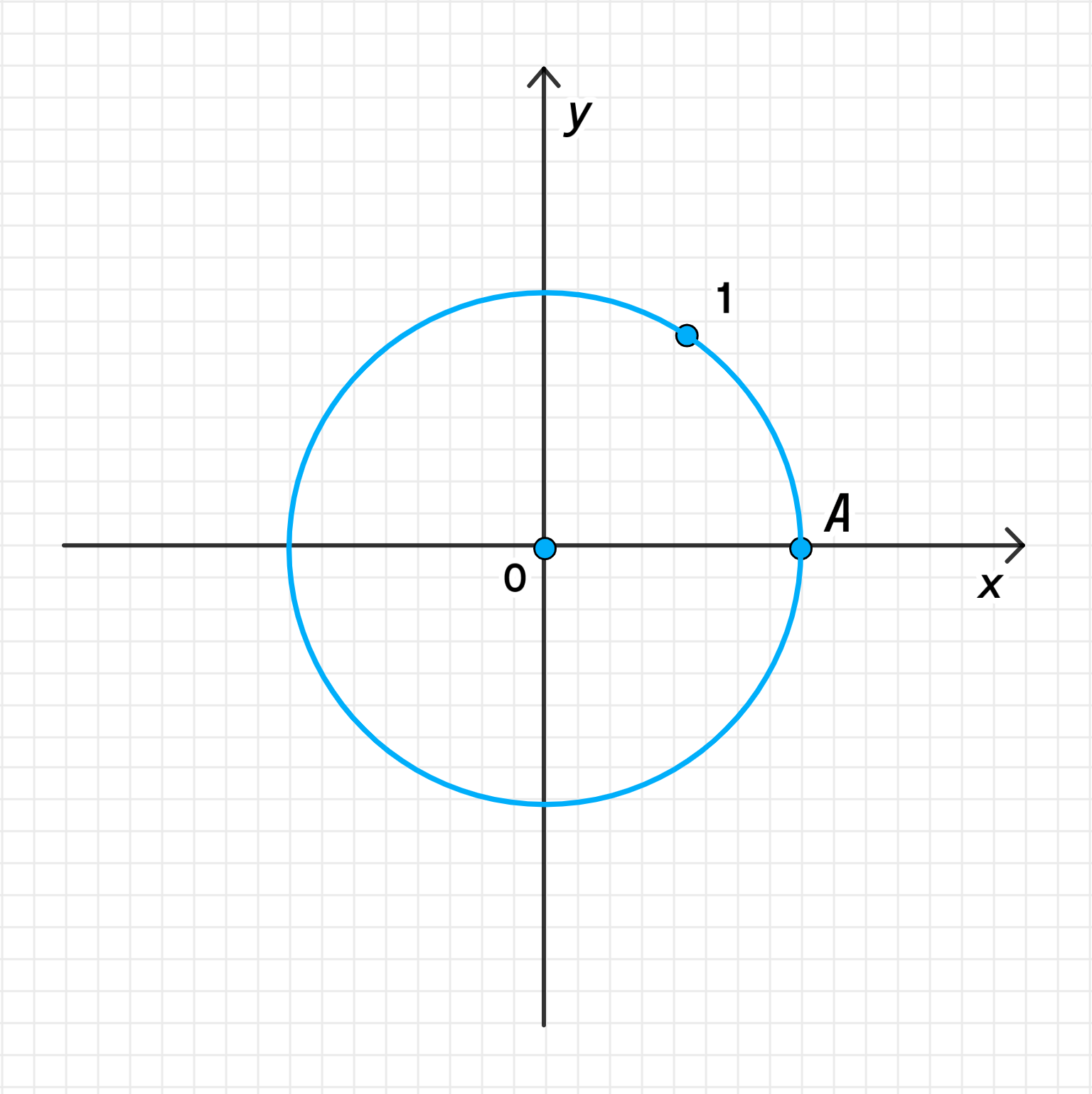
а) 1

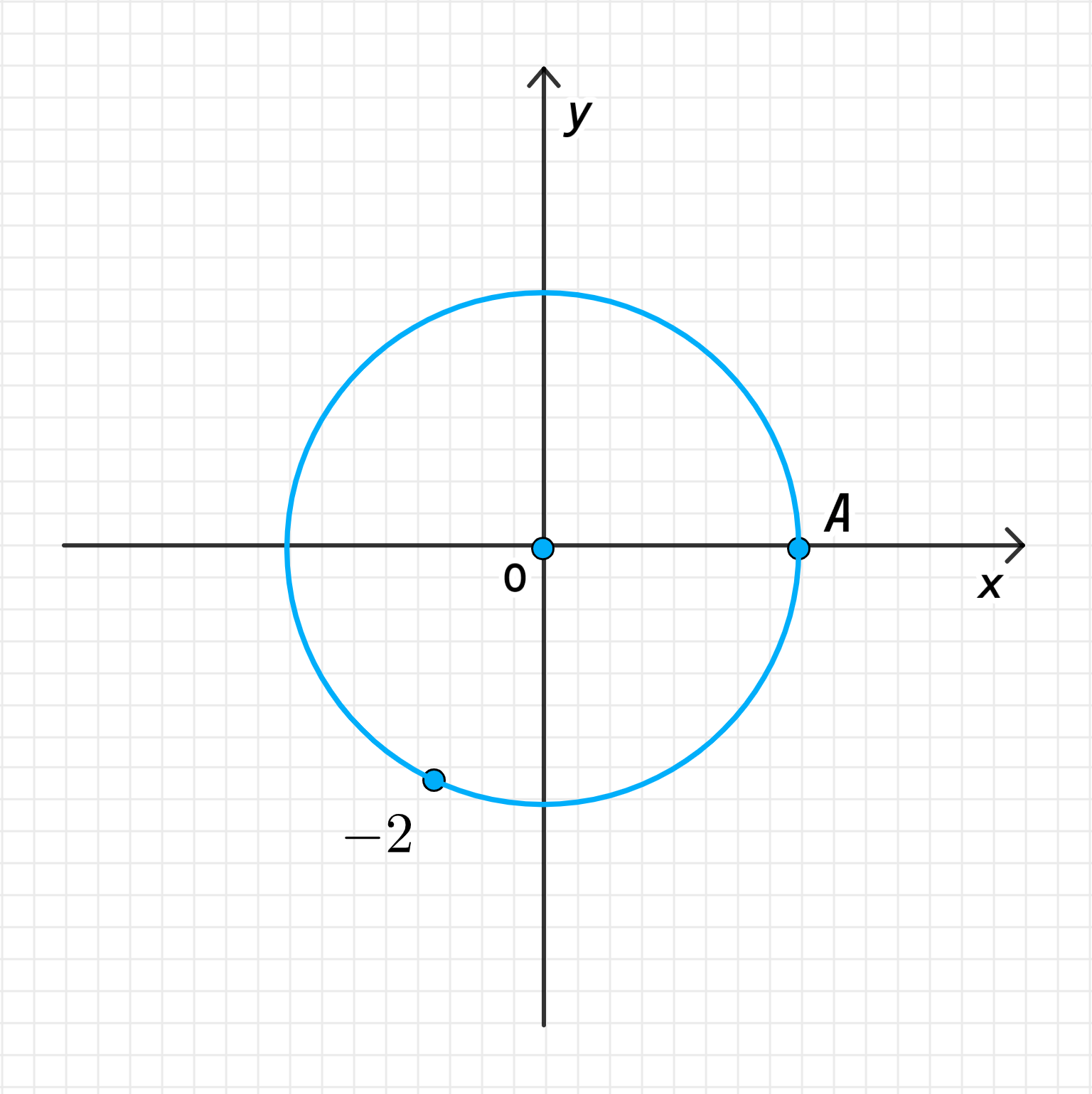
б) -2

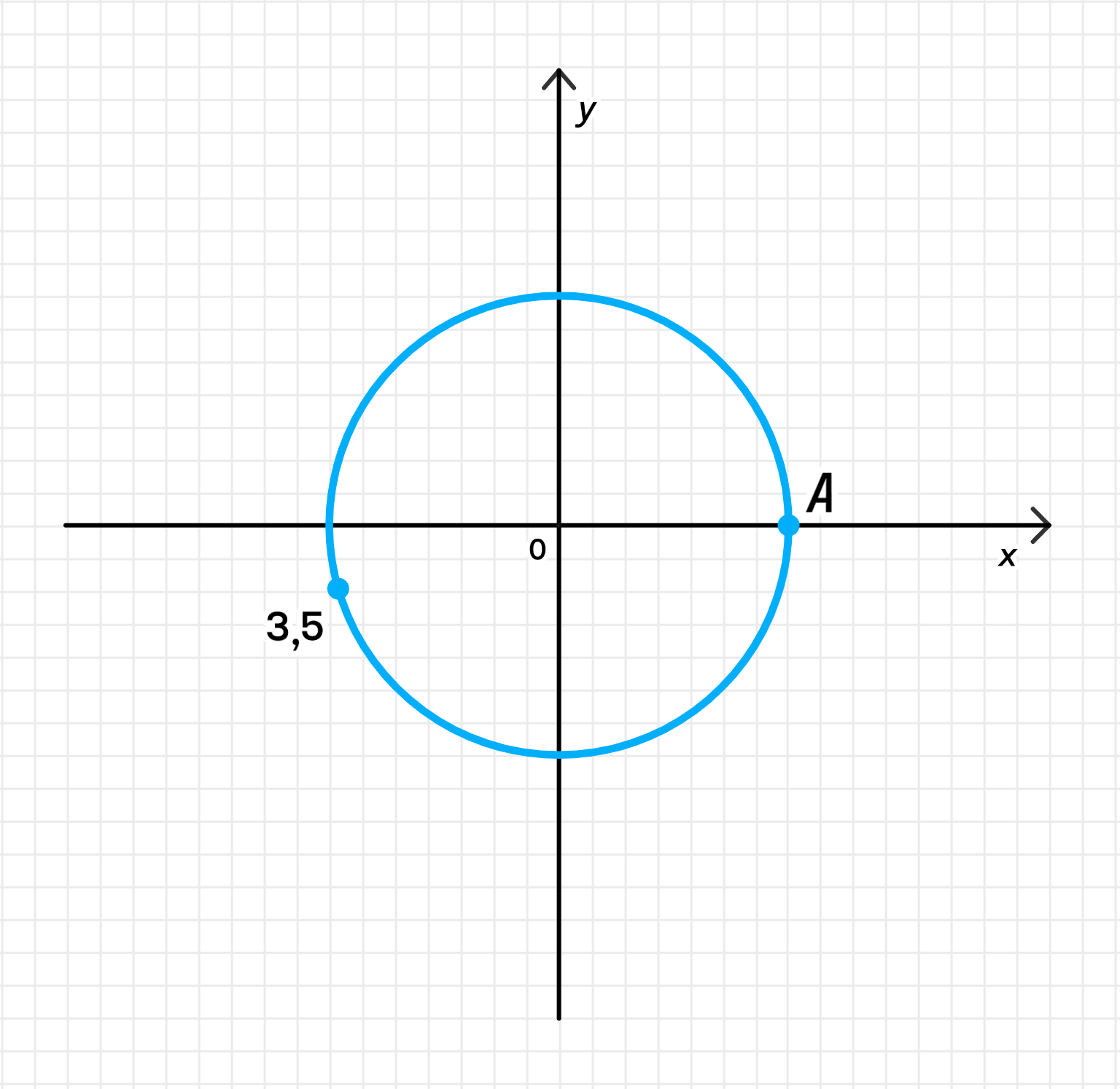
в) 3,5

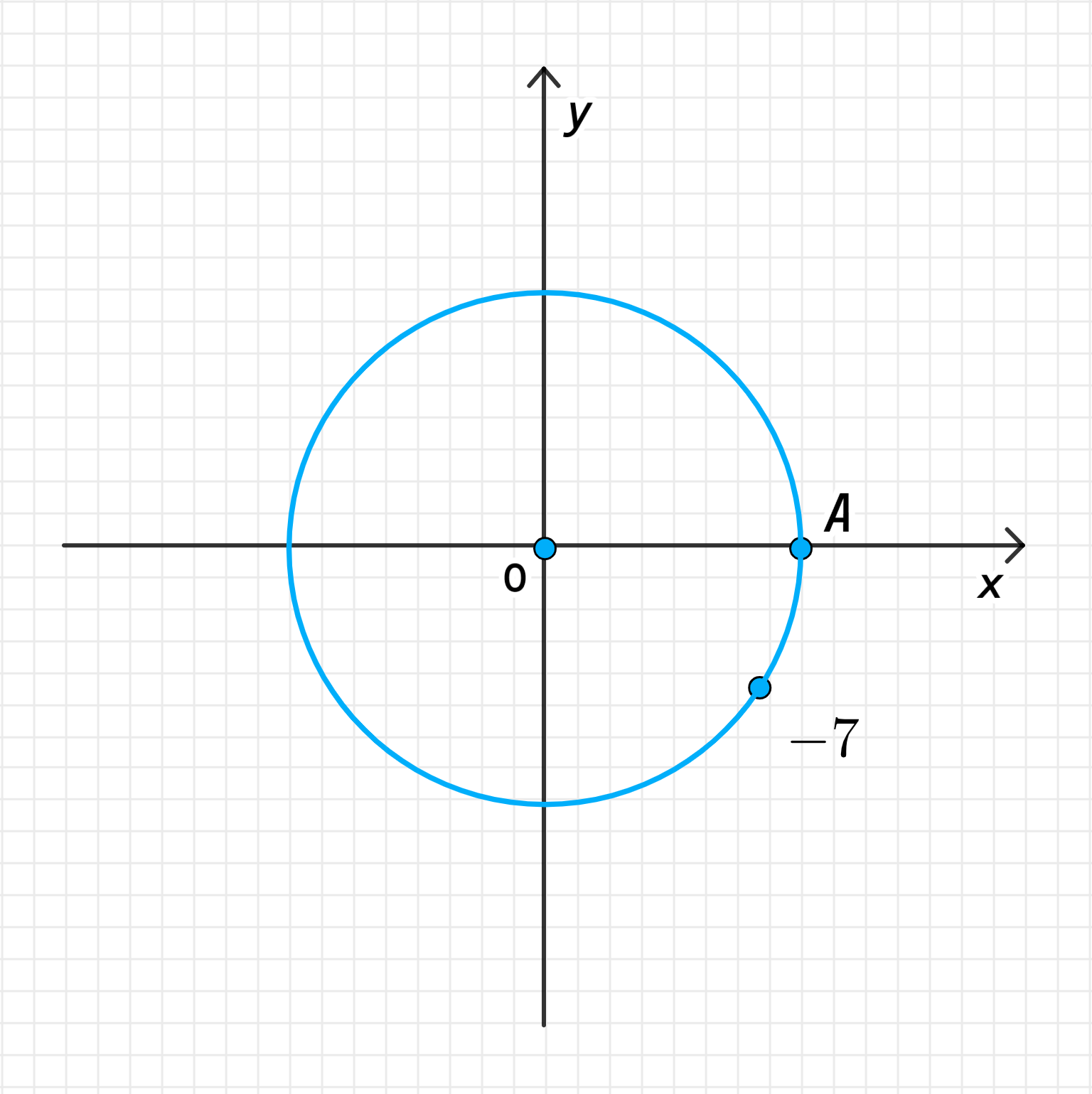
г) -7

а) Число 1;

Наиболее близкое значение угла:

$$\frac{\pi}{3} \approx 1,047;$$

Соответствует повороту точки $A$ на угол $\frac{\pi}{3}$ против часовой стрелки;

То есть ближайшая к искомой точка $M$ делит дугу $AB$ в отношении:

$$\frac{AM}{AB} = \frac{\pi}{3} : \frac{\pi}{2} = \frac{\pi}{3} \cdot \frac{2}{\pi} = \frac{2}{3};$$

Искомая точка $N$ находится немного ближе:

б) Число (-2);

Наиболее близкое значение угла:

$$-\frac{2\pi}{3} \approx -2,094;$$ $$a = 2\pi — \frac{2\pi}{3} = \frac{4\pi}{3} = \pi + \frac{\pi}{3};$$

Соответствует повороту точки $C$ на угол $\frac{\pi}{3}$ против часовой стрелки;

То есть ближайшая к искомой точка $M$ делит дугу $CD$ в отношении:

$$\frac{CM}{CD} = \frac{\pi}{3} : \frac{\pi}{2} = \frac{\pi}{3} \cdot \frac{2}{\pi} = \frac{2}{3};$$

Искомая точка $N$ находится немного дальше:

в) Число 3,5;

Наиболее близкое значение угла:

$$\frac{9\pi}{8} \approx 3,534;$$ $$a = \frac{9\pi}{8} = \pi + \frac{\pi}{8};$$

Соответствует повороту точки $C$ на угол $\frac{\pi}{8}$ против часовой стрелки;

То есть ближайшая к искомой точка $M$ делит дугу $CD$ в отношении:

$$\frac{CM}{CD} = \frac{\pi}{8} : \frac{\pi}{2} = \frac{\pi}{8} \cdot \frac{2}{\pi} = \frac{2}{8} = \frac{1}{4};$$

Искомая точка $N$ находится немного ближе:

г) Число (-7);

Наиболее близкое значение угла:

$$-\frac{9\pi}{4} \approx -7,068;$$ $$a = 4\pi — \frac{9\pi}{4} = \frac{7\pi}{4} = \frac{6\pi}{4} + \frac{\pi}{4} = \frac{3\pi}{2} + \frac{\pi}{4};$$

Соответствует повороту точки $D$ на угол $\frac{\pi}{4}$ против часовой стрелки;

То есть ближайшая к искомой точка $M$ делит дугу $DA$ в отношении:

$$\frac{DM}{DA} = \frac{\pi}{4} : \frac{\pi}{2} = \frac{\pi}{4} \cdot \frac{2}{\pi} = \frac{2}{4} = \frac{1}{2};$$

Искомая точка $N$ находится немного дальше:

а) Число 1;

1. Наиболее близкое значение угла:

   Число 1 близко к углу, который можно выразить в радианах как $\frac{\pi}{3}$, так как:

   $$\frac{\pi}{3} \approx 1,047.$$

   Таким образом, числовое значение угла, наиболее близкое к 1, равно $\frac{\pi}{3}$.

2. Поворот точки $A$ на угол $\frac{\pi}{3}$:

   Поворот точки $A$ на угол $\frac{\pi}{3}$ против часовой стрелки означает, что точка $A$ будет перемещаться по окружности на угол в $60^\circ$ против часовой стрелки, что составляет $\frac{\pi}{3}$ радиан.

3. Деление дуги $AB$:

   Дуга $AB$ между точками $A$ и $B$ составляет угол $\frac{\pi}{2}$ радиан, или $90^\circ$. Когда точка $A$ перемещается на угол $\frac{\pi}{3}$, она делит дугу $AB$ в следующем отношении:

   $$\frac{AM}{AB} = \frac{\frac{\pi}{3}}{\frac{\pi}{2}} = \frac{\pi}{3} \cdot \frac{2}{\pi} = \frac{2}{3}.$$

   Это означает, что точка $M$ будет находиться на $\frac{2}{3}$ пути от точки $A$ до точки $B$.

4. Искомая точка $N$:

   Поскольку $M$ делит дугу $AB$ в отношении $\frac{2}{3}$, точка $N$ будет находиться немного ближе к точке $A$, так как угол поворота $1$ близок, но немного меньше, чем $\frac{\pi}{3}$.

б) Число (-2);

1. Наиболее близкое значение угла:

   Число $-2$ эквивалентно углу, равному $-\frac{2\pi}{3}$, так как:

   $$-\frac{2\pi}{3} \approx -2,094.$$

   Это значение угла находится между углами $-\pi$ и $0$, и близко к углу $-\frac{2\pi}{3}$, который эквивалентен повороту по часовой стрелке.

2. Приведение угла к положительному эквиваленту:

   Чтобы перевести отрицательный угол $-\frac{2\pi}{3}$ в положительное направление, добавляем полный оборот $2\pi$:

   $$a = 2\pi — \frac{2\pi}{3} = \frac{4\pi}{3} = \pi + \frac{\pi}{3}.$$

   Это означает, что угол $-\frac{2\pi}{3}$ эквивалентен повороту на угол $\frac{\pi}{3}$ против часовой стрелки.

3. Поворот точки $C$ на угол $\frac{\pi}{3}$:

   Поворот точки $C$ на угол $\frac{\pi}{3}$ против часовой стрелки означает, что точка $C$ переместится по окружности на угол $\frac{\pi}{3}$ (или $60^\circ$) против часовой стрелки.

4. Деление дуги $CD$:

   Дуга $CD$ между точками $C$ и $D$ составляет угол $\frac{\pi}{2}$. Точка $M$ делит эту дугу в отношении:

   $$\frac{CM}{CD} = \frac{\frac{\pi}{3}}{\frac{\pi}{2}} = \frac{\pi}{3} \cdot \frac{2}{\pi} = \frac{2}{3}.$$

   Это означает, что точка $M$ находится на $\frac{2}{3}$ пути от точки $C$ до точки $D$.

5. Искомая точка $N$:

   Так как $M$ делит дугу $CD$ в отношении $\frac{2}{3}$, точка $N$ будет находиться немного дальше от точки $C$, так как угол поворота $-2$ больше, чем угол $\frac{\pi}{3}$.

в) Число 3,5;

1. Наиболее близкое значение угла:

   Число $3,5$ эквивалентно углу $\frac{9\pi}{8}$, так как:

   $$\frac{9\pi}{8} \approx 3,534.$$

   Это значение угла немного больше, чем $\pi$, но меньше, чем $2\pi$.

2. Приведение угла $\frac{9\pi}{8}$:

   Угол $\frac{9\pi}{8}$ можно выразить как:

   $$a = \frac{9\pi}{8} = \pi + \frac{\pi}{8}.$$

   Это эквивалентно повороту на угол $\frac{\pi}{8}$ против часовой стрелки после одного полного оборота.

3. Поворот точки $C$ на угол $\frac{\pi}{8}$:

   Поворот точки $C$ на угол $\frac{\pi}{8}$ против часовой стрелки будет происходить на угол всего лишь $22,5^\circ$, что является маленьким поворотом.

4. Деление дуги $CD$:

   Дуга $CD$ составляет $\frac{\pi}{2}$ радиан. Точка $M$ делит эту дугу в отношении:

   $$\frac{CM}{CD} = \frac{\frac{\pi}{8}}{\frac{\pi}{2}} = \frac{\pi}{8} \cdot \frac{2}{\pi} = \frac{2}{8} = \frac{1}{4}.$$

   Это означает, что точка $M$ будет находиться на $\frac{1}{4}$-м пути от точки $C$ до точки $D$.

5. Искомая точка $N$:

   Поскольку $M$ делит дугу $CD$ в отношении $\frac{1}{4}$, точка $N$ будет находиться немного ближе к точке $C$.

г) Число (-7);

1. Наиболее близкое значение угла:

   Число $-7$ эквивалентно углу $-\frac{9\pi}{4}$, так как:

   $$-\frac{9\pi}{4} \approx -7,068.$$

   Это значение угла является отрицательным и больше, чем $-2\pi$, но меньше, чем $-\pi$.

2. Приведение угла $-\frac{9\pi}{4}$ к положительному эквиваленту:

   Чтобы перевести этот угол в положительный эквивалент, добавим $2\pi$ дважды:

   $$a = 4\pi — \frac{9\pi}{4} = \frac{7\pi}{4} = \frac{6\pi}{4} + \frac{\pi}{4} = \frac{3\pi}{2} + \frac{\pi}{4}.$$

   Это эквивалентно повороту на угол $\frac{\pi}{4}$ против часовой стрелки.

3. Поворот точки $D$ на угол $\frac{\pi}{4}$:

   Поворот точки $D$ на угол $\frac{\pi}{4}$ против часовой стрелки переместит точку $D$ на угол $\frac{\pi}{4}$ (или 45 градусов).

4. Деление дуги $DA$:

   Дуга $DA$ составляет $\frac{\pi}{2}$. Точка $M$ делит дугу $DA$ в отношении:

   $$\frac{DM}{DA} = \frac{\frac{\pi}{4}}{\frac{\pi}{2}} = \frac{\pi}{4} \cdot \frac{2}{\pi} = \frac{2}{4} = \frac{1}{2}.$$

   Это означает, что точка $M$ будет находиться в середине дуги $DA$.

5. Искомая точка $N$:

   Поскольку точка $M$ делит дугу $DA$ пополам, точка $N$ будет находиться немного дальше от точки $D$.