ГДЗ по Алгебре 10 Класс Номер 11.2 Профильный Уровень Мордкович — Подробные Ответы

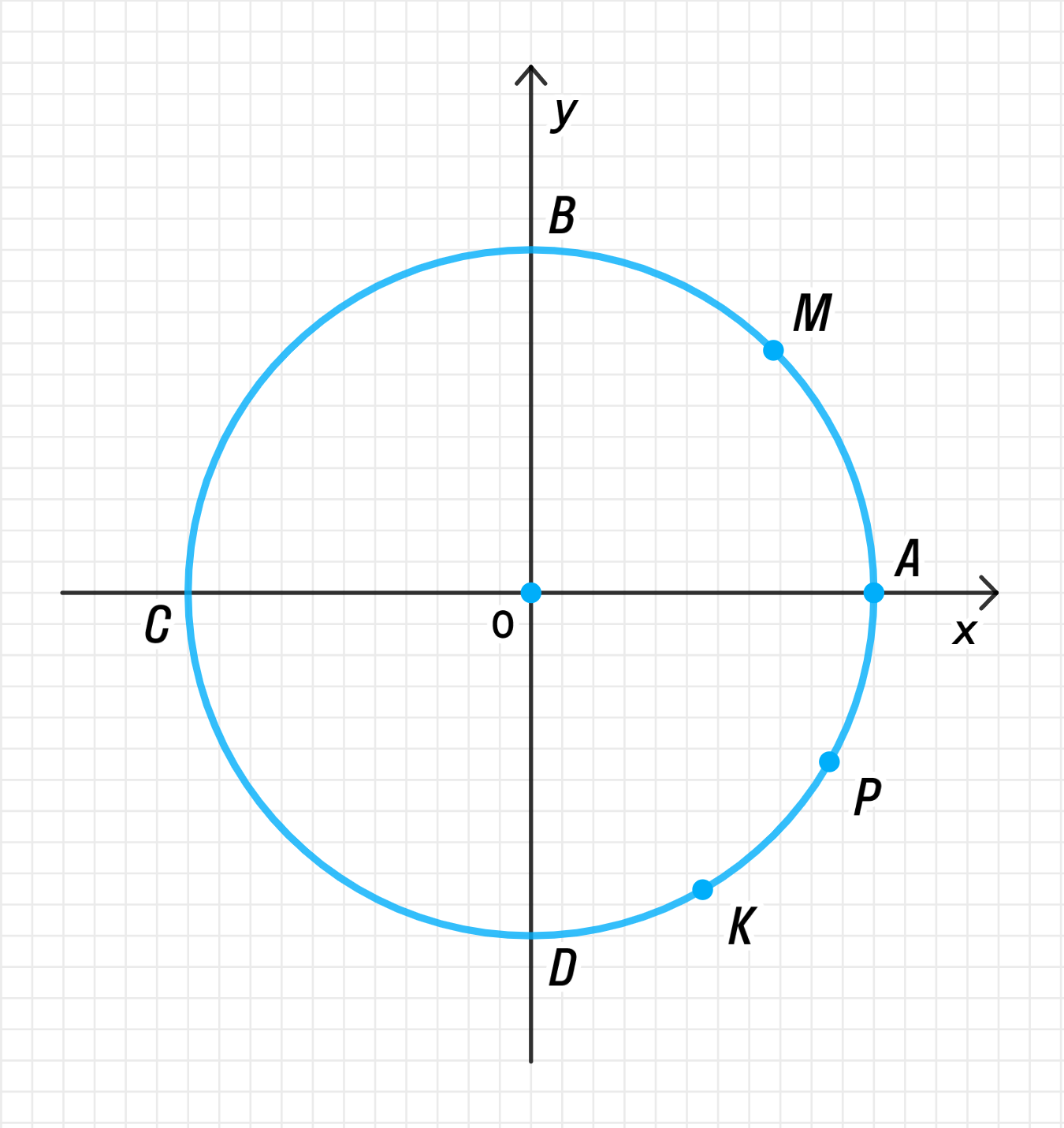
Первая четверть разделена на две равные части точкой M, а четвертая — на три равные части точками K и Р. Найдите длину дуги:

а) DM;

б) BK;

в) PM;

г) PC.

Первая четверть разделена на две равные части точкой $M$, а четвертая — на три равные части точками $K$ и $P$:

а) Длина дуги $DM$:

$$AM = \frac{AB}{2} = \frac{\pi}{2} : 2 = \frac{\pi}{4};$$ $$DM = DA + AM = \frac{\pi}{2} + \frac{\pi}{4} = \frac{2\pi}{4} + \frac{\pi}{4} = \frac{3\pi}{4};$$

Ответ: $\frac{3\pi}{4}$.

б) Длина дуги $BK$:

$$DK = \frac{DA}{3} = \frac{\pi}{2} : 3 = \frac{\pi}{6};$$ $$BK = BD + DK = \pi + \frac{\pi}{6} = \frac{6\pi}{6} + \frac{\pi}{6} = \frac{7\pi}{6};$$

Ответ: $\frac{7\pi}{6}$.

в) Длина дуги $PM$:

$$PA = \frac{DA}{3} = \frac{\pi}{2} : 3 = \frac{\pi}{6};$$ $$AM = \frac{AB}{2} = \frac{\pi}{2} : 2 = \frac{\pi}{4};$$ $$PM = PA + AM = \frac{\pi}{6} + \frac{\pi}{4} = \frac{2\pi}{12} + \frac{3\pi}{12} = \frac{5\pi}{12};$$

Ответ: $\frac{5\pi}{12}$.

г) Длина дуги $PC$:

$$PA = \frac{DA}{3} = \frac{\pi}{2} : 3 = \frac{\pi}{6};$$ $$PC = PA + AC = \frac{\pi}{6} + \pi = \frac{\pi}{6} + \frac{6\pi}{6} = \frac{7\pi}{6};$$

Ответ: $\frac{7\pi}{6}$.

Первая четверть разделена на две равные части точкой $M$, а четвертая — на три равные части точками $K$ и $P$.

Пусть окружность имеет радиус $r = 1$, и её полная длина составляет $2\pi$. В первой четверти окружности длина пути будет составлять $\frac{\pi}{2}$, поскольку она составляет четвертую часть от общей длины окружности. Точно так же, в четвертой четверти длина дуги составляет также $\frac{\pi}{2}$.

а) Длина дуги $DM$:

Дуга $AM$:

Первая четверть окружности разделена на две равные части точкой $M$. Следовательно, длина дуги $AM$ равна половине длины всей первой четверти. Поскольку вся первая четверть окружности составляет $\frac{\pi}{2}$, то длина дуги $AM$ будет равна:

$$AM = \frac{AB}{2} = \frac{\pi}{2} : 2 = \frac{\pi}{4}$$

Дуга $DM$:

Дуга $DM$ состоит из двух частей:

• Дуга от $D$ до $A$, которая составляет $\frac{\pi}{2}$ (так как это целая первая четверть),
• Дуга от $A$ до $M$, которая равна $\frac{\pi}{4}$, как мы только что вычислили.

Таким образом, длина дуги $DM$ будет равна сумме этих двух отрезков:

$$DM = DA + AM = \frac{\pi}{2} + \frac{\pi}{4}$$

Приводим к общему знаменателю:

$$DM = \frac{2\pi}{4} + \frac{\pi}{4} = \frac{3\pi}{4}$$

Ответ: длина дуги $DM$ равна $\frac{3\pi}{4}$.

б) Длина дуги $BK$:

Дуга $DK$:

Четвертая четверть круга разделена на три равные части точками $K$ и $P$. Поскольку длина всей четвертой четверти равна $\frac{\pi}{2}$, длина каждой из этих частей будет:

$$DK = \frac{DA}{3} = \frac{\pi}{2} : 3 = \frac{\pi}{6}$$

Дуга $BK$:

Дуга $BK$ состоит из двух частей:

• Дуга от $B$ до $D$, которая составляет $\pi$ (это половина окружности, т.е. полная длина от $B$ до $D$),
• Дуга от $D$ до $K$, которая равна $\frac{\pi}{6}$, как мы только что вычислили.

Сложим эти два отрезка:

$$BK = BD + DK = \pi + \frac{\pi}{6}$$

Приводим к общему знаменателю:

$$BK = \frac{6\pi}{6} + \frac{\pi}{6} = \frac{7\pi}{6}$$

Ответ: длина дуги $BK$ равна $\frac{7\pi}{6}$.

в) Длина дуги $PM$:

Дуга $PA$:

Дуга $PA$ — это часть четвертой четверти, которая делится на три равные части точкой $P$. Поскольку длина четвертой четверти составляет $\frac{\pi}{2}$, длина одной из этих частей будет:

$$PA = \frac{DA}{3} = \frac{\pi}{2} : 3 = \frac{\pi}{6}$$

Дуга $AM$:

Дуга $AM$ — это половина первой четверти окружности, как мы вычисляли ранее. Она равна:

$$AM = \frac{AB}{2} = \frac{\pi}{2} : 2 = \frac{\pi}{4}$$

Дуга $PM$:

Дуга $PM$ состоит из двух частей:

• Дуга от $P$ до $A$, которая равна $\frac{\pi}{6}$,
• Дуга от $A$ до $M$, которая равна $\frac{\pi}{4}$.

Сложим эти два отрезка:

$$PM = PA + AM = \frac{\pi}{6} + \frac{\pi}{4}$$

Приводим к общему знаменателю:

$$PM = \frac{2\pi}{12} + \frac{3\pi}{12} = \frac{5\pi}{12}$$

Ответ: длина дуги $PM$ равна $\frac{5\pi}{12}$.

г) Длина дуги $PC$:

Дуга $PA$:

Дуга $PA$ уже вычислена ранее, и её длина равна $\frac{\pi}{6}$.

Дуга $AC$:

Дуга $AC$ — это оставшаяся часть четвертой четверти. Поскольку длина всей четвертой четверти составляет $\frac{\pi}{2}$, и длина дуги $PA$ составляет $\frac{\pi}{6}$, то длина дуги $AC$ будет:

$$AC = \frac{\pi}{2} — \frac{\pi}{6} = \frac{3\pi}{6} — \frac{\pi}{6} = \frac{2\pi}{6} = \frac{\pi}{3}$$

Дуга $PC$:

Дуга $PC$ состоит из двух частей:

• Дуга от $P$ до $A$, которая равна $\frac{\pi}{6}$,
• Дуга от $A$ до $C$, которая равна $\pi$ (половина окружности).

Сложим эти два отрезка:

$$PC = PA + AC = \frac{\pi}{6} + \pi = \frac{\pi}{6} + \frac{6\pi}{6} = \frac{7\pi}{6}$$

Ответ: длина дуги $PC$ равна $\frac{7\pi}{6}$.

Итоговые ответы:

• Длина дуги $DM$ = $\frac{3\pi}{4}$.
• Длина дуги $BK$ = $\frac{7\pi}{6}$.
• Длина дуги $PM$ = $\frac{5\pi}{12}$.
• Длина дуги $PC$ = $\frac{7\pi}{6}$.