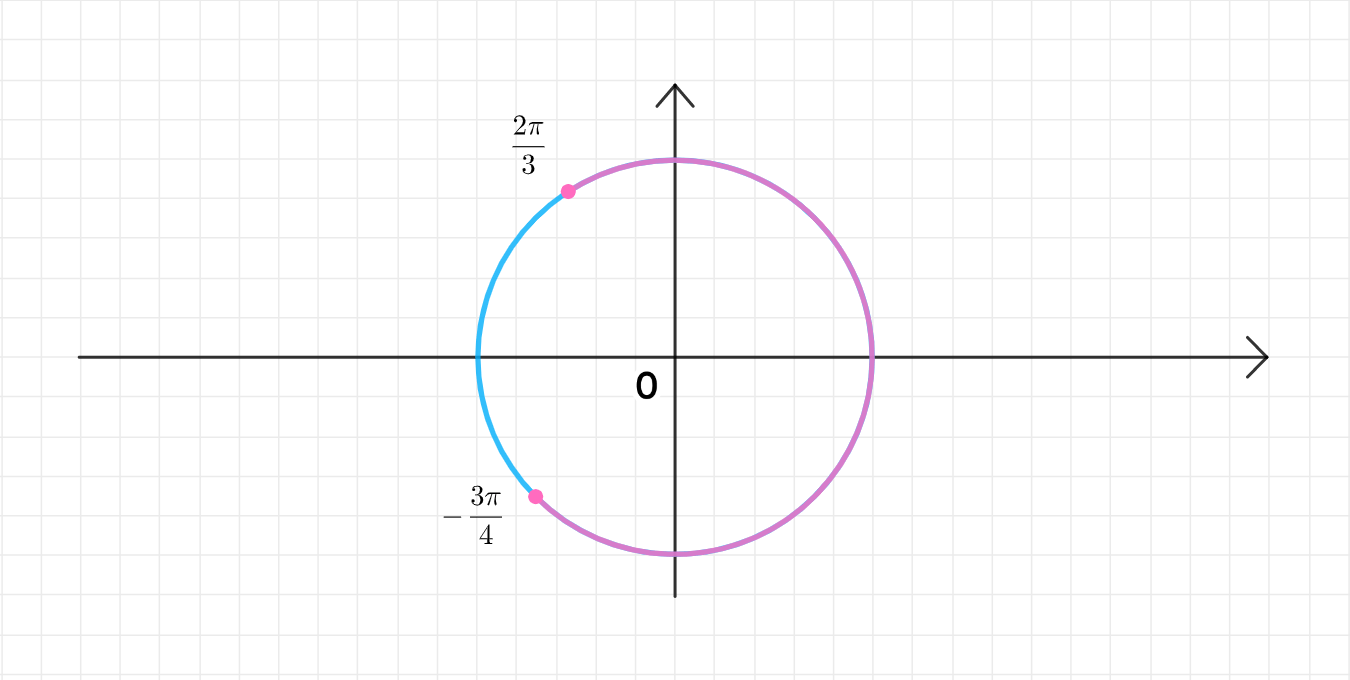ГДЗ по Алгебре 10 Класс Номер 11.28 Профильный Уровень Мордкович — Подробные Ответы

а) $-\frac{\pi }{2}+2\pi n<t<\frac{\pi }{2}+2\pi n$;

б) $-\frac{\pi }{6}+2\pi n<t<\frac{7\pi }{6}+2\pi n$;

в) $-\frac{3\pi }{4}+2\pi n<t<\frac{2\pi }{3}+2\pi n$;

г) $-\frac{\pi }{6}+2\pi n<t<\frac{5\pi }{4}+2\pi n$

а) $-\frac{\pi }{2}+2\pi n<t<\frac{\pi }{2}+2\pi n$;

На отрезке $0\le a\le 2\pi$:

$$0<a_1<\frac{\pi }{2};$$$$\frac{3\pi }{2}<a_2<2\pi ;$$

На числовой окружности:

б) $-\frac{\pi }{6}+2\pi n<t<\frac{7\pi }{6}+2\pi n$;

На отрезке $0\le a\le 2\pi$:

$$0<a_1<\frac{7\pi }{6};$$$$\frac{11\pi }{6}<a_2<2\pi ;$$

На числовой окружности:

в) $-\frac{3\pi }{4}+2\pi n<t<\frac{2\pi }{3}+2\pi n$;

На отрезке $0\le a\le 2\pi$:

$$0<a_1<\frac{2\pi }{3};$$$$\frac{5\pi }{4}<a_2<2\pi ;$$

На числовой окружности:

г) $-\frac{\pi }{6}+2\pi n<t<\frac{5\pi }{4}+2\pi n$;

На отрезке $0\le a\le 2\pi$:

$$0<a_1<\frac{5\pi }{4};$$$$\frac{11\pi }{6}<a_2<2\pi ;$$

На числовой окружности:

Задача заключается в нахождении всех точек $t$, соответствующих точкам, принадлежащим указанным дугам. Мы будем работать с интервалами углов и рассмотрим их на отрезке $0\le a\le 2\pi$ и на числовой окружности, с учётом периодичности $2\pi n$.

Длина каждой наименьшей дуги

Каждая наименьшая дуга на числовой окружности имеет длину $\frac{\pi }{6}$. Это означает, что угол между соседними точками на окружности составляет $\frac{\pi }{6}$.

Теперь давайте пошагово разберем каждую дугу, определяя интервалы для значений углов на отрезке $0\le a\le 2\pi$ и на числовой окружности.

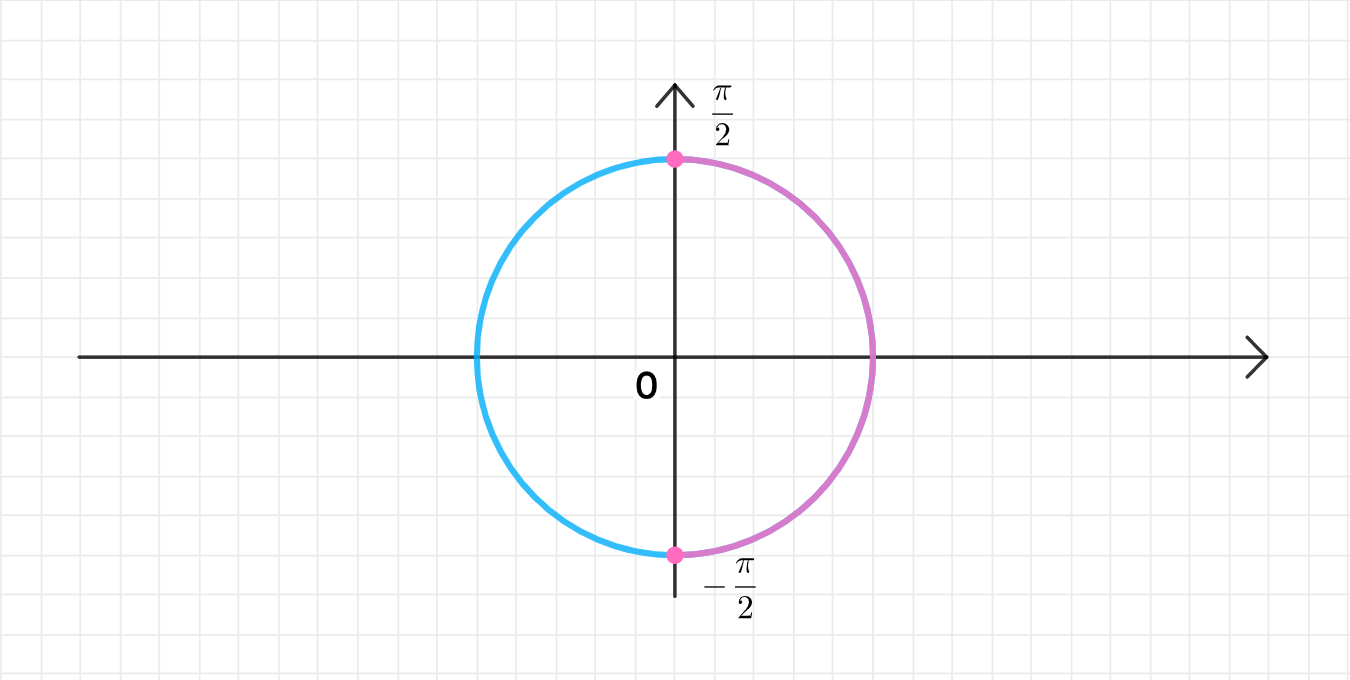
а)

Интервал:

$$-\frac{\pi }{2}+2\pi n<t<\frac{\pi }{2}+2\pi n$$

1) На отрезке $0\le a\le 2\pi$:

Нам нужно найти, какие значения углов $a$ лежат в пределах одного оборота, то есть на отрезке от $0$ до $2\pi$.

• $t=-\frac{\pi }{2}+2\pi n$ — это начало интервала, которое соответствует углу $-\frac{\pi }{2}$.
• $t=\frac{\pi }{2}+2\pi n$ — это конец интервала, который соответствует углу $\frac{\pi }{2}$.

Интервал на отрезке $0\le a\le 2\pi$ можно разделить на два:

Значения $a_1$ лежат от $0$ до $\frac{\pi }{2}$, то есть:

$$0<a_1<\frac{\pi }{2}\mathrm{.}$$

Значения $a_2$ лежат от $\frac{3\pi }{2}$ до $2\pi$, то есть:

$$\frac{3\pi }{2}<a_2<2\pi \mathrm{.}$$

2) На числовой окружности:

Поскольку окружность периодична, интервал для значений $t$ будет:

$$-\frac{\pi }{2}+2\pi n<t<\frac{\pi }{2}+2\pi n\mathrm{.}$$

Ответ для части (а):

$$-\frac{\pi }{3}+2\pi n<t<\frac{\pi }{3}+2\pi n\mathrm{.}$$

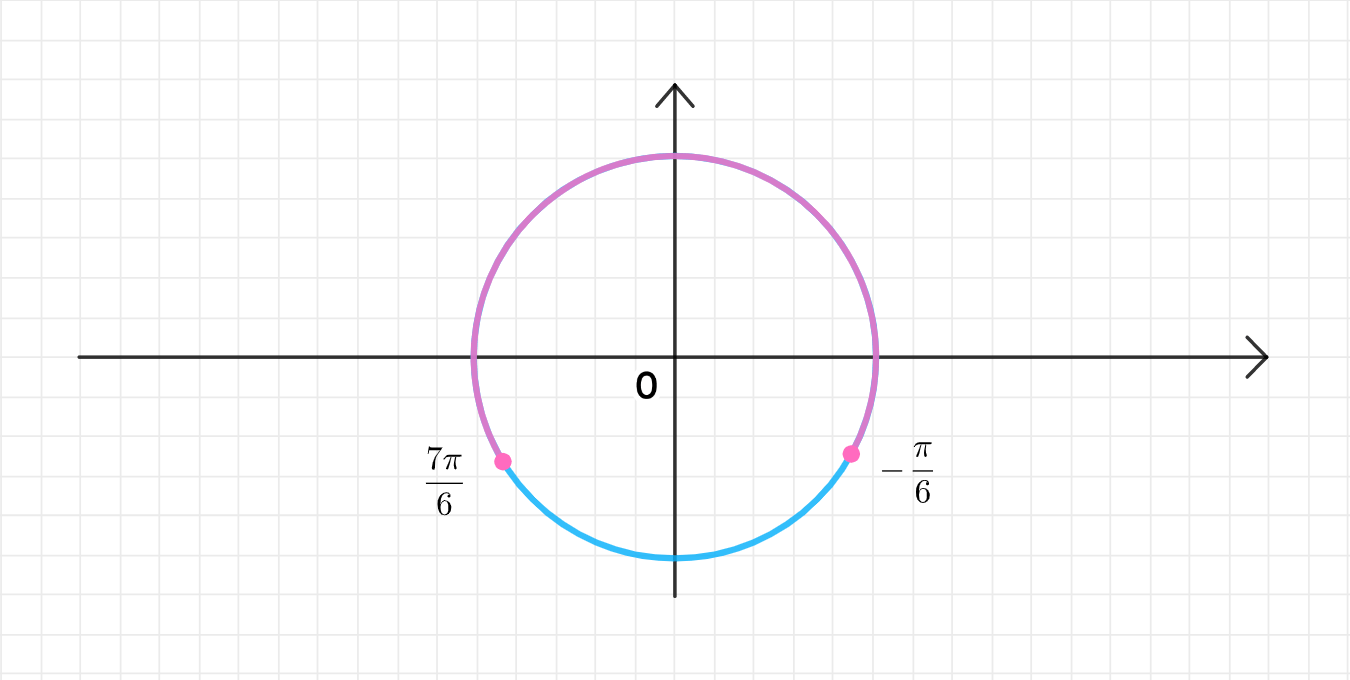
б)

Интервал:

$$-\frac{\pi }{6}+2\pi n<t<\frac{7\pi }{6}+2\pi n$$

1) На отрезке $0\le a\le 2\pi$:

Для интервала от $-\frac{\pi }{6}$ до $\frac{7\pi }{6}$, разделим его на два промежутка:

Значения $a_1$ лежат от $0$ до $\frac{7\pi }{6}$, то есть:

$$0<a_1<\frac{7\pi }{6}\mathrm{.}$$

Значения $a_2$ лежат от $\frac{11\pi }{6}$ до $2\pi$, то есть:

$$\frac{11\pi }{6}<a_2<2\pi \mathrm{.}$$

2) На числовой окружности:

Поскольку окружность периодична, интервал для значений $t$ будет:

$$-\frac{\pi }{6}+2\pi n<t<\frac{7\pi }{6}+2\pi n\mathrm{.}$$

Ответ для части (б):

$$0<a_1<\frac{7\pi }{6}\mathrm{.}$$

в)

Интервал:

$$-\frac{3\pi }{4}+2\pi n<t<\frac{2\pi }{3}+2\pi n$$

1) На отрезке $0\le a\le 2\pi$:

Для интервала от $-\frac{3\pi }{4}$ до $\frac{2\pi }{3}$, разделим его на два промежутка:

Значения $a_1$ лежат от $0$ до $\frac{2\pi }{3}$, то есть:

$$0<a_1<\frac{2\pi }{3}\mathrm{.}$$

Значения $a_2$ лежат от $\frac{5\pi }{4}$ до $2\pi$, то есть:

$$\frac{5\pi }{4}<a_2<2\pi \mathrm{.}$$

2) На числовой окружности:

Поскольку окружность периодична, интервал для значений $t$ будет:

$$-\frac{3\pi }{4}+2\pi n<t<\frac{2\pi }{3}+2\pi n\mathrm{.}$$

Ответ для части (в):

$$\frac{\pi }{2}<a<\frac{3\pi }{2};$$

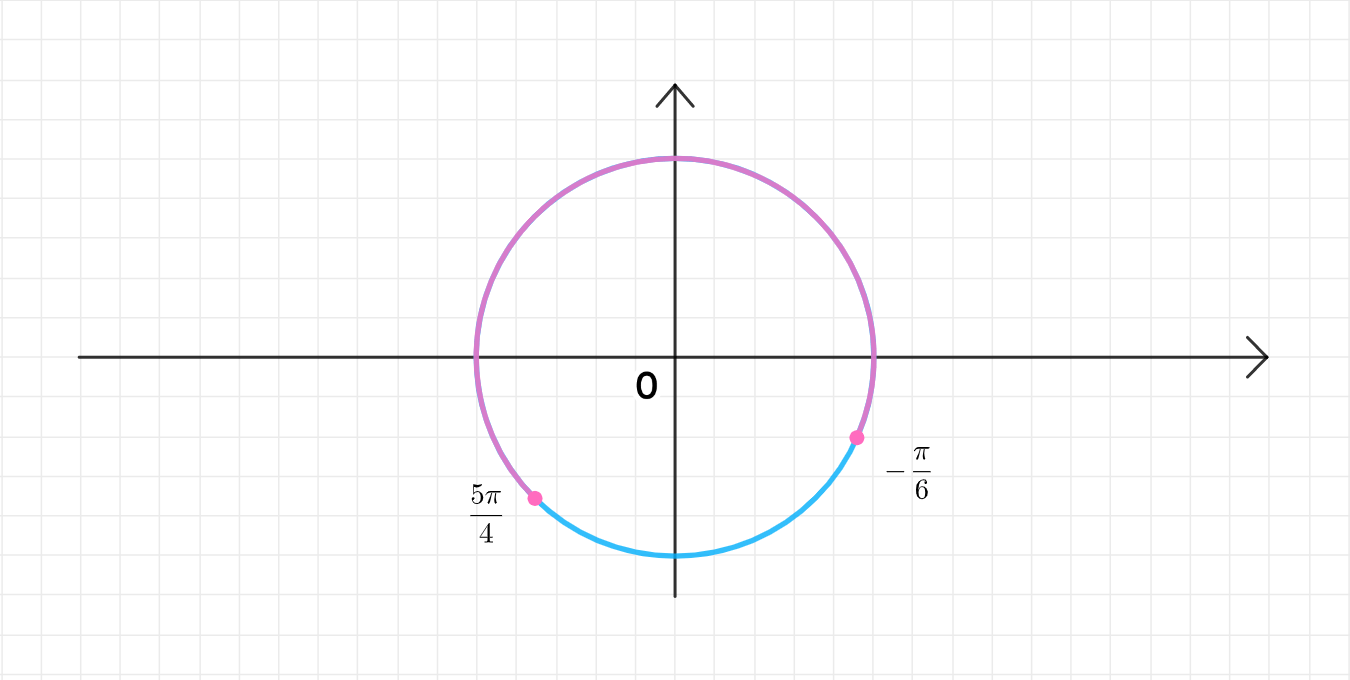
г)

Интервал:

$$-\frac{\pi }{6}+2\pi n<t<\frac{5\pi }{4}+2\pi n$$

1) На отрезке $0\le a\le 2\pi$:

Для интервала от $-\frac{\pi }{6}$ до $\frac{5\pi }{4}$, мы видим, что этот интервал проходит через начало окружности, то есть он будет разбиен на два промежутка:

Значения $a_1$ лежат от $0$ до $\frac{5\pi }{4}$, то есть:

$$0<a_1<\frac{5\pi }{4}\mathrm{.}$$

Значения $a_2$ лежат от $\frac{11\pi }{6}$ до $2\pi$, то есть:

$$\frac{11\pi }{6}<a_2<2\pi \mathrm{.}$$

2) На числовой окружности:

Поскольку окружность периодична, интервал для значений $t$ будет:

$$-\frac{\pi }{6}+2\pi n<t<\frac{5\pi }{4}+2\pi n\mathrm{.}$$

Ответ для части (г):

$$0<a_1<\frac{5\pi }{4};$$

Итоговые ответы:

а) $-\frac{\pi }{3}+2\pi n<t<\frac{\pi }{3}+2\pi n$

б) $0<a_1<\frac{7\pi }{6}$

в) $\frac{\pi }{2}<a<\frac{3\pi }{2}$

г) $0<a_1<\frac{5\pi }{4}$