ГДЗ по Алгебре 10 Класс Номер 11.3 Профильный Уровень Мордкович — Подробные Ответы

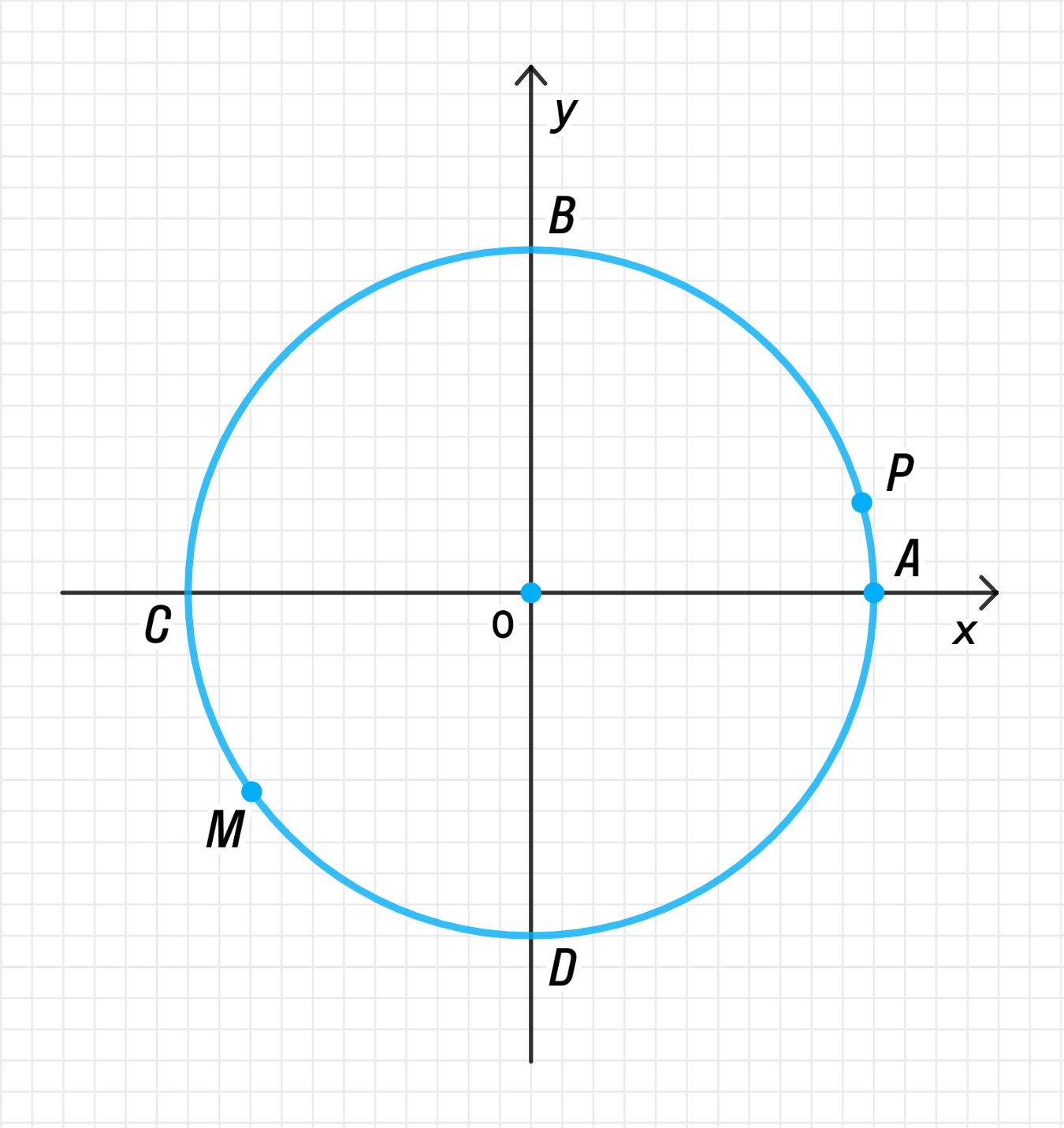
Третья четверть разделена точкой M в отношении 2 : 3, первая — точкой P в отношении 1 : 5. Найдите длину дуги:

а) CM;

б) AP;

в) PM;

г) MP.

Третья четверть разделена точкой $M$ в отношении 2:3, а первая — точкой $P$ в отношении 1:5 :

а) Длина дуги $CM$:

$$CM = 2 \cdot \frac{CD}{2+3} = CD \cdot \frac{2}{5} = \frac{\pi}{2} \cdot \frac{2}{5} = \frac{\pi}{5};$$

Ответ: $\frac{\pi}{5}$.

б) Длина дуги $AP$:

$$AP = 1 \cdot \frac{AB}{1+5} = AB \cdot \frac{1}{6} = \frac{\pi}{2} \cdot \frac{1}{6} = \frac{\pi}{12};$$

Ответ: $\frac{\pi}{12}$.

в) Длина дуги $PM$:

$$PB = 5 \cdot \frac{AB}{1+5} = AB \cdot \frac{5}{6} = \frac{\pi}{2} \cdot \frac{5}{6} = \frac{5\pi}{12};$$ $$CM = 2 \cdot \frac{CD}{2+3} = CD \cdot \frac{2}{5} = \frac{\pi}{2} \cdot \frac{2}{5} = \frac{\pi}{5};$$ $$PM = PB + BC + CM = \frac{5\pi}{12} + \frac{\pi}{2} + \frac{\pi}{5} = \frac{25\pi + 30\pi + 12\pi}{60} = \frac{67\pi}{60};$$

Ответ: $\frac{67\pi}{60}$.

г) Длина дуги $MP$:

$$MD = 3 \cdot \frac{CD}{2+3} = CD \cdot \frac{3}{5} = \frac{\pi}{2} \cdot \frac{3}{5} = \frac{3\pi}{10};$$ $$AP = 1 \cdot \frac{AB}{1+5} = AB \cdot \frac{1}{6} = \frac{\pi}{2} \cdot \frac{1}{6} = \frac{\pi}{12};$$ $$MP = MD + DA + AP = \frac{3\pi}{10} + \frac{\pi}{2} + \frac{\pi}{12} = \frac{18\pi + 30\pi + 5\pi}{60} = \frac{53\pi}{60};$$

Ответ: $\frac{53\pi}{60}$.

У нас есть окружность с длиной дуги, для которой требуется найти длины нескольких отрезков. Окружность разделена на несколько частей точками $M$ и $P$, причем точка $M$ делит третью четверть в отношении 2:3, а точка $P$ делит первую четверть в отношении 1:5. Для каждой из этих дуг нужно найти их длины.

Мы будем работать с несколькими формулами для вычисления длин дуг окружности:

Длина дуги окружности вычисляется по формуле:

$$L = \theta \cdot r,$$

где $\theta$ — центральный угол, соответствующий дуге, а $r$ — радиус окружности. Однако, так как радиус не задан, для нас будет важна только пропорциональная длина дуги относительно углов, выраженная через $\pi$ (половина окружности — это $\frac{\pi}{2}$, целая — $\pi$).

Пропорциональная длина дуги:
Так как вся окружность имеет длину $\pi$, нам нужно будет вычислить долю окружности, которую занимают рассматриваемые дуги.

а) Длина дуги $CM$:

Точка $M$ делит третью четверть окружности в отношении 2:3. Это означает, что $M$ делит третью четверть так, что длина дуги $CM$ составляет 2/5 от общей длины третьей четверти, а оставшаяся часть (дуга $MB$) составляет 3/5 от длины третьей четверти.

Общая длина третьей четверти окружности — это $\frac{\pi}{2}$, поскольку третья четверть составляет 90 градусов, то есть $\frac{90^\circ}{360^\circ} = \frac{1}{4}$ от полной окружности.

Теперь найдем длину дуги $CM$, которая будет составлять 2/5 от $\frac{\pi}{2}$:

$$CM = 2 \cdot \frac{CD}{2+3} = CD \cdot \frac{2}{5}.$$

Подставляем $CD = \frac{\pi}{2}$:

$$CM = \frac{\pi}{2} \cdot \frac{2}{5} = \frac{\pi}{5}.$$

Ответ: $\frac{\pi}{5}$.

б) Длина дуги $AP$:

Точка $P$ делит первую четверть окружности в отношении 1:5. Это означает, что длина дуги $AP$ составляет 1/6 от общей длины первой четверти, а оставшаяся часть (дуга $PB$) составляет 5/6 от длины первой четверти.

Общая длина первой четверти окружности — это также $\frac{\pi}{2}$, так как первая четверть также составляет 90 градусов, то есть $\frac{90^\circ}{360^\circ} = \frac{1}{4}$ от полной окружности.

Найдем длину дуги $AP$, которая составляет 1/6 от $\frac{\pi}{2}$:

$$AP = 1 \cdot \frac{AB}{1+5} = AB \cdot \frac{1}{6}.$$

Подставляем $AB = \frac{\pi}{2}$:

$$AP = \frac{\pi}{2} \cdot \frac{1}{6} = \frac{\pi}{12}.$$

Ответ: $\frac{\pi}{12}$.

в) Длина дуги $PM$:

Дуга $PM$ состоит из суммы трех дуг: $PB$, $BC$ и $CM$.

Для начала найдем длину дуги $PB$, которая составит 5/6 от длины первой четверти. Мы уже вычислили длину первой четверти, равную $\frac{\pi}{2}$, так что:

$$PB = 5 \cdot \frac{AB}{1+5} = AB \cdot \frac{5}{6}.$$

Подставляем $AB = \frac{\pi}{2}$:

$$PB = \frac{\pi}{2} \cdot \frac{5}{6} = \frac{5\pi}{12}.$$

Теперь вычислим длину дуги $BC$, которая равна длине оставшейся части третьей четверти, то есть $\frac{\pi}{2}$, минус длина дуги $CM$, которую мы нашли ранее:

$$BC = \frac{\pi}{2} — \frac{\pi}{5}.$$

Для приведения к общему знаменателю:

$$BC = \frac{5\pi}{10} — \frac{2\pi}{10} = \frac{3\pi}{10}.$$

Теперь мы можем вычислить длину дуги $PM$:

$$PM = PB + BC + CM = \frac{5\pi}{12} + \frac{3\pi}{10} + \frac{\pi}{5}.$$

Приводим к общему знаменателю (60):

$$PM = \frac{5\pi}{12} + \frac{3\pi}{10} + \frac{\pi}{5} = \frac{25\pi}{60} + \frac{18\pi}{60} + \frac{12\pi}{60} = \frac{67\pi}{60}.$$

Ответ: $\frac{67\pi}{60}$.

г) Длина дуги $MP$:

Дуга $MP$ состоит из суммы дуг $MD$, $DA$ и $AP$.

Для начала найдем длину дуги $MD$, которая составляет 3/5 от длины третьей четверти:

$$MD = 3 \cdot \frac{CD}{2+3} = CD \cdot \frac{3}{5}.$$

Подставляем $CD = \frac{\pi}{2}$:

$$MD = \frac{\pi}{2} \cdot \frac{3}{5} = \frac{3\pi}{10}.$$

Длина дуги $DA$ — это оставшаяся часть второй четверти, которая составляет $\frac{\pi}{2}$, и она должна быть учтена.

Теперь вычислим длину дуги $MP$:

$$MP = MD + DA + AP = \frac{3\pi}{10} + \frac{\pi}{2} + \frac{\pi}{12}.$$

Приводим к общему знаменателю (60):

$$MP = \frac{3\pi}{10} + \frac{\pi}{2} + \frac{\pi}{12} = \frac{18\pi}{60} + \frac{30\pi}{60} + \frac{5\pi}{60} = \frac{53\pi}{60}.$$

Ответ: $\frac{53\pi}{60}$.