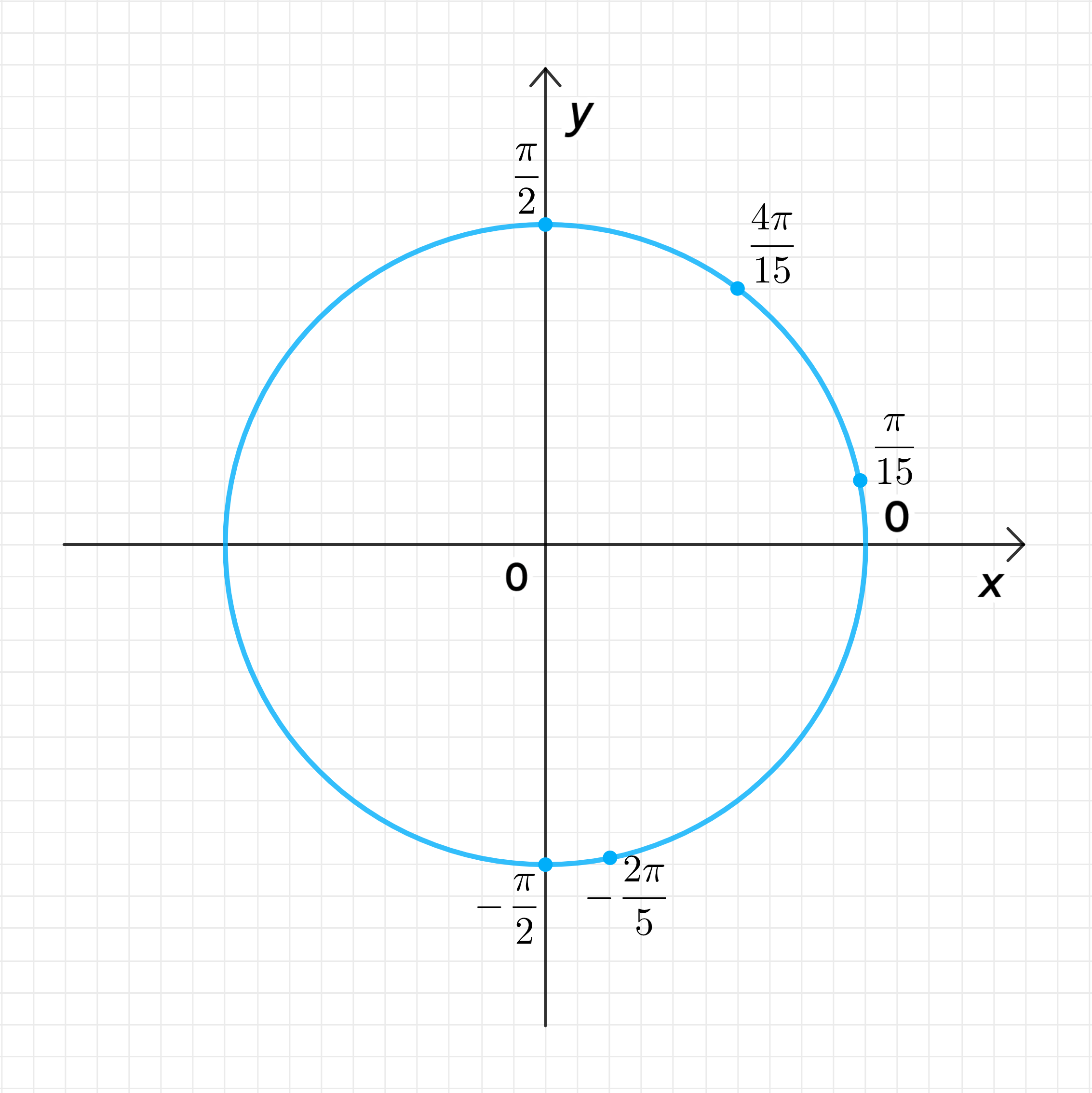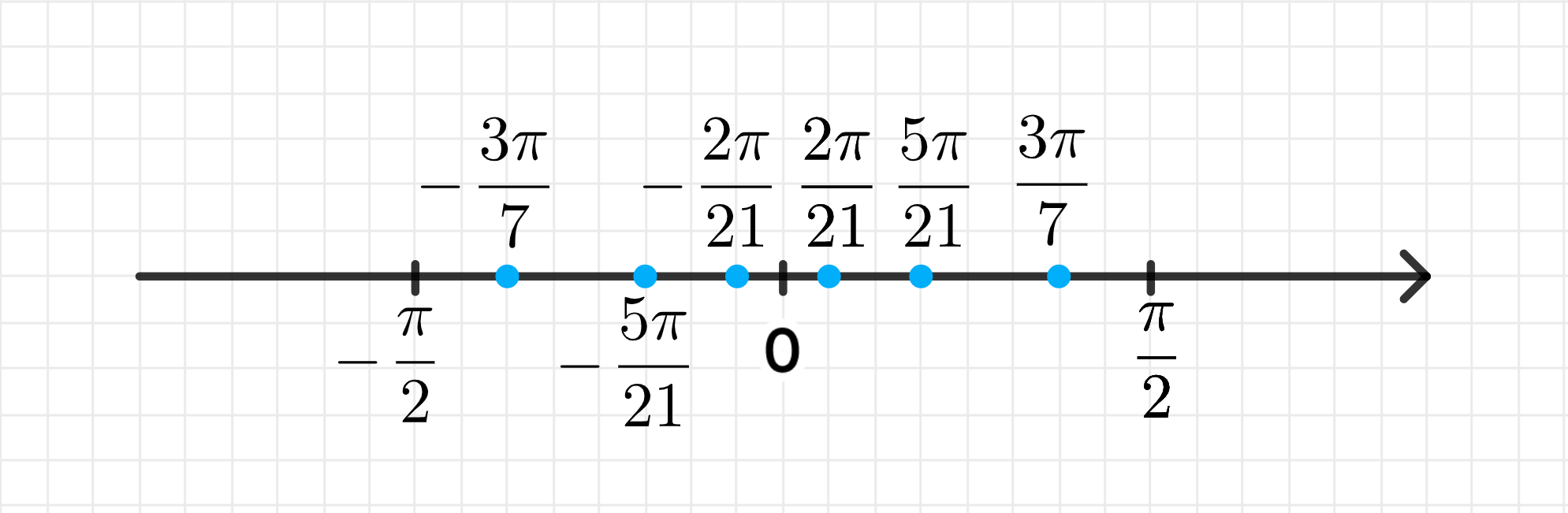ГДЗ по Алгебре 10 Класс Номер 11.32 Профильный Уровень Мордкович — Подробные Ответы

На числовой прямой и числовой окружности отметьте все точки $M(t)$, заданные формулой и принадлежащие отрезку $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$:

$t = (-1)^n \cdot \frac{\pi}{15} + \frac{\pi n}{3}$

$t = \pm \frac{\pi}{8} + \frac{\pi n}{4}$

$t = (-1)^{n+1} \cdot \frac{\pi}{8} + \frac{\pi n}{4}$

$t = \pm \frac{3\pi}{7} + \frac{\pi n}{3}$

На числовой окружности и числовой прямой отметим все точки $M(t)$, заданные формулой и принадлежащие отрезку $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$.

а) $t = (-1)^n \cdot \frac{\pi}{15} + \frac{\pi n}{3}$

Значения чисел:

$$t(-2) = (-1)^{-2} \cdot \frac{\pi}{15} — \frac{2\pi}{3} = \frac{\pi}{15} — \frac{2\pi}{3} = -\frac{3\pi}{5} < -\frac{\pi}{2};$$ $$t(-1) = (-1)^{-1} \cdot \frac{\pi}{15} — \frac{\pi}{3} = -\frac{\pi}{15} — \frac{\pi}{3} = -\frac{6\pi}{15} = -\frac{2\pi}{5};$$ $$t(0) = (-1)^0 \cdot \frac{\pi}{15} = \frac{\pi}{15};$$ $$t(1) = (-1)^1 \cdot \frac{\pi}{15} + \frac{\pi}{3} = -\frac{\pi}{15} + \frac{\pi}{3} = \frac{4\pi}{15};$$ $$t(2) = (-1)^2 \cdot \frac{\pi}{15} + \frac{2\pi}{3} = \frac{\pi}{15} + \frac{2\pi}{3} = \frac{11\pi}{15} > \frac{\pi}{2};$$

На числовой окружности:

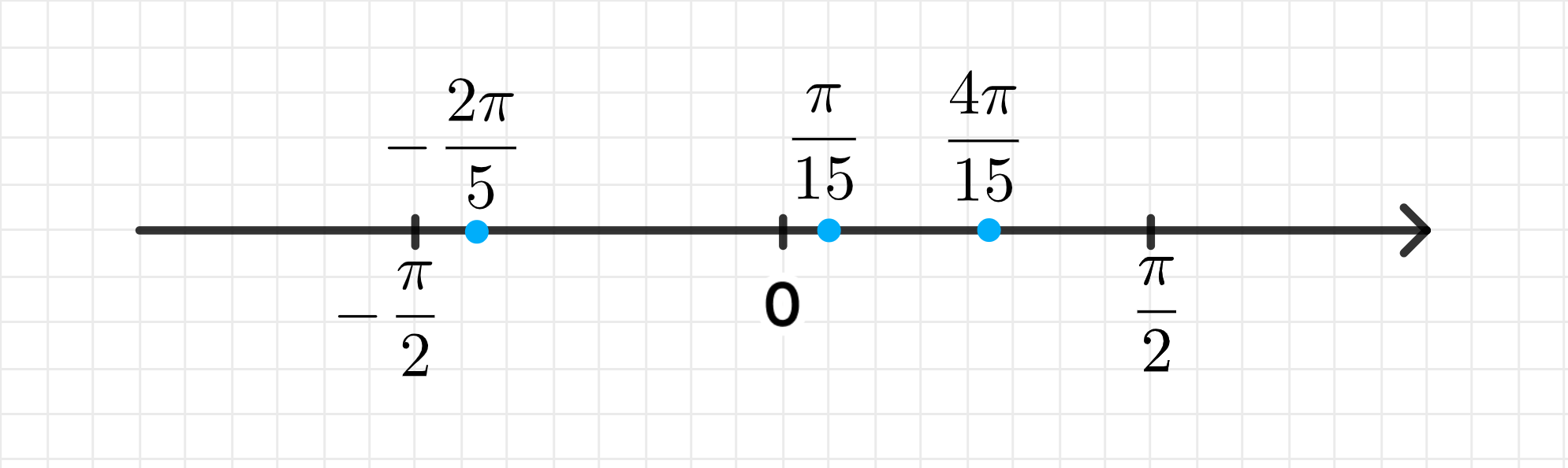
На числовой прямой:

Ответ: $-\frac{2\pi}{5}; \frac{\pi}{15}; \frac{4\pi}{15}$.

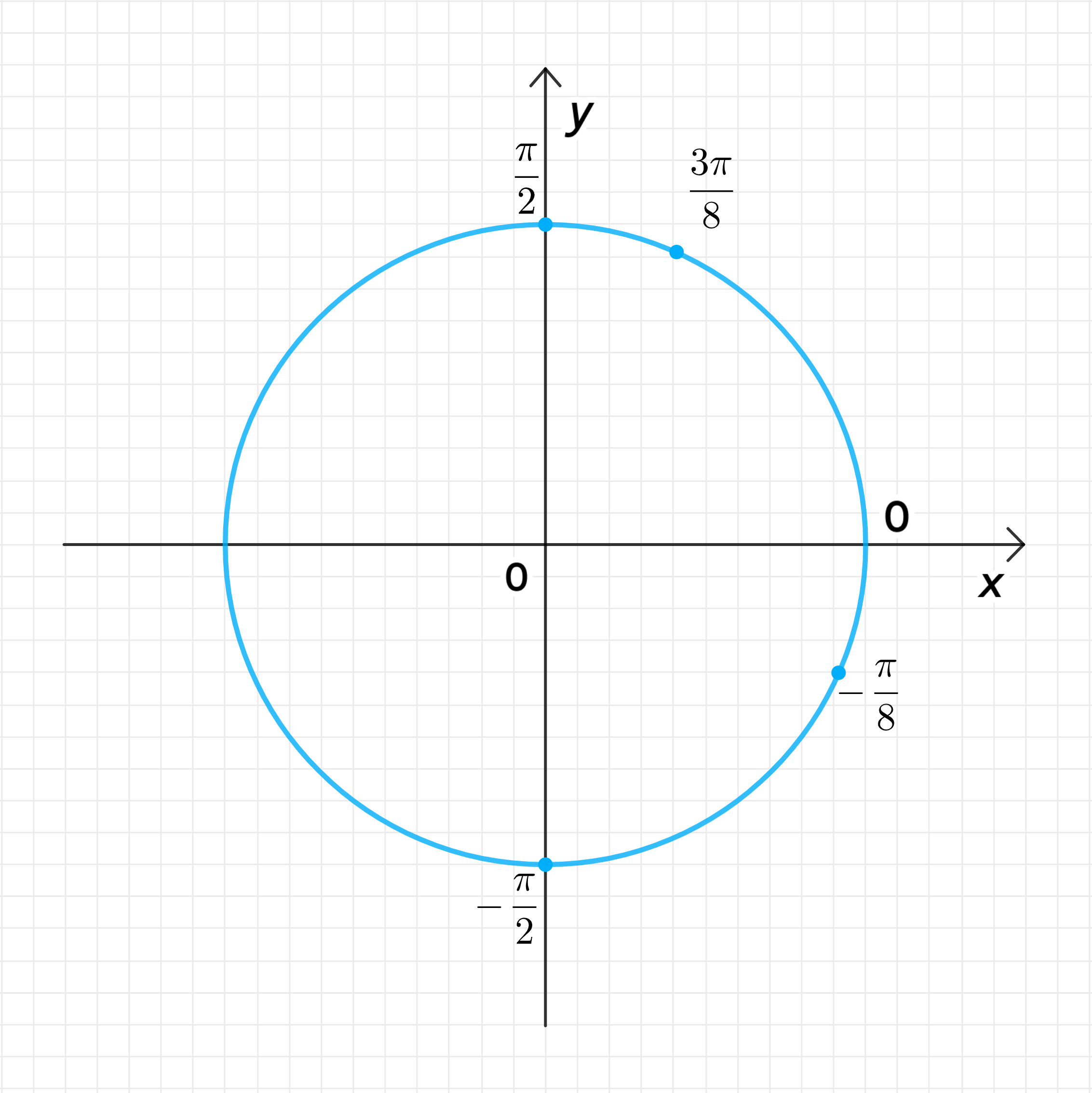
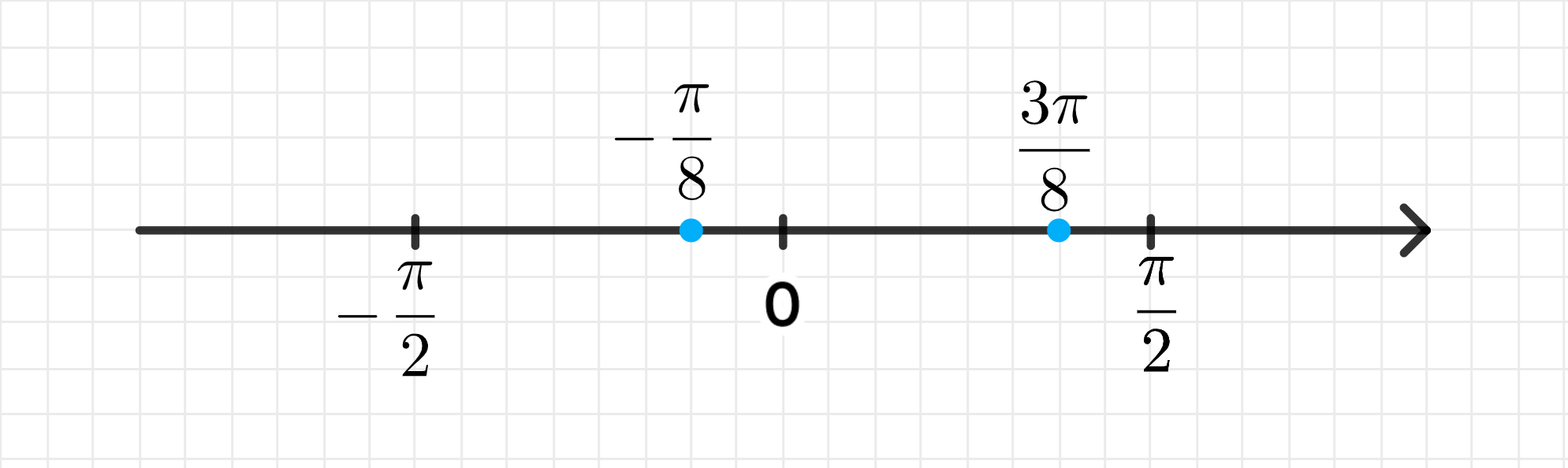
б) $t = \pm \frac{\pi}{8} + \frac{\pi n}{4}$

Значения чисел:

$$t(-2) = -\frac{\pi}{8} — \frac{2\pi}{4} = -\frac{5\pi}{8} < -\frac{\pi}{2};$$ $$t(-2) = +\frac{\pi}{8} — \frac{2\pi}{4} = -\frac{3\pi}{8};$$ $$t(-1) = -\frac{\pi}{8} — \frac{\pi}{4} = -\frac{3\pi}{8};$$ $$t(-1) = +\frac{\pi}{8} — \frac{\pi}{4} = -\frac{\pi}{8};$$ $$t(0) = \pm \frac{\pi}{8};$$ $$t(1) = -\frac{\pi}{8} + \frac{\pi}{4} = \frac{\pi}{8};$$ $$t(1) = +\frac{\pi}{8} + \frac{\pi}{4} = \frac{3\pi}{8};$$ $$t(2) = -\frac{\pi}{8} + \frac{2\pi}{4} = \frac{3\pi}{8};$$ $$t(2) = +\frac{\pi}{8} + \frac{2\pi}{4} = \frac{5\pi}{8} > \frac{\pi}{2};$$

На числовой окружности:

На числовой прямой:

Ответ: $\pm \frac{\pi}{8}; \pm \frac{3\pi}{8}$.

в) $t = (-1)^{n+1} \cdot \frac{\pi}{8} + \frac{\pi n}{4}$

Значения чисел:

$$t(-2) = (-1)^{-1} \cdot \frac{\pi}{8} — \frac{2\pi}{4} = -\frac{\pi}{8} — \frac{4\pi}{8} = -\frac{5\pi}{8} < -\frac{\pi}{2};$$ $$t(-1) = (-1)^0 \cdot \frac{\pi}{8} — \frac{\pi}{4} = \frac{\pi}{8} — \frac{\pi}{4} = -\frac{\pi}{8};$$ $$t(0) = (-1)^1 \cdot \frac{\pi}{8} = -\frac{\pi}{8};$$ $$t(1) = (-1)^2 \cdot \frac{\pi}{8} + \frac{\pi}{4} = \frac{\pi}{8} + \frac{2\pi}{8} = \frac{3\pi}{8};$$ $$t(2) = (-1)^3 \cdot \frac{\pi}{8} + \frac{2\pi}{4} = -\frac{\pi}{8} + \frac{4\pi}{8} = \frac{3\pi}{8};$$ $$t(3) = (-1)^4 \cdot \frac{\pi}{8} + \frac{3\pi}{4} = \frac{\pi}{8} + \frac{6\pi}{8} = \frac{7\pi}{8} > \frac{\pi}{2};$$

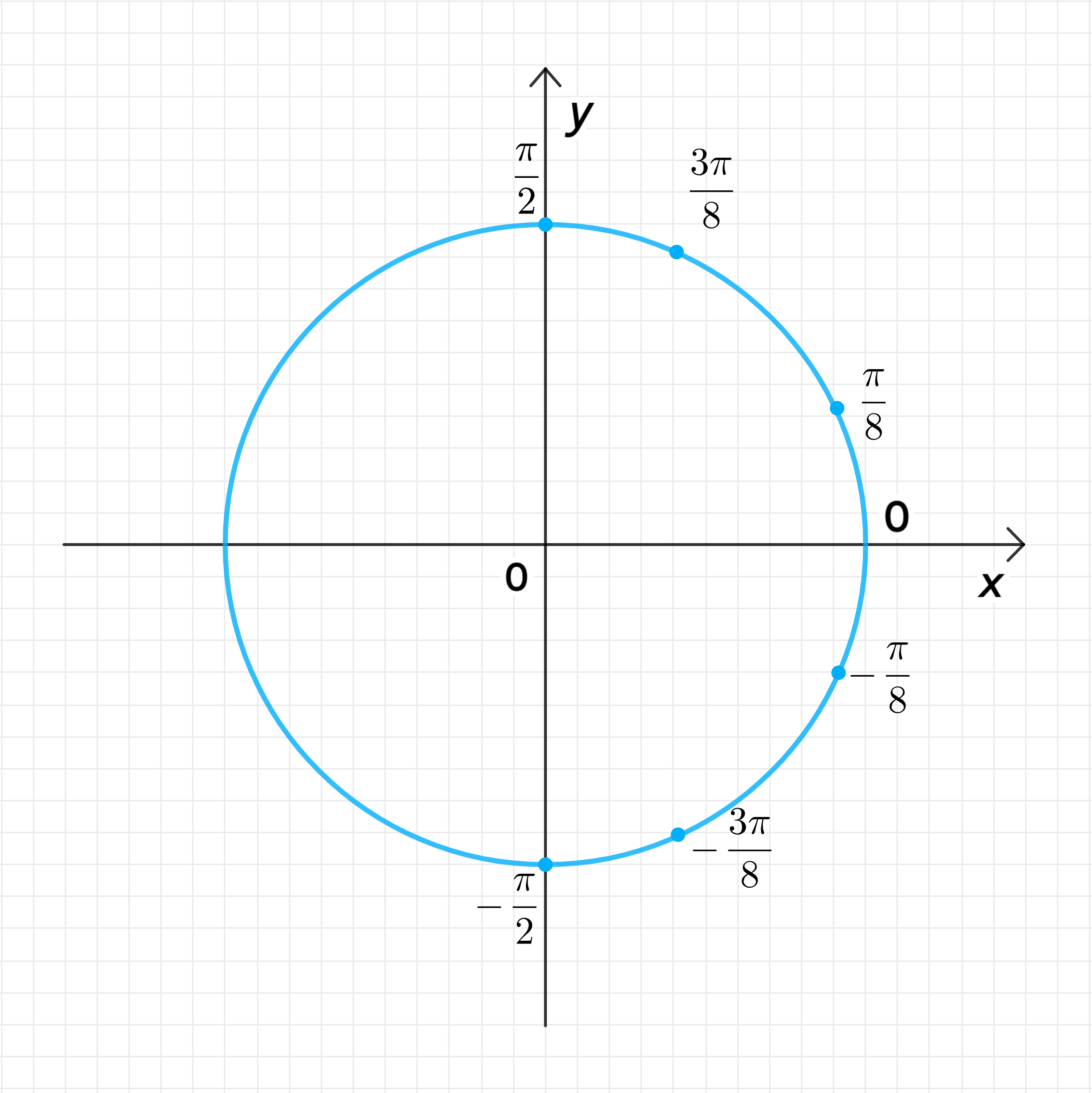
На числовой окружности:

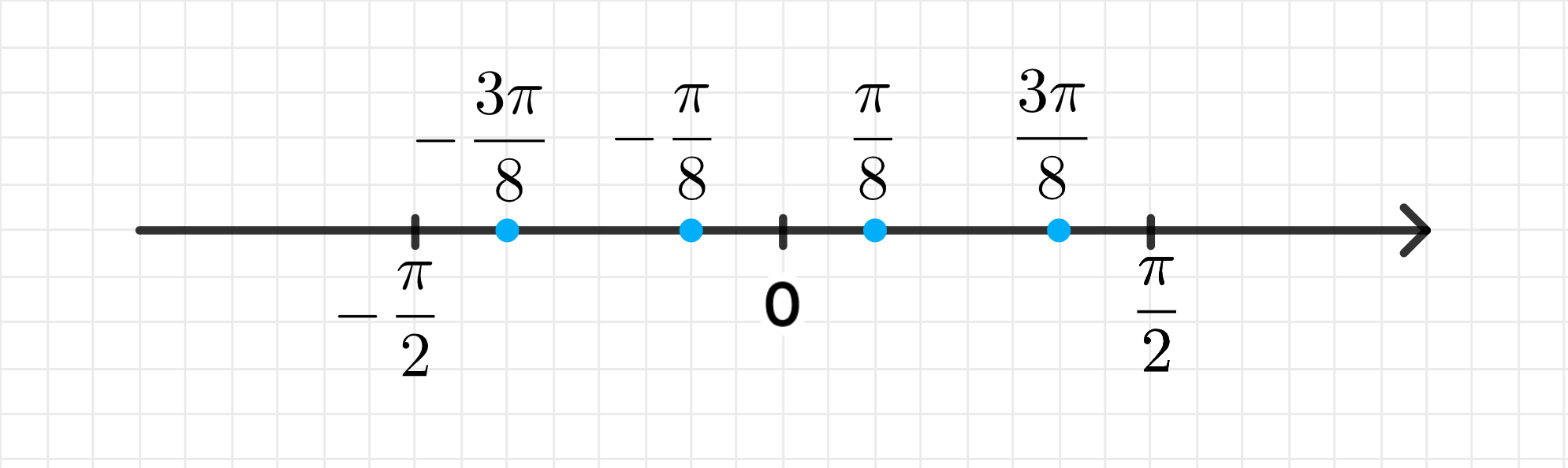
На числовой прямой:

Ответ: $-\frac{\pi}{8}; \frac{3\pi}{8}$.

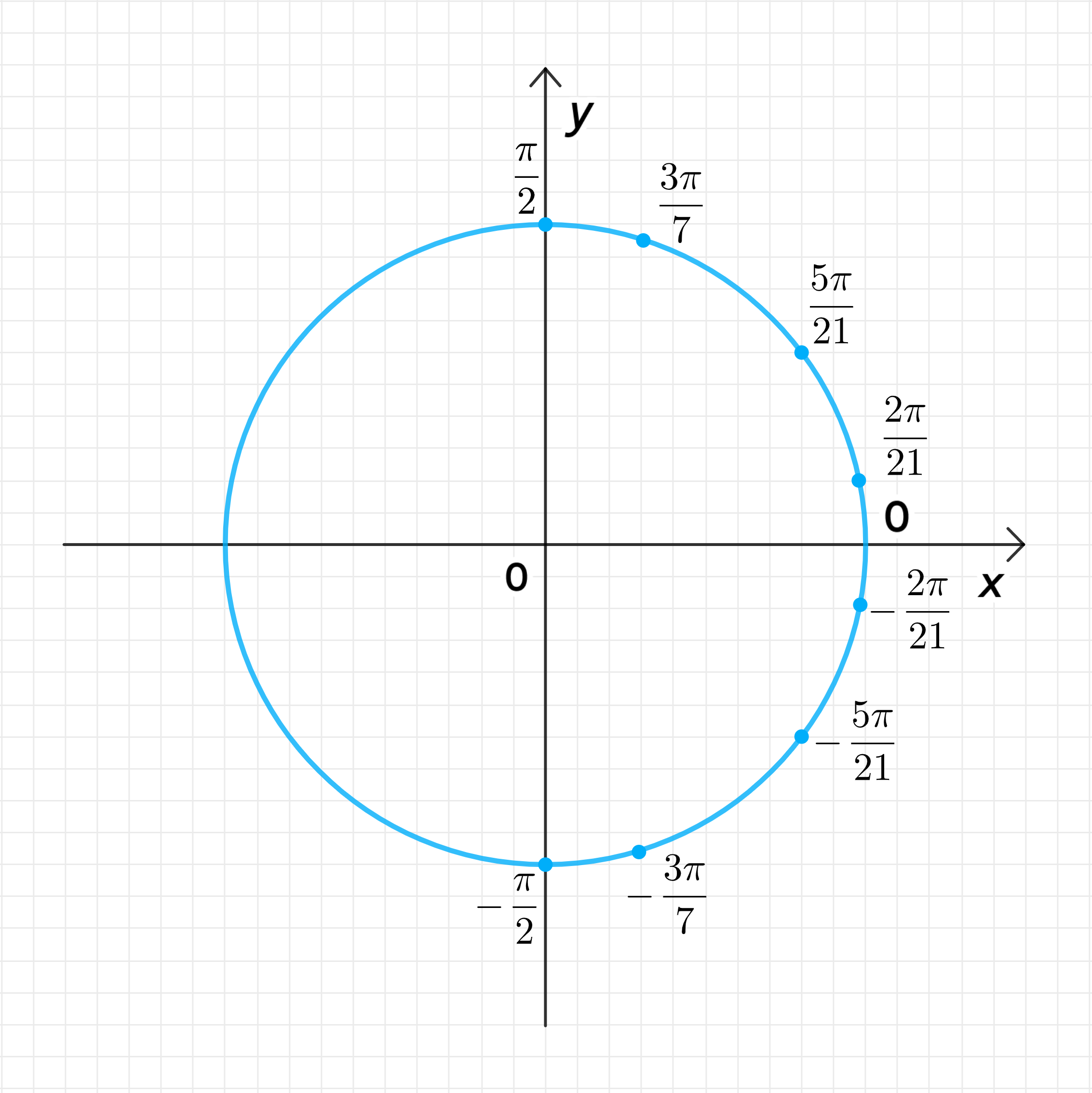
г) $t = \pm \frac{3\pi}{7} + \frac{\pi n}{3}$

Значения чисел:

$$t(-1) = -\frac{3\pi}{7} — \frac{\pi}{3} = -\frac{16\pi}{21} < -\frac{\pi}{2};$$ $$t(-2) = +\frac{3\pi}{7} — \frac{2\pi}{3} = -\frac{5\pi}{21};$$ $$t(0) = \pm \frac{3\pi}{7};$$ $$t(1) = -\frac{3\pi}{7} + \frac{\pi}{3} = -\frac{2\pi}{21};$$ $$t(1) = +\frac{3\pi}{7} + \frac{\pi}{3} = \frac{16\pi}{21} > \frac{\pi}{2};$$ $$t(2) = -\frac{3\pi}{7} + \frac{2\pi}{3} = \frac{5\pi}{21};$$

На числовой окружности:

На числовой прямой:

Ответ: $\pm \frac{3\pi}{7}; \pm \frac{2\pi}{21}; \pm \frac{5\pi}{21}$.

На числовой окружности и числовой прямой отметим все точки $M(t)$, заданные формулой и принадлежащие отрезку $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$.

а) $t = (-1)^n \cdot \frac{\pi}{15} + \frac{\pi n}{3}$

Шаг 1: Вычисление значений для различных $n$.

Подставляем разные значения для $n$ и вычисляем $t$.

Для $n = -2$:

$$t(-2) = (-1)^{-2} \cdot \frac{\pi}{15} — \frac{2\pi}{3} = \frac{\pi}{15} — \frac{2\pi}{3} = \frac{\pi}{15} — \frac{10\pi}{15} = -\frac{9\pi}{15} = -\frac{3\pi}{5}.$$

Так как $-\frac{3\pi}{5} < -\frac{\pi}{2}$, точка не принадлежит отрезку.

Для $n = -1$:

$$t(-1) = (-1)^{-1} \cdot \frac{\pi}{15} — \frac{\pi}{3} = -\frac{\pi}{15} — \frac{\pi}{3} = -\frac{\pi}{15} — \frac{5\pi}{15} = -\frac{6\pi}{15} = -\frac{2\pi}{5}.$$

Так как $-\frac{2\pi}{5} > -\frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 0$:

$$t(0) = (-1)^0 \cdot \frac{\pi}{15} + \frac{\pi \cdot 0}{3} = \frac{\pi}{15}.$$

Так как $\frac{\pi}{15} > -\frac{\pi}{2}$ и $\frac{\pi}{15} < \frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 1$:

$$t(1) = (-1)^1 \cdot \frac{\pi}{15} + \frac{\pi}{3} = -\frac{\pi}{15} + \frac{\pi}{3} = -\frac{\pi}{15} + \frac{5\pi}{15} = \frac{4\pi}{15}.$$

Так как $\frac{4\pi}{15} < \frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 2$:

$$t(2) = (-1)^2 \cdot \frac{\pi}{15} + \frac{2\pi}{3} = \frac{\pi}{15} + \frac{2\pi}{3} = \frac{\pi}{15} + \frac{10\pi}{15} = \frac{11\pi}{15}.$$

Так как $\frac{11\pi}{15} > \frac{\pi}{2}$, точка не принадлежит отрезку.

Шаг 2: Ответ для числовой окружности и прямой.

Ответ для значений на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$:

$$-\frac{2\pi}{5}; \frac{\pi}{15}; \frac{4\pi}{15}.$$

б) $t = \pm \frac{\pi}{8} + \frac{\pi n}{4}$

Шаг 1: Вычисление значений для различных $n$.

Подставляем разные значения для $n$ и вычисляем $t$.

Для $n = -2$:

$$t(-2) = -\frac{\pi}{8} — \frac{2\pi}{4} = -\frac{\pi}{8} — \frac{\pi}{2} = -\frac{\pi}{8} — \frac{4\pi}{8} = -\frac{5\pi}{8}.$$

Так как $-\frac{5\pi}{8} < -\frac{\pi}{2}$, точка не принадлежит отрезку.

Для $n = -1$:

$$t(-1) = -\frac{\pi}{8} — \frac{\pi}{4} = -\frac{\pi}{8} — \frac{2\pi}{8} = -\frac{3\pi}{8}.$$

Так как $-\frac{3\pi}{8} > -\frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 0$:

$$t(0) = \pm \frac{\pi}{8}.$$

Так как $\frac{\pi}{8} < \frac{\pi}{2}$, обе точки принадлежат отрезку.

Для $n = 1$:

$$t(1) = -\frac{\pi}{8} + \frac{\pi}{4} = \frac{\pi}{8};$$ $$t(1) = +\frac{\pi}{8} + \frac{\pi}{4} = \frac{3\pi}{8}.$$

Так как $\frac{3\pi}{8} < \frac{\pi}{2}$, обе точки принадлежат отрезку.

Для $n = 2$:

$$t(2) = -\frac{\pi}{8} + \frac{2\pi}{4} = \frac{3\pi}{8};$$ $$t(2) = +\frac{\pi}{8} + \frac{2\pi}{4} = \frac{5\pi}{8}.$$

Так как $\frac{5\pi}{8} > \frac{\pi}{2}$, вторая точка не принадлежит отрезку.

Шаг 2: Ответ для числовой окружности и прямой.

Ответ для значений на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$:

$$\pm \frac{\pi}{8}; \pm \frac{3\pi}{8}.$$

в) $t = (-1)^{n+1} \cdot \frac{\pi}{8} + \frac{\pi n}{4}$

Шаг 1: Вычисление значений для различных $n$.

Подставляем разные значения для $n$ и вычисляем $t$.

Для $n = -2$:

$$t(-2) = (-1)^{-1} \cdot \frac{\pi}{8} — \frac{2\pi}{4} = -\frac{\pi}{8} — \frac{4\pi}{8} = -\frac{5\pi}{8}.$$

Так как $-\frac{5\pi}{8} < -\frac{\pi}{2}$, точка не принадлежит отрезку.

Для $n = -1$:

$$t(-1) = (-1)^0 \cdot \frac{\pi}{8} — \frac{\pi}{4} = \frac{\pi}{8} — \frac{\pi}{4} = -\frac{\pi}{8}.$$

Так как $-\frac{\pi}{8} > -\frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 0$:

$$t(0) = (-1)^1 \cdot \frac{\pi}{8} = -\frac{\pi}{8}.$$

Так как $-\frac{\pi}{8} > -\frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 1$:

$$t(1) = (-1)^2 \cdot \frac{\pi}{8} + \frac{\pi}{4} = \frac{\pi}{8} + \frac{2\pi}{8} = \frac{3\pi}{8}.$$

Так как $\frac{3\pi}{8} < \frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 2$:

$$t(2) = (-1)^3 \cdot \frac{\pi}{8} + \frac{2\pi}{4} = -\frac{\pi}{8} + \frac{4\pi}{8} = \frac{3\pi}{8}.$$

Так как $\frac{3\pi}{8} < \frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 3$:

$$t(3) = (-1)^4 \cdot \frac{\pi}{8} + \frac{3\pi}{4} = \frac{\pi}{8} + \frac{6\pi}{8} = \frac{7\pi}{8}.$$

Так как $\frac{7\pi}{8} > \frac{\pi}{2}$, точка не принадлежит отрезку.

Шаг 2: Ответ для числовой окружности и прямой.

Ответ для значений на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$:

$$-\frac{\pi}{8}; \frac{3\pi}{8}.$$

г) $t = \pm \frac{3\pi}{7} + \frac{\pi n}{3}$

Шаг 1: Вычисление значений для различных $n$.

Подставляем разные значения для $n$ и вычисляем $t$.

Для $n = -1$:

$$t(-1) = -\frac{3\pi}{7} — \frac{\pi}{3} = -\frac{9\pi}{21} — \frac{7\pi}{21} = -\frac{16\pi}{21}.$$

Так как $-\frac{16\pi}{21} < -\frac{\pi}{2}$, точка не принадлежит отрезку.

Для $n = -2$:

$$t(-2) = +\frac{3\pi}{7} — \frac{2\pi}{3} = -\frac{5\pi}{21}.$$

Так как $-\frac{5\pi}{21} < -\frac{\pi}{2}$, точка не принадлежит отрезку.

Для $n = 0$:

$$t(0) = \pm \frac{3\pi}{7}.$$

Так как $\frac{3\pi}{7} < \frac{\pi}{2}$, точка принадлежит отрезку.

Для $n = 1$:

$$t(1) = -\frac{3\pi}{7} + \frac{\pi}{3} = -\frac{2\pi}{21};$$ $$t(1) = +\frac{3\pi}{7} + \frac{\pi}{3} = \frac{16\pi}{21}.$$

Так как $\frac{16\pi}{21} > \frac{\pi}{2}$, вторая точка не принадлежит отрезку.

Для $n = 2$:

$$t(2) = -\frac{3\pi}{7} + \frac{2\pi}{3} = \frac{5\pi}{21}.$$

Так как $\frac{5\pi}{21} < \frac{\pi}{2}$, точка принадлежит отрезку.

Шаг 2: Ответ для числовой окружности и прямой.

Ответ для значений на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$:

$$\pm \frac{3\pi}{7}; \pm \frac{2\pi}{21}; \pm \frac{5\pi}{21}.$$