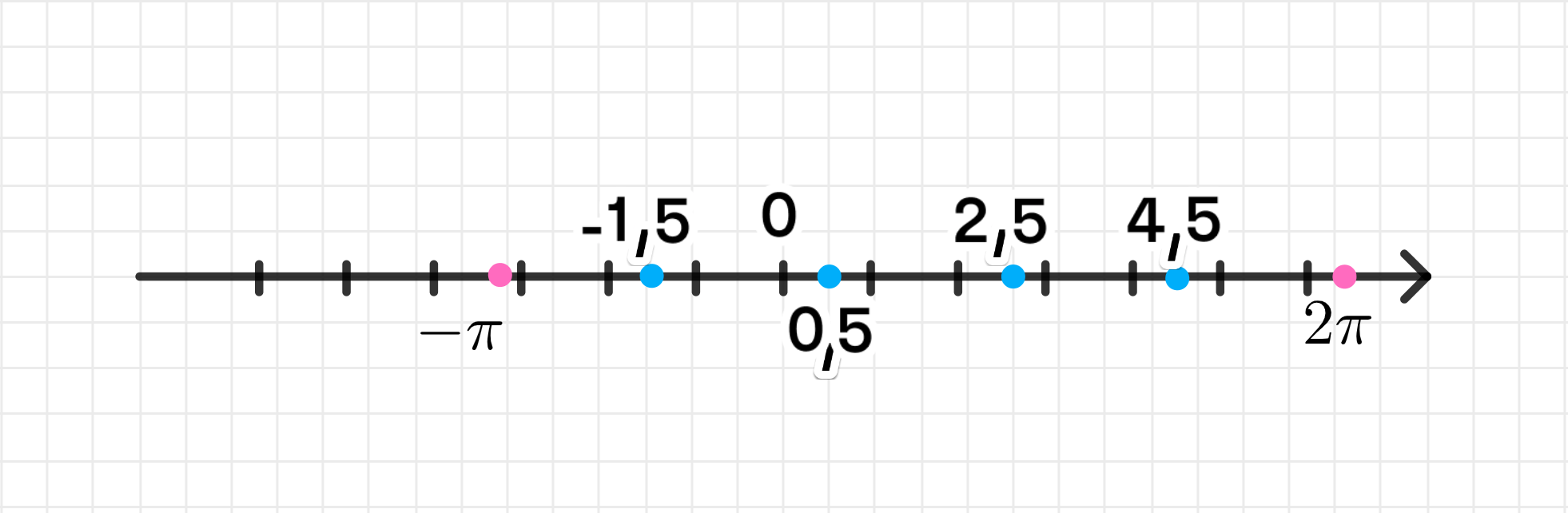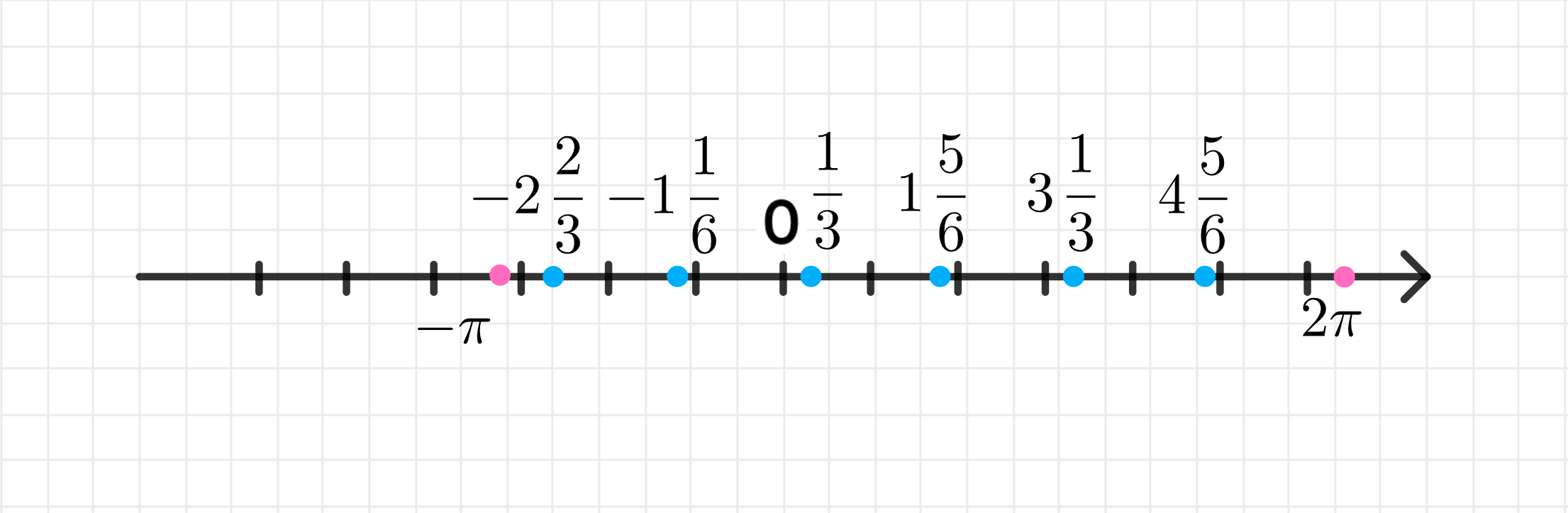ГДЗ по Алгебре 10 Класс Номер 11.34 Профильный Уровень Мордкович — Подробные Ответы

На числовой прямой и числовой окружности отметьте все точки $M(t)$, заданные формулой и принадлежащие отрезку $[-π; 2π]$:

$t = n$

$t = \frac{1}{2} + 2n$

$t = 2n + 1$

$t = \frac{1}{3} + \frac{3n}{2}$

На числовой окружности и числовой прямой отметить все точки $M(t)$, заданные формулой и принадлежащие отрезку $[-π; 2π]$.

а) $t = n$

Значения чисел:

$$t(-4) = -4 < -π;$$ $$t(7) = 7 > 2π;$$ $$-3 \leq t \leq 6;$$

На числовой окружности:

На числовой прямой:

Ответ: $-3; -2; -1; 0; 1; 2; 3; 4; 5; 6.$

б) $t = \frac{1}{2} + 2n$

Значения чисел:

$$t(-2) = \frac{1}{2} — 4 = -3,5 < -π;$$ $$t(-1) = \frac{1}{2} — 2 = -1,5;$$ $$t(0) = \frac{1}{2} = 0,5;$$ $$t(1) = \frac{1}{2} + 2 = 2,5;$$ $$t(2) = \frac{1}{2} + 4 = 4,5;$$ $$t(3) = \frac{1}{2} + 6 = 6,5 > 2π;$$

На числовой окружности:

На числовой прямой:

Ответ: $-1,5; 0,5; 2,5; 4,5.$

в) $t = 2n + 1$

Значения чисел:

$$t(-3) = -6 + 1 = -5 < -π;$$ $$t(-2) = -4 + 1 = -3;$$ $$t(-1) = -2 + 1 = -1;$$ $$t(0) = 1;$$ $$t(1) = 2 + 1 = 3;$$ $$t(2) = 4 + 1 = 5;$$ $$t(3) = 6 + 1 = 7 > 2π;$$

На числовой окружности:

На числовой прямой:

Ответ: $-3; -1; 1; 3; 5.$

г) $t = \frac{1}{3} + \frac{3n}{2}$

Значения чисел:

$$t(-3) = \frac{1}{3} — \frac{9}{2} = -\frac{25}{6} = -4\frac{1}{6} < -π;$$ $$t(-2) = \frac{1}{3} — \frac{6}{2} = \frac{1}{3} — 3 = -2\frac{2}{3};$$ $$t(-1) = \frac{1}{3} — \frac{3}{2} = -\frac{7}{6} = -1\frac{1}{6};$$ $$t(0) = \frac{1}{3};$$ $$t(1) = \frac{1}{3} + \frac{3}{2} = \frac{11}{6} = 1\frac{5}{6};$$ $$t(2) = \frac{1}{3} + \frac{6}{2} = \frac{1}{3} + 3 = 3\frac{1}{3};$$ $$t(3) = \frac{1}{3} + \frac{9}{2} = \frac{29}{6} = 4\frac{5}{6};$$ $$t(4) = \frac{1}{3} + \frac{12}{2} = \frac{1}{3} + 6 = 6\frac{1}{3} > 2π;$$

На числовой окружности:

На числовой прямой:

Ответ: $-2\frac{2}{3}; -1\frac{1}{6}; \frac{1}{3}; 1\frac{5}{6}; 3\frac{1}{3}; 4\frac{5}{6}.$

На числовой окружности и числовой прямой отметить все точки $M(t)$, заданные формулой и принадлежащие отрезку $[-π; 2π]$.

а) $t = n$

Задание функции $t = n$

Здесь $t$ задается как целое число $n$. Это значит, что $t$ может принимать любые целые значения, например, $-3, -2, -1, 0, 1, 2, 3, \dots$. Нам нужно ограничиться отрезком $[-π; 2π]$.

Шаг 1: Вычислим, какие значения $t = n$ лежат на отрезке $[-π; 2π]$.

• Из условия задачи: $-π \leq t \leq 2π$, где $π \approx 3.1416$.
• Подставляем значения для $n$:
  • $-π \approx -3.1416$
  • $2π \approx 6.2832$

  Нужно выбрать целые числа $n$, которые лежат между $-π$ и $2π$. Проверим несколько значений:

  • $t = -4$: Это меньше чем $-π$, поэтому это значение исключаем.
  • $t = 7$: Это больше чем $2π$, исключаем.
  • $t = -3$: Это больше чем $-π$, но меньше чем $2π$, поэтому оно подходит.
  • $t = -2$: Оно также лежит на отрезке $[-π; 2π]$, подходит.
  • $t = -1$: Лежит в пределах отрезка.
  • $t = 0$: Лежит в пределах отрезка.
  • $t = 1$: Лежит в пределах отрезка.
  • $t = 2$: Лежит в пределах отрезка.
  • $t = 3$: Лежит в пределах отрезка.
  • $t = 4$: Лежит в пределах отрезка.
  • $t = 5$: Лежит в пределах отрезка.
  • $t = 6$: Лежит в пределах отрезка.

Шаг 2: Составим итоговый список значений $t$, принадлежащих отрезку $[-π; 2π]$.

Ответ: $-3; -2; -1; 0; 1; 2; 3; 4; 5; 6.$

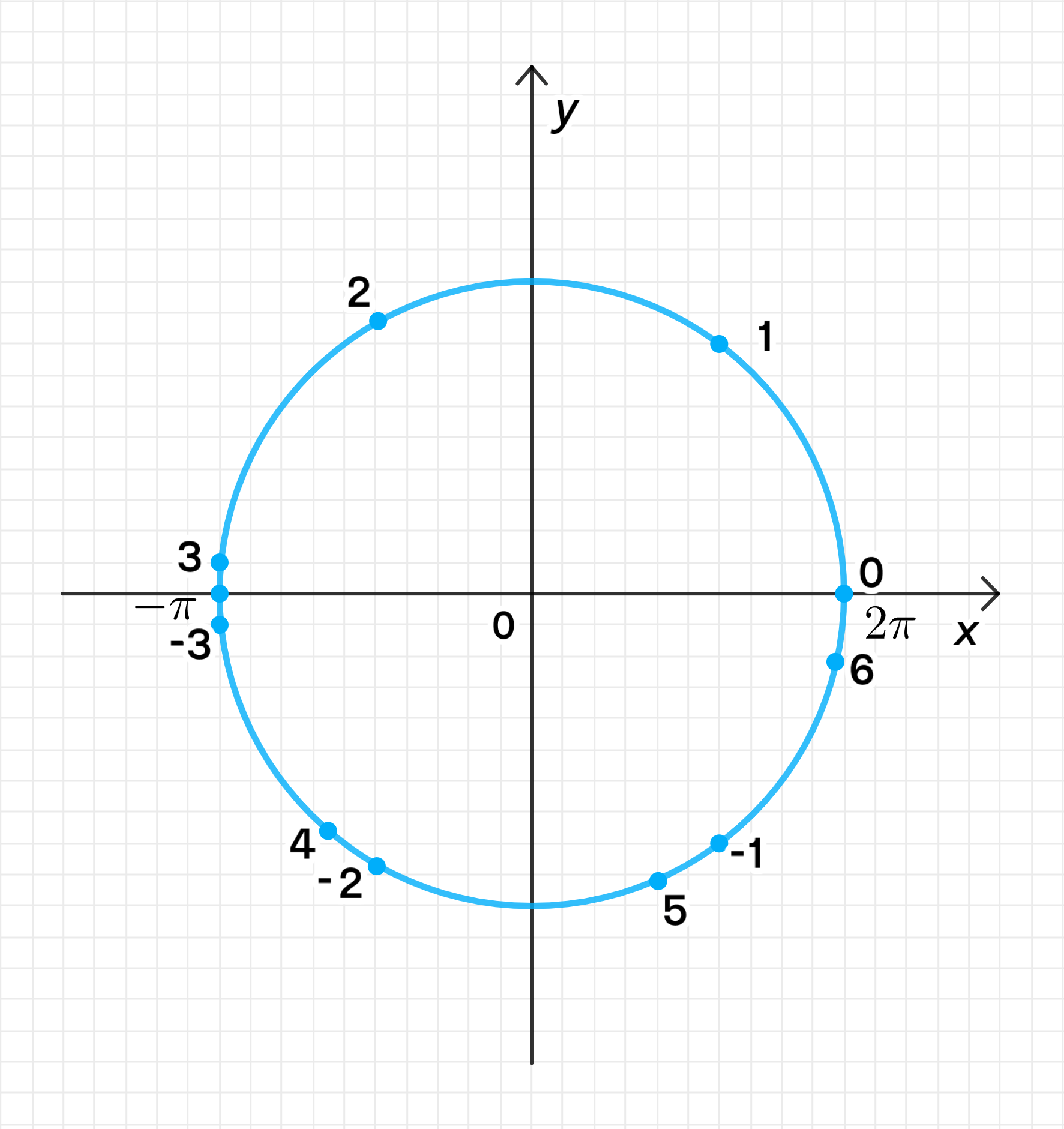
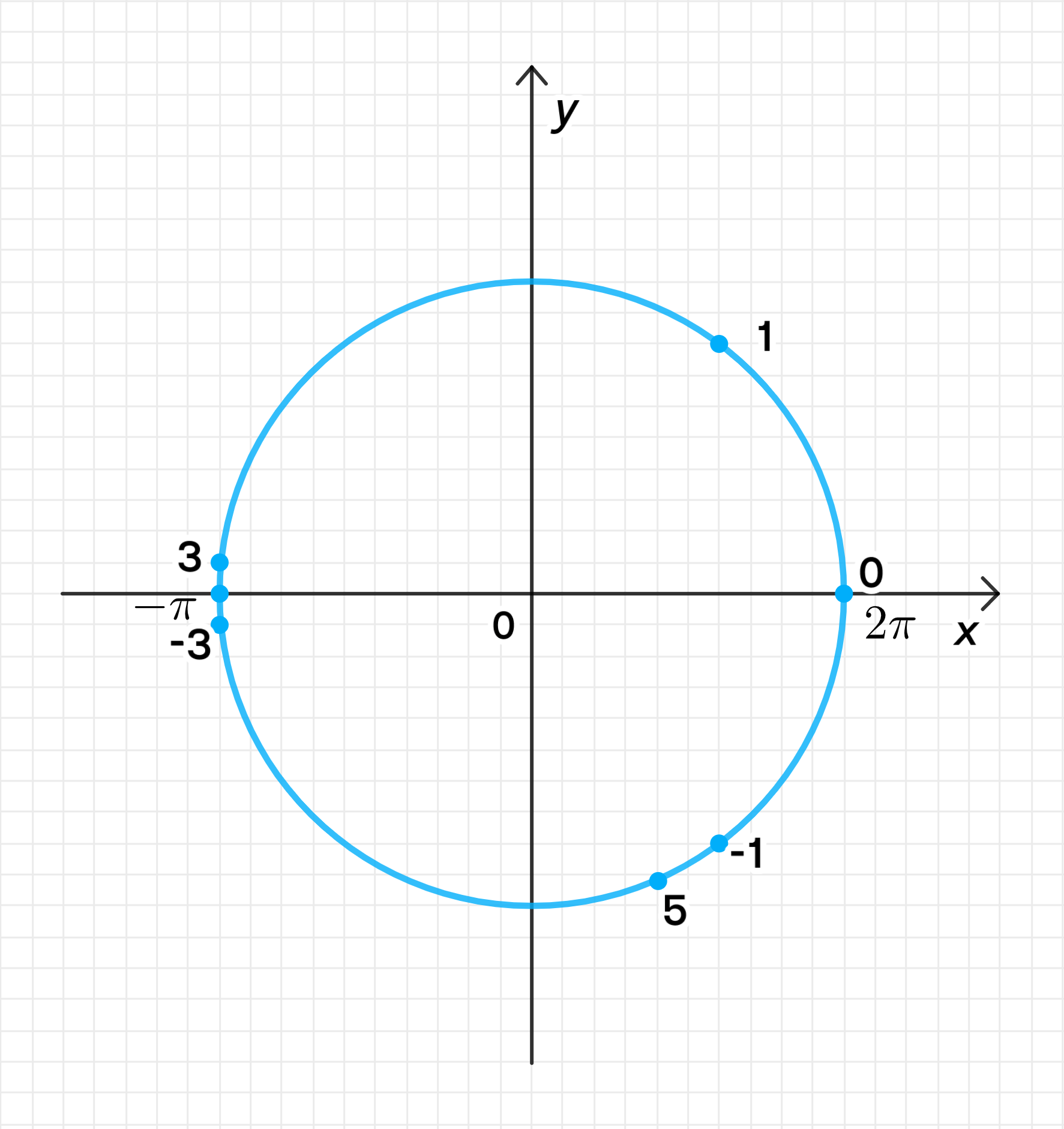
На числовой окружности:

Для каждого целого числа, лежащего на отрезке, можно отметить точку на окружности. На числовой окружности точка $t = n$ будет соответствовать углу, который равен $n$ радианам. Отметим все целые значения на окружности.

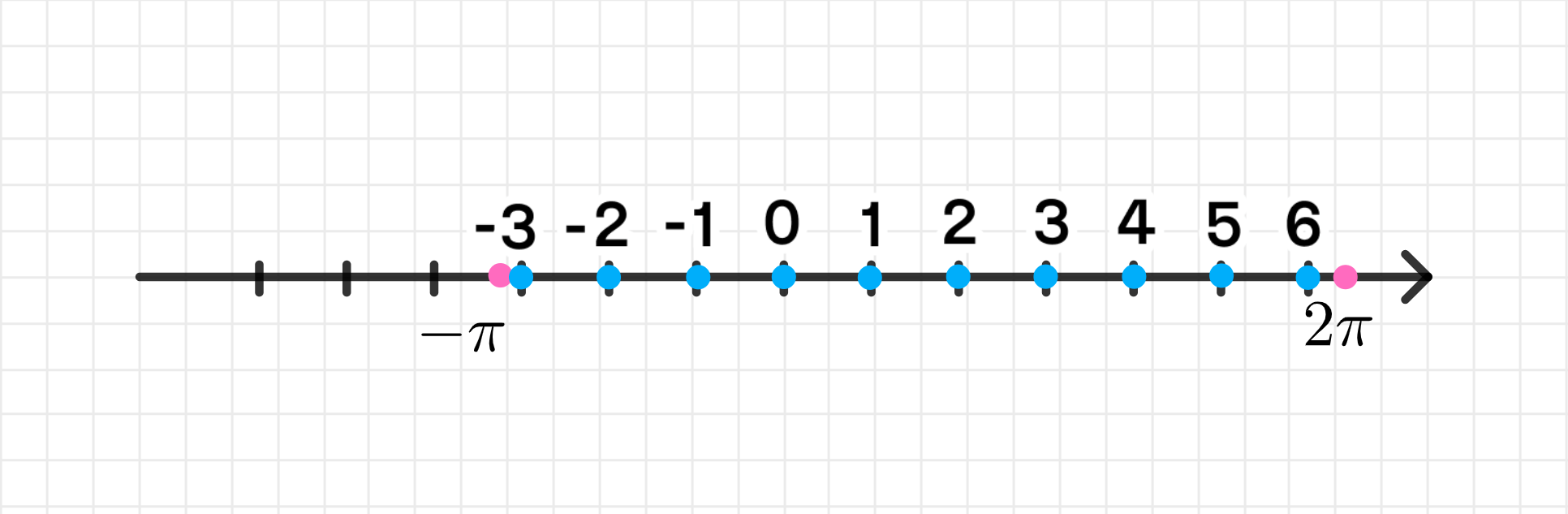
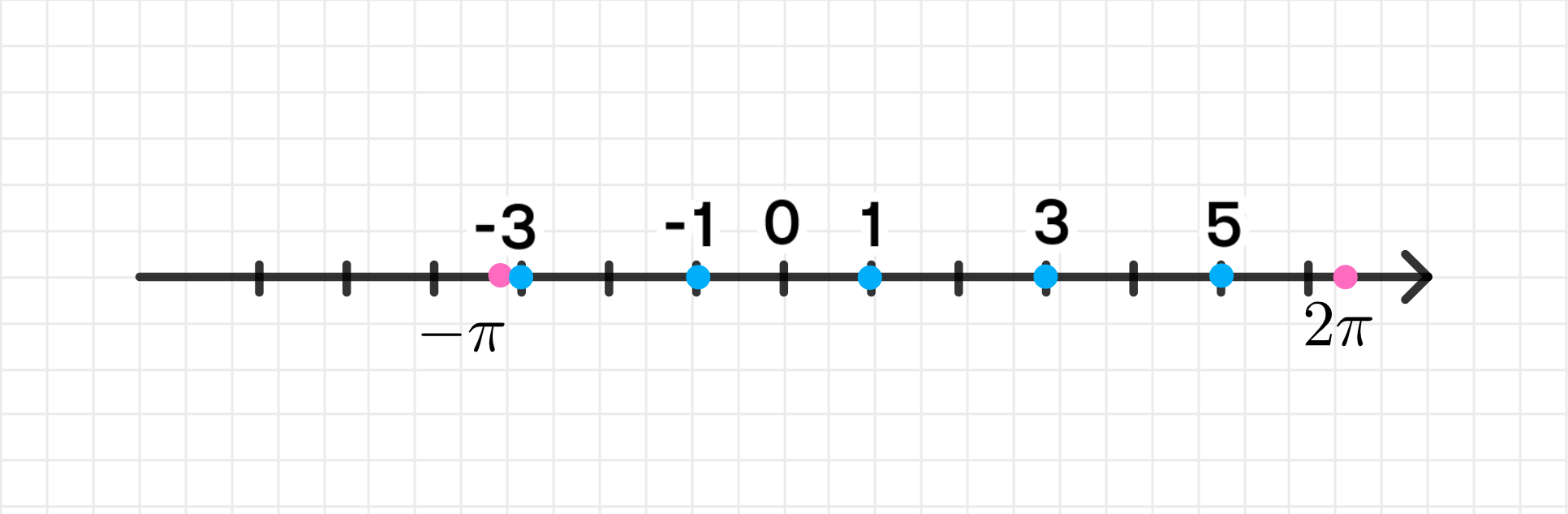
На числовой прямой:

На числовой прямой эти же точки будут расположены как целые числа от $-3$ до $6$. Каждое значение будет просто отмечено на линии.

б) $t = \frac{1}{2} + 2n$

Задание функции $t = \frac{1}{2} + 2n$

Здесь $t$ зависит от переменной $n$, и формула описывает линейную зависимость с шагом 2. Нам нужно определить, какие значения $t$ лежат в интервале от $-π$ до $2π$.

Шаг 1: Найдем границы интервала.

Мы знаем, что:

$$-π \leq t \leq 2π \quad \text{или} \quad -3.1416 \leq t \leq 6.2832$$

Подставляем значения для $n$:

• Для $n = -2$, получаем $t = \frac{1}{2} — 4 = -3.5$, что меньше $-π$, поэтому это значение не подходит.
• Для $n = -1$, получаем $t = \frac{1}{2} — 2 = -1.5$, это значение лежит на отрезке.
• Для $n = 0$, получаем $t = \frac{1}{2} = 0.5$, это значение лежит на отрезке.
• Для $n = 1$, получаем $t = \frac{1}{2} + 2 = 2.5$, это значение лежит на отрезке.
• Для $n = 2$, получаем $t = \frac{1}{2} + 4 = 4.5$, это значение лежит на отрезке.
• Для $n = 3$, получаем $t = \frac{1}{2} + 6 = 6.5$, что больше $2π$, это значение не подходит.

Шаг 2: Составим итоговый список значений $t$.

Ответ: $-1.5; 0.5; 2.5; 4.5.$

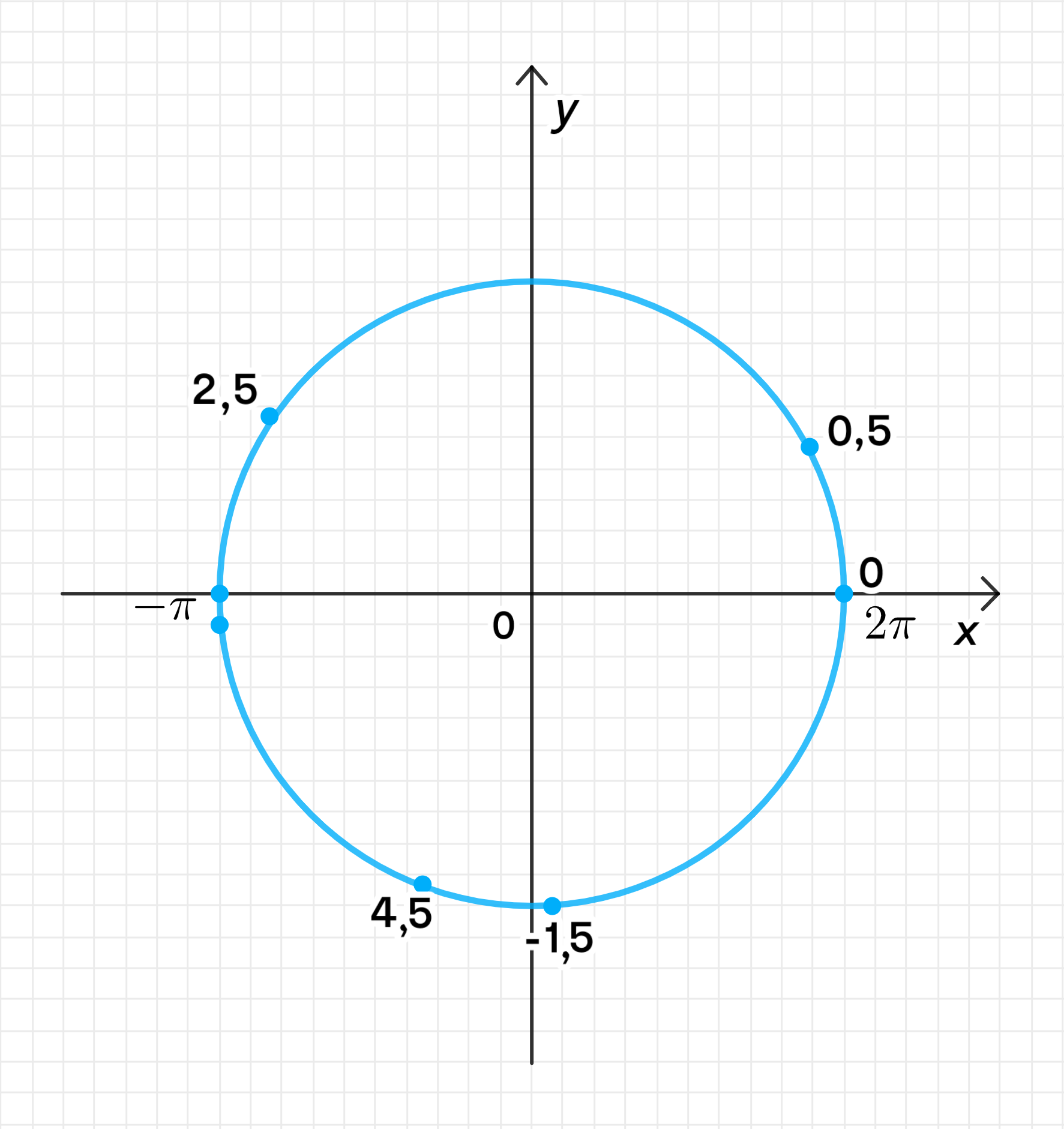
На числовой окружности:

Для каждого из значений $t$, таких как $-1.5$, $0.5$, $2.5$ и $4.5$, можно отметить соответствующие точки на числовой окружности.

На числовой прямой:

Точки $-1.5$, $0.5$, $2.5$ и $4.5$ будут располагаться на прямой. Мы отметим их на линии от $-π$ до $2π$.

в) $t = 2n + 1$

Задание функции $t = 2n + 1$

Здесь $t$ зависит от переменной $n$, и это выражение дает нечетные числа. Мы ищем такие $n$, при которых $t$ будет лежать на отрезке $[-π; 2π]$.

Шаг 1: Найдем границы интервала.

Подставляем значения для $n$:

• Для $n = -3$, получаем $t = 2(-3) + 1 = -5$, это значение меньше $-π$, исключаем.
• Для $n = -2$, получаем $t = 2(-2) + 1 = -3$, это значение лежит на отрезке.
• Для $n = -1$, получаем $t = 2(-1) + 1 = -1$, это значение лежит на отрезке.
• Для $n = 0$, получаем $t = 2(0) + 1 = 1$, это значение лежит на отрезке.
• Для $n = 1$, получаем $t = 2(1) + 1 = 3$, это значение лежит на отрезке.
• Для $n = 2$, получаем $t = 2(2) + 1 = 5$, это значение лежит на отрезке.
• Для $n = 3$, получаем $t = 2(3) + 1 = 7$, это значение больше $2π$, исключаем.

Шаг 2: Составим итоговый список значений $t$.

Ответ: $-3; -1; 1; 3; 5.$

На числовой окружности:

Для каждого из значений $t$, таких как $-3$, $-1$, $1$, $3$ и $5$, можно отметить соответствующие точки на числовой окружности.

На числовой прямой:

Точки $-3$, $-1$, $1$, $3$ и $5$ будут располагаться на прямой. Мы отметим их на линии от $-π$ до $2π$.

г) $t = \frac{1}{3} + \frac{3n}{2}$

Задание функции $t = \frac{1}{3} + \frac{3n}{2}$

Здесь $t$ зависит от переменной $n$, и функция имеет более сложную форму. Нам нужно найти такие значения $n$, при которых $t$ лежит на отрезке $[-π; 2π]$.

Шаг 1: Найдем границы интервала.

Подставляем значения для $n$:

• Для $n = -3$, получаем $t = \frac{1}{3} — \frac{9}{2} = -\frac{25}{6} = -4.167$, это значение меньше $-π$, исключаем.
• Для $n = -2$, получаем $t = \frac{1}{3} — \frac{6}{2} = -2.6667$, это значение лежит на отрезке.
• Для $n = -1$, получаем $t = \frac{1}{3} — \frac{3}{2} = -1.1667$, это значение лежит на отрезке.
• Для $n = 0$, получаем $t = \frac{1}{3} = 0.3333$, это значение лежит на отрезке.
• Для $n = 1$, получаем $t = \frac{1}{3} + \frac{3}{2} = 1.8333$, это значение лежит на отрезке.
• Для $n = 2$, получаем $t = \frac{1}{3} + 3 = 3.3333$, это значение лежит на отрезке.
• Для $n = 3$, получаем $t = \frac{1}{3} + \frac{9}{2} = 4.8333$, это значение лежит на отрезке.
• Для $n = 4$, получаем $t = \frac{1}{3} + 6 = 6.3333$, это значение больше $2π$, исключаем.

Шаг 2: Составим итоговый список значений $t$.

Ответ: $-2\frac{2}{3}; -1\frac{1}{6}; \frac{1}{3}; 1\frac{5}{6}; 3\frac{1}{3}; 4\frac{5}{6}.$

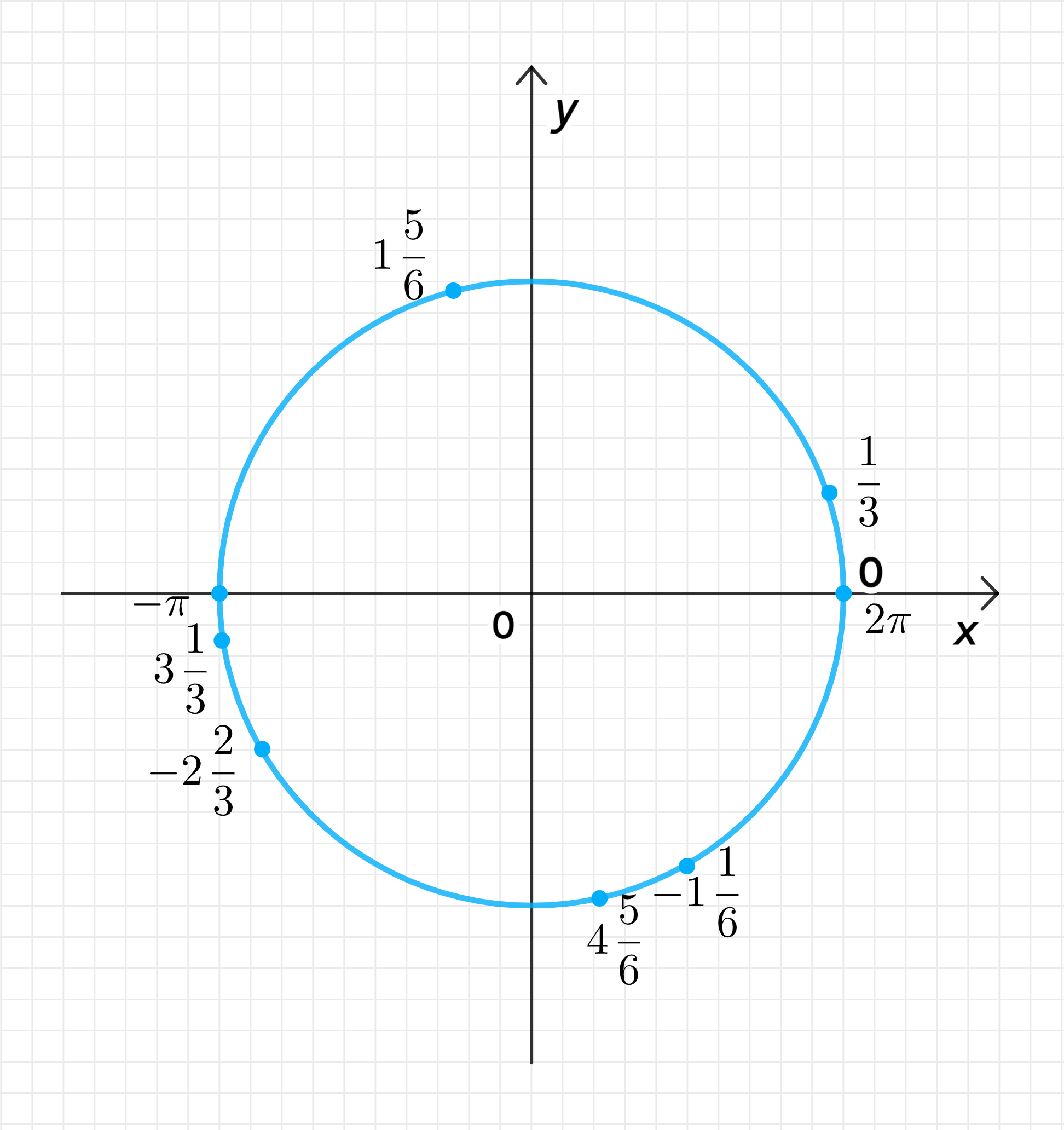
На числовой окружности:

Для каждого из значений $t$, таких как $-2\frac{2}{3}$, $-1\frac{1}{6}$, $\frac{1}{3}$, $1\frac{5}{6}$, $3\frac{1}{3}$, $4\frac{5}{6}$, можно отметить соответствующие точки на числовой окружности.

На числовой прямой:

Точки $-2\frac{2}{3}$, $-1\frac{1}{6}$, $\frac{1}{3}$, $1\frac{5}{6}$, $3\frac{1}{3}$, $4\frac{5}{6}$ будут располагаться на прямой. Мы отметим их на линии от $-π$ до $2π$.

Итоговые ответы:

а) $-3; -2; -1; 0; 1; 2; 3; 4; 5; 6$

б) $-1,5; 0,5; 2,5; 4,5$

в) $-3; -1; 1; 3; 5$

г) $-2\frac{2}{3}; -1\frac{1}{6}; \frac{1}{3}; 1\frac{5}{6}; 3\frac{1}{3}; 4\frac{5}{6}$