Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 11.6 Профильный Уровень Мордкович — Подробные Ответы
Найдите на числовой окружности точку, которая соответствует заданному числу:
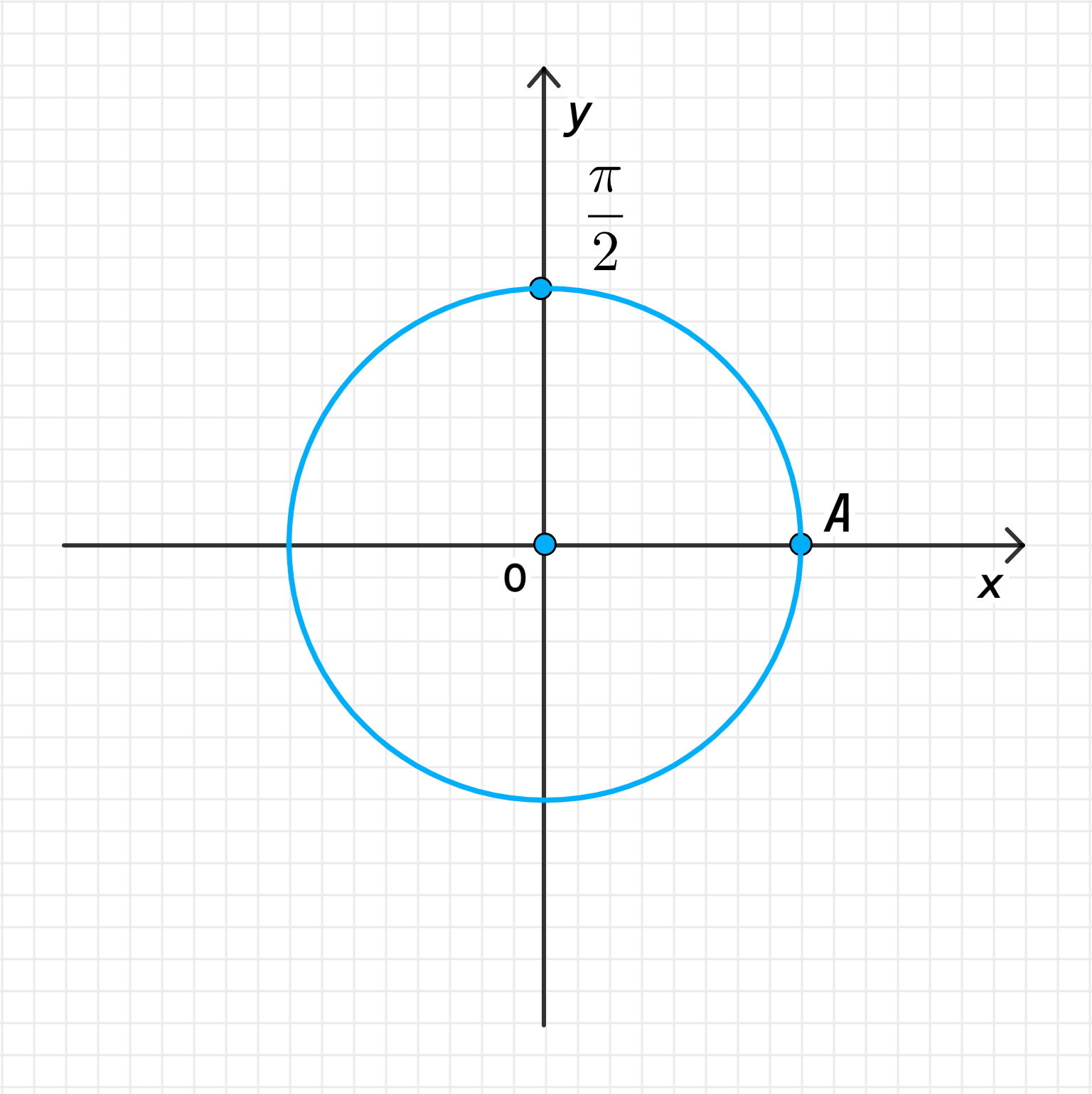
а)
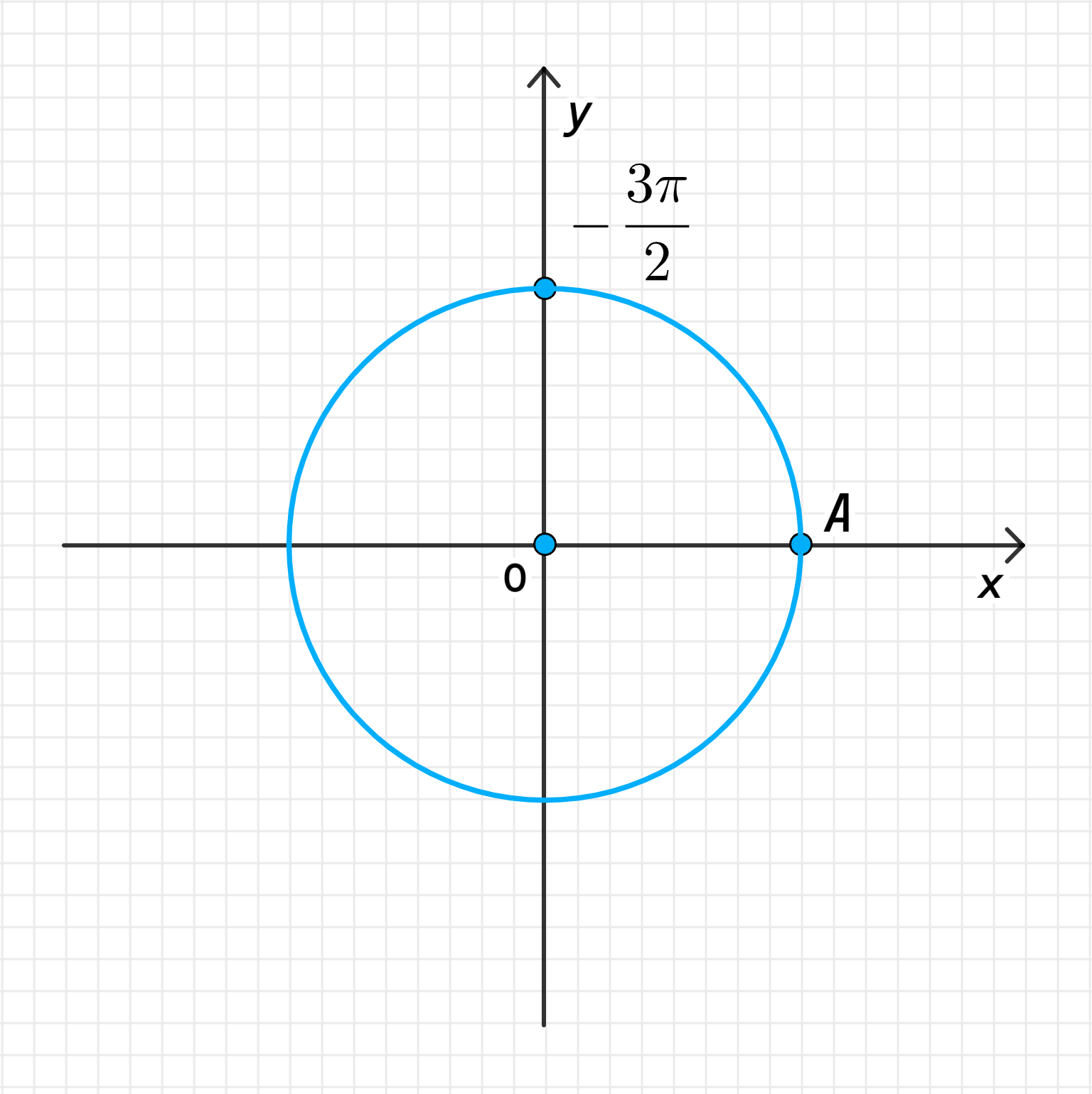
б)
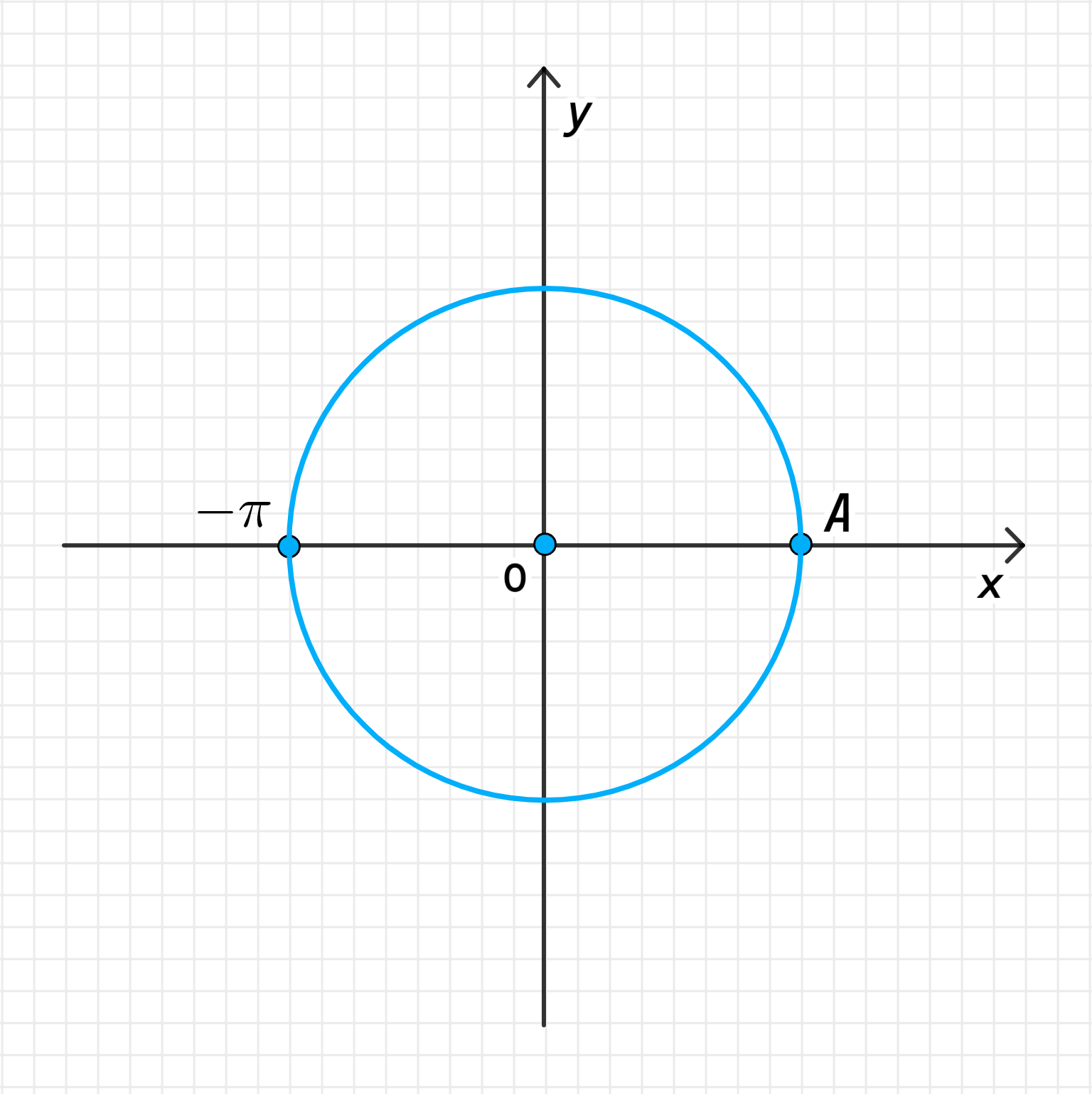
в)
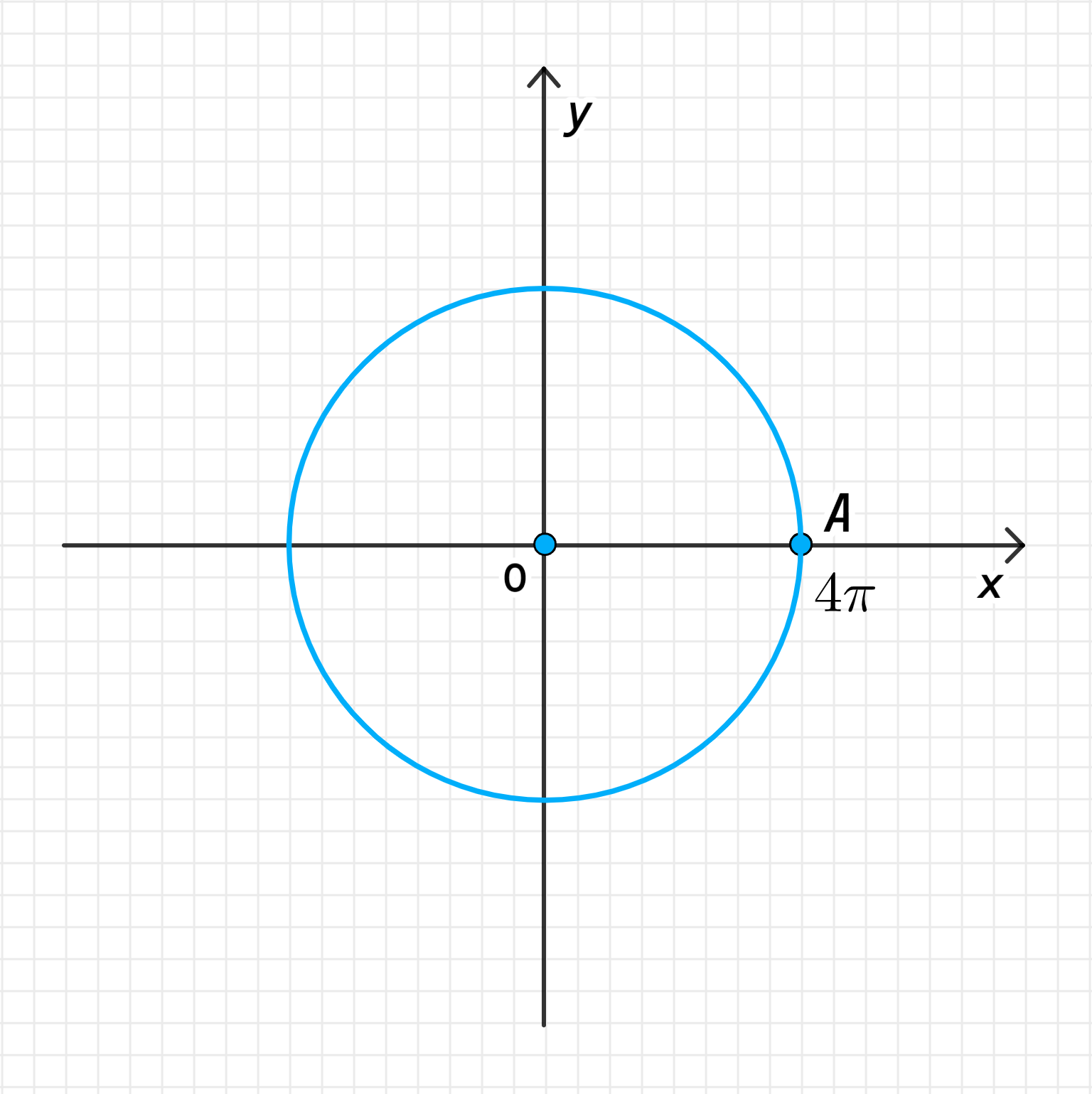
г)
а) Точка ;
Соответствует повороту точки на угол против часовой стрелки;
То есть искомой точкой является точка :
б) Точка ;
;
Соответствует повороту точки на угол против часовой стрелки;
То есть искомой точкой является точка :
в) Точка ;
;
Соответствует повороту точки на угол против часовой стрелки;
То есть искомой точкой является точка :
г) Точка ;
;
Соответствует повороту точки на угол против часовой стрелки;
То есть искомой точкой является точка :
а) Точка ;
- Для точки мы имеем угол поворота, равный , то есть . Это означает, что точка поворачивается на угол против часовой стрелки от своей начальной позиции.
- Чтобы понять, где окажется точка после этого поворота, мы можем представить себе, что точка находится на окружности радиусом . После поворота на угол против часовой стрелки точка переместится в новое положение, которое будет на (или радиан) от начальной точки.
- Соответственно, искомой точкой будет точка , которая расположена на окружности на расстоянии радиан от точки . Это означает, что точка лежит в четверти окружности, которая начинается с точки и продолжается против часовой стрелки.
б) Точка ;
- Для точки мы сначала представляем, что угол поворота равен радиан. Это означает, что точка будет поворачиваться на угол против часовой стрелки. При этом знак минус указывает, что мы поворачиваемся по часовой стрелке на радиан, то есть на половину окружности.
- Сначала вычислим эквивалентный угол для положительного значения. Мы знаем, что полный угол окружности равен , и, если мы поворачиваемся на , то это эквивалентно повороту на угол:
Это подтверждает, что мы сделали поворот на угол радиан (или 180°) против часовой стрелки.
- В результате поворота на угол против часовой стрелки точка перемещается на противоположную сторону окружности и достигает точки .
в) Точка ;
- В данном случае точка перемещается на угол радиан. Чтобы понять, как это выглядит, нужно рассмотреть, что такое угол . Поворот на радиан (или 360°) возвращает нас в исходное положение. Следовательно, поворот на угол эквивалентен повороту на угол:
Это означает, что точка возвращается в свое начальное положение после двух полных оборотов вокруг окружности.
- Поворот на угол радиан (или два полных оборота) не изменяет положение точки , так как точка возвращается в исходную точку.
- Следовательно, после поворота на радиан искомой точкой будет снова точка .
г) Точка ;
- Теперь рассмотрим точку . Это означает, что мы поворачиваем точку по часовой стрелке на угол радиан, что эквивалентно повороту на угол .
- Чтобы привести угол в эквивалентную положительную форму, нам нужно прибавить (полный оборот), так как поворот по часовой стрелке на — это эквивалентный поворот против часовой стрелки на угол :
Таким образом, мы можем рассматривать этот поворот как поворот на против часовой стрелки.
- Поворот на угол против часовой стрелки возвращает точку в положение, которое мы уже рассматривали в пункте (а). Таким образом, искомой точкой снова будет точка .