ГДЗ по Алгебре 10 Класс Номер 11.7 Профильный Уровень Мордкович — Подробные Ответы

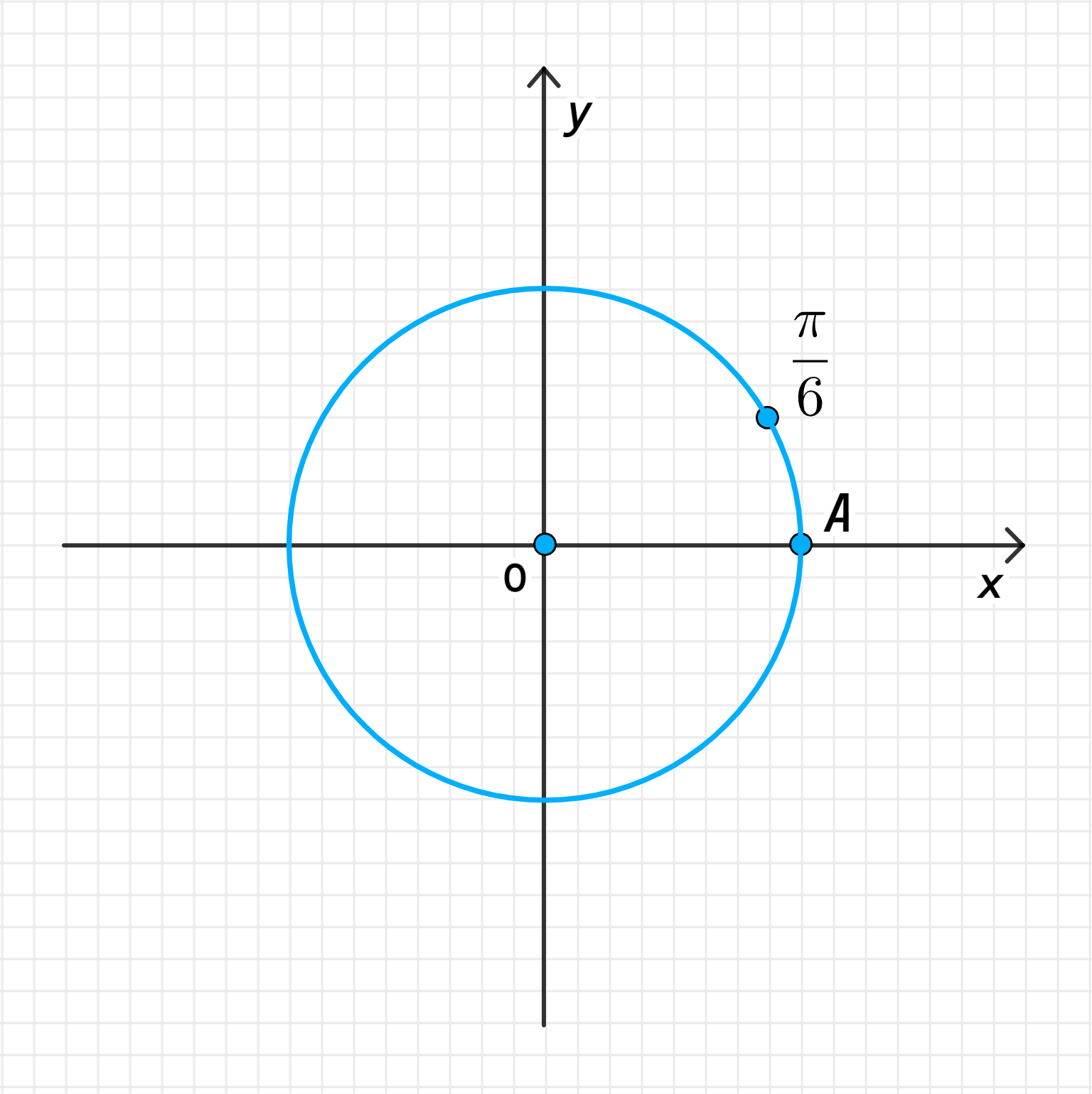
а) $\frac{\pi}{6}$

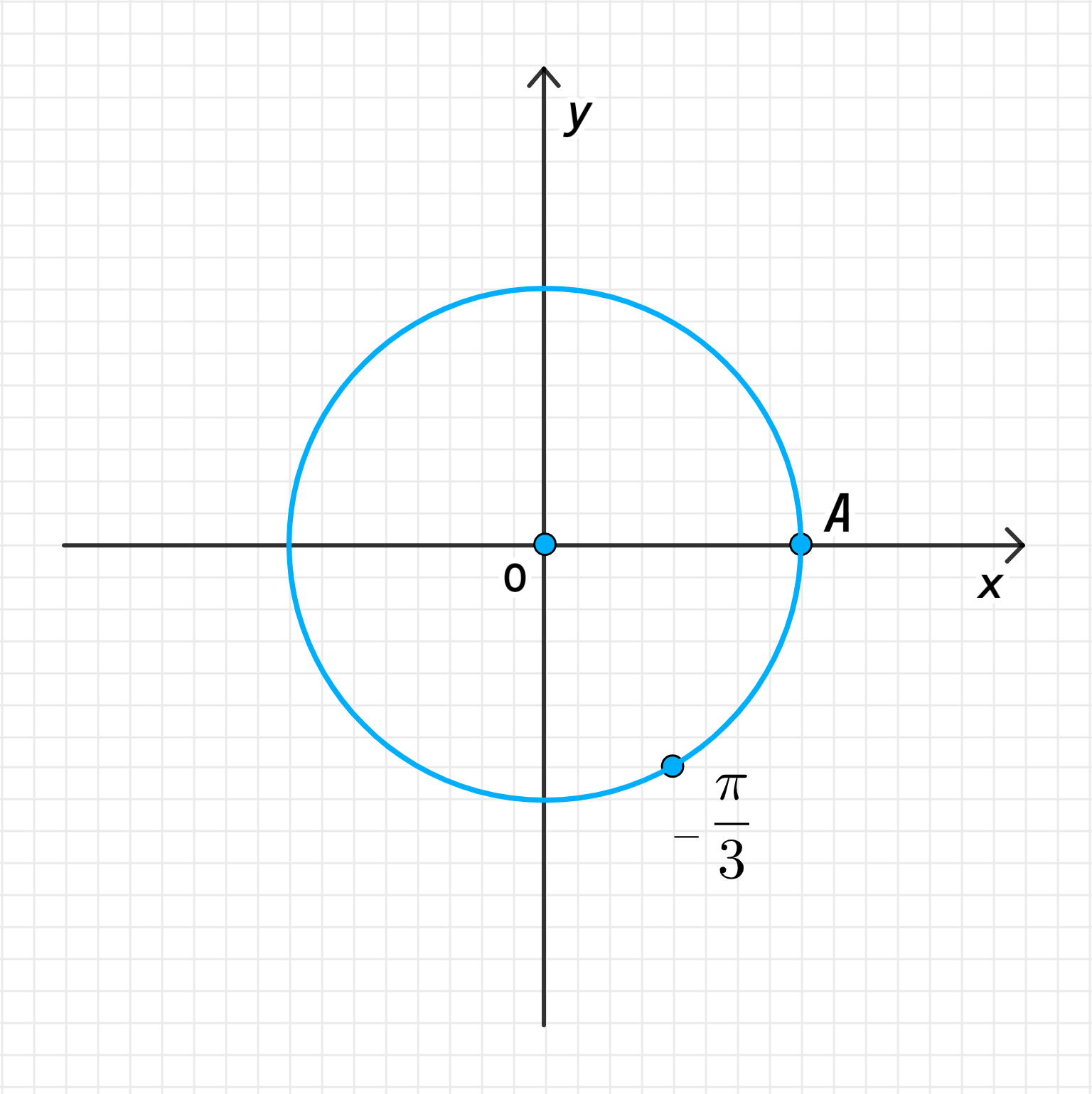
б) $-\frac{\pi }{3}$

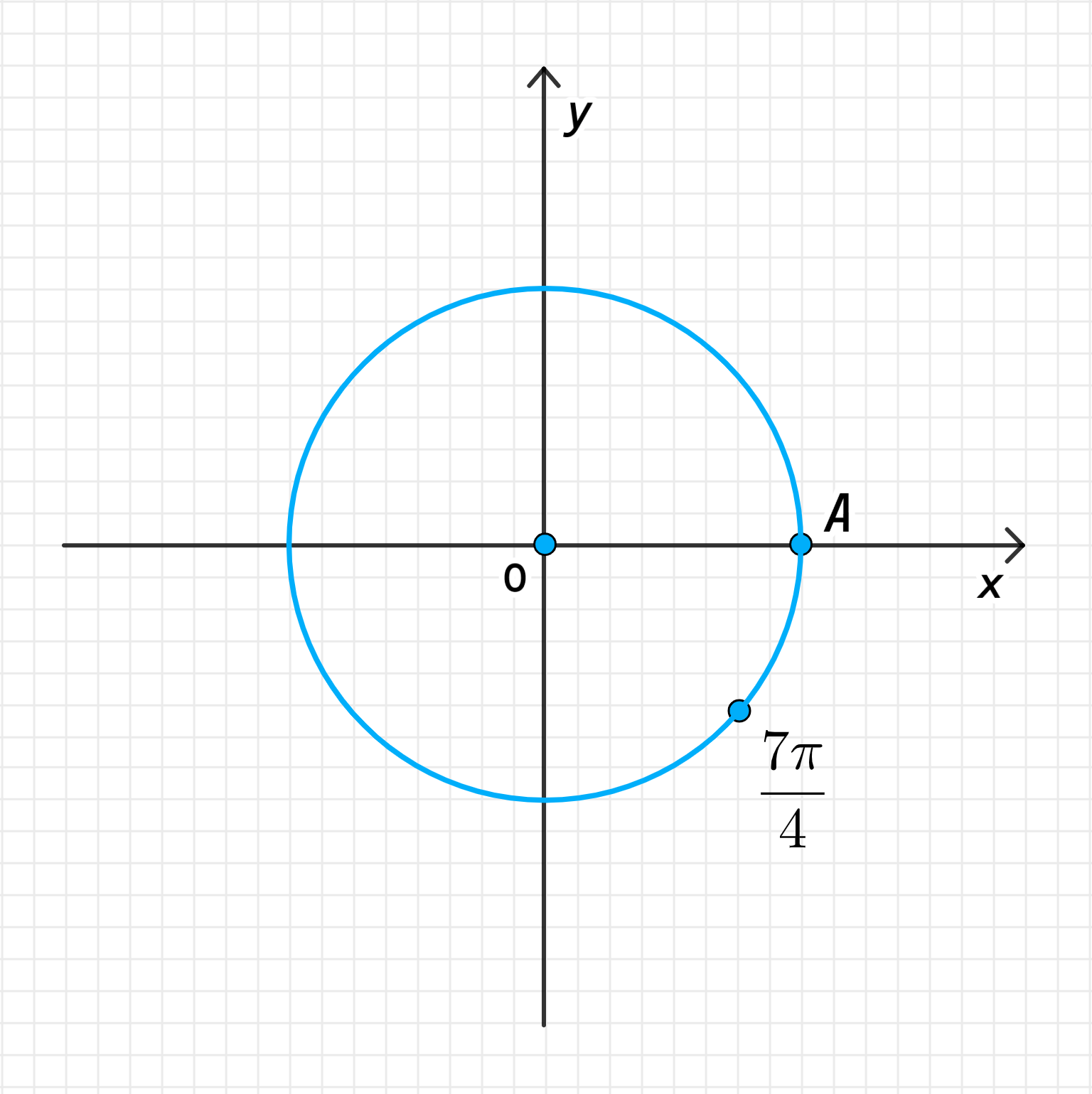
в) $\frac{7\pi}{4}$

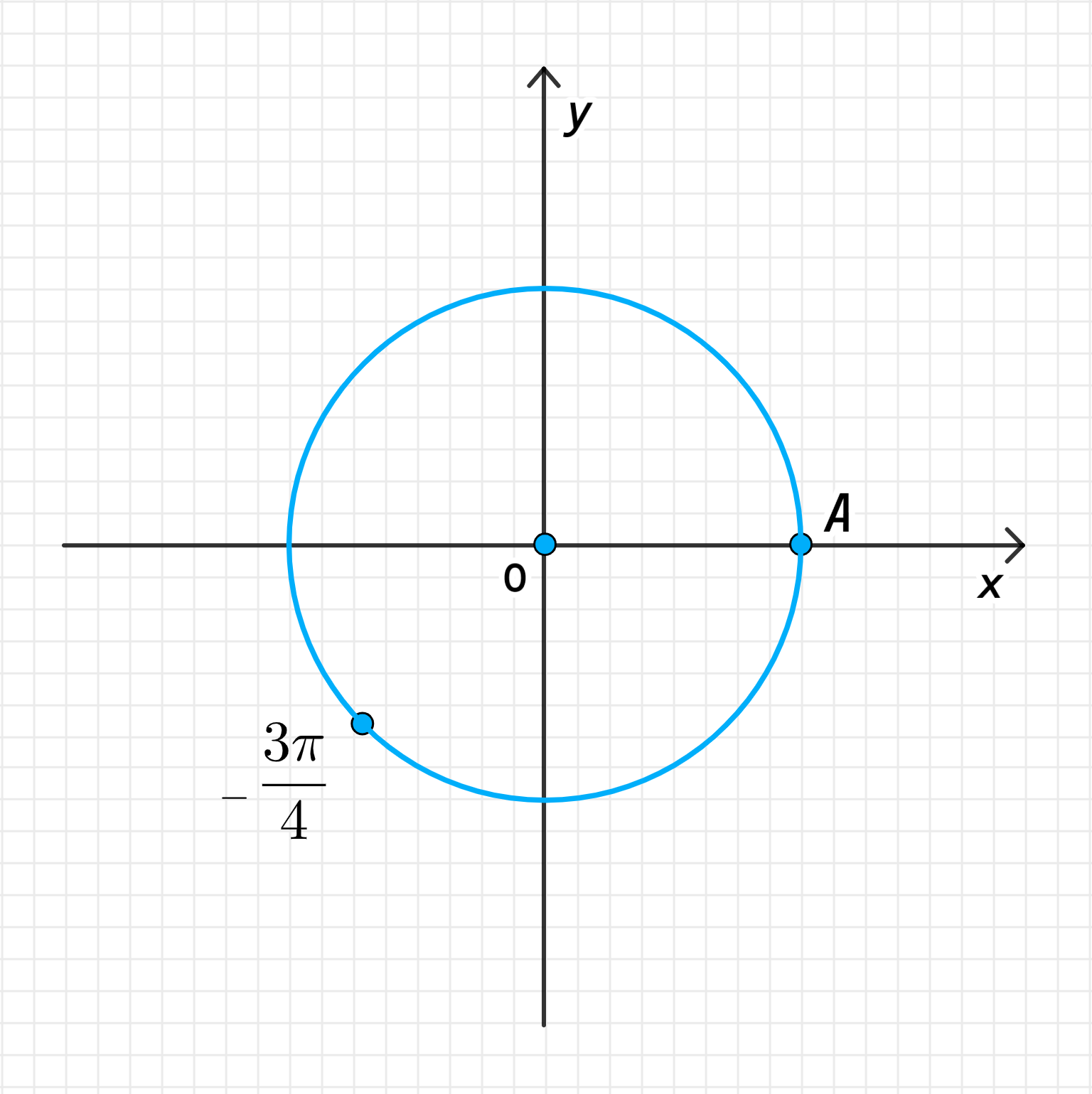
г) $-\frac{3\pi }{4}$

а) Число $\frac{\pi}{6}$:

Соответствует повороту точки $A$ на угол $\frac{\pi}{6}$ против часовой стрелки;

То есть искомая точка $M$ делит дугу $AB$ в отношении:

$$\frac{AM}{AB} = \frac{\pi}{6} : \frac{\pi}{2} = \frac{\pi}{6} \cdot \frac{2}{\pi} = \frac{2}{6} = \frac{1}{3};$$

На числовой окружности:

б) Число $\left(-\frac{\pi}{3}\right)$:

$a = 2\pi — \frac{\pi}{3} = \frac{5\pi}{3} = \frac{9\pi}{6} + \frac{\pi}{6} = \frac{3\pi}{2} + \frac{\pi}{6}$;

Соответствует повороту точки $D$ на угол $\frac{\pi}{6}$ против часовой стрелки;

То есть искомая точка $M$ делит дугу $DA$ в отношении:

$$\frac{DM}{DA} = \frac{\pi}{6} : \frac{\pi}{2} = \frac{\pi}{6} \cdot \frac{2}{\pi} = \frac{2}{6} = \frac{1}{3};$$

На числовой окружности:

в) Число $\frac{7\pi}{4}$:

$a = \frac{7\pi}{4} = \frac{6\pi}{4} + \frac{\pi}{4} = \frac{3\pi}{2} + \frac{\pi}{4}$;

Соответствует повороту точки $D$ на угол $\frac{\pi}{4}$ против часовой стрелки;

То есть искомая точка $M$ делит дугу $DA$ в отношении:

$$\frac{DM}{DA} = \frac{\pi}{4} : \frac{\pi}{2} = \frac{\pi}{4} \cdot \frac{2}{\pi} = \frac{2}{4} = \frac{1}{2};$$

На числовой окружности:

г) Число $\left(-\frac{3\pi}{4}\right)$:

$a = 2\pi — \frac{3\pi}{4} = \frac{5\pi}{4} = \pi + \frac{\pi}{4}$;

Соответствует повороту точки $C$ на угол $\frac{\pi}{4}$ против часовой стрелки;

То есть искомая точка $M$ делит дугу $CD$ в отношении:

$$\frac{CM}{CD} = \frac{\pi}{4} : \frac{\pi}{2} = \frac{\pi}{4} \cdot \frac{2}{\pi} = \frac{2}{4} = \frac{1}{2};$$

На числовой окружности:

а) Число $\frac{\pi}{6}$:

1. Поворот точки $A$ на угол $\frac{\pi}{6}$:

   Для числа $\frac{\pi}{6}$ мы рассматриваем поворот точки $A$ на угол $\frac{\pi}{6}$ против часовой стрелки. Это означает, что точка $A$ будет перемещаться по окружности на угол, равный $\frac{\pi}{6}$ радиан (или 30 градусов) против часовой стрелки.

   Поскольку полный оборот вокруг окружности составляет $2\pi$ радиан, то угол $\frac{\pi}{6}$ — это небольшая часть окружности, приблизительно равная 1/12 полного оборота. Таким образом, точка $A$ смещается от своей исходной позиции на угол $\frac{\pi}{6}$ против часовой стрелки, и новая точка на окружности будет находиться на этом расстоянии от точки $A$.

2. Деление дуги $AB$ в отношении:

   На окружности дуга, соответствующая углу $\frac{\pi}{6}$, делит дугу $AB$ между точками $A$ и $B$, которая составляет $\frac{\pi}{2}$ радиан. Мы можем выразить это отношение через дробь, где числитель — это угол $\frac{\pi}{6}$, а знаменатель — угол $\frac{\pi}{2}$, соответствующий дуге $AB$:

   $$\frac{AM}{AB} = \frac{\frac{\pi}{6}}{\frac{\pi}{2}} = \frac{\pi}{6} \cdot \frac{2}{\pi} = \frac{2}{6} = \frac{1}{3}.$$

   Таким образом, точка $M$ делит дугу $AB$ в отношении 1:3, что означает, что точка $M$ находится на третьем пути от точки $A$ до точки $B$ по окружности.

3. Графическое изображение:

   На числовой окружности, где каждый угол представлен точкой на окружности, точка $M$ будет находиться примерно на 1/3 пути от точки $A$ до точки (B.

б) Число $\left(-\frac{\pi}{3}\right)$:

1. Эквивалентный угол для $-\frac{\pi}{3}$:

   Мы имеем отрицательное значение угла $-\frac{\pi}{3}$, что означает поворот по часовой стрелке. Чтобы найти эквивалентный угол в положительном направлении, нам нужно добавить полный оборот $2\pi$, так как повороты на полный круг эквивалентны:

   $$a = 2\pi — \frac{\pi}{3} = \frac{5\pi}{3} = \frac{9\pi}{6} + \frac{\pi}{6} = \frac{3\pi}{2} + \frac{\pi}{6}.$$

   Это означает, что поворот на угол $-\frac{\pi}{3}$ эквивалентен повороту на угол $\frac{\pi}{6}$ против часовой стрелки.

2. Поворот точки $D$ на угол $\frac{\pi}{6}$:

   Точка $D$ будет поворачиваться на угол $\frac{\pi}{6}$ против часовой стрелки. После этого поворота точка $D$ переместится на окружности на угол $\frac{\pi}{6}$ в направлении против часовой стрелки, и она попадет на новую позицию, соответствующую точке $M$.

3. Деление дуги $DA$ в отношении:

   Теперь, рассмотрим, как точка $M$ делит дугу $DA$. Дуга $DA$ имеет длину $\frac{\pi}{2}$ радиан (так как она равна половине полного угла окружности). Точка $M$ делит эту дугу в том же отношении, что и в предыдущем случае:

   $$\frac{DM}{DA} = \frac{\frac{\pi}{6}}{\frac{\pi}{2}} = \frac{\pi}{6} \cdot \frac{2}{\pi} = \frac{2}{6} = \frac{1}{3}.$$

   Это означает, что точка $M$ находится на пути от точки $D$ до точки $A$, занимая 1/3 этого пути.

4. Графическое изображение:

   На числовой окружности точка $M$ будет расположена на 1/3 пути от точки $D$ до точки $A$.

в) Число $\frac{7\pi}{4}$:

1. Эквивалентный угол для $\frac{7\pi}{4}$:

   Угол $\frac{7\pi}{4}$ — это более чем один полный оборот, так как $2\pi$ составляет полный круг. Для того чтобы найти эквивалентный угол, который меньше или равен $2\pi$, мы разбиваем $\frac{7\pi}{4}$ на более простые части:

   $$a = \frac{7\pi}{4} = \frac{6\pi}{4} + \frac{\pi}{4} = \frac{3\pi}{2} + \frac{\pi}{4}.$$

   Это означает, что поворот на угол $\frac{7\pi}{4}$ — это эквивалентно повороту на угол $\frac{\pi}{4}$ после одного полного оборота (то есть после поворота на $2\pi$).

2. Поворот точки $D$ на угол $\frac{\pi}{4}$:

   Поворот точки $D$ на угол $\frac{\pi}{4}$ против часовой стрелки переместит точку $D$ на новую позицию, которая будет на 45 градусов (или $\frac{\pi}{4}$ радиан) от исходной позиции.

3. Деление дуги $DA$ в отношении:

   Дуга $DA$ снова имеет длину $\frac{\pi}{2}$ радиан. Точка $M$ делит дугу $DA$ в следующем отношении:

   $$\frac{DM}{DA} = \frac{\frac{\pi}{4}}{\frac{\pi}{2}} = \frac{\pi}{4} \cdot \frac{2}{\pi} = \frac{2}{4} = \frac{1}{2}.$$

   Это означает, что точка $M$ делит дугу $DA$ пополам, и будет располагаться ровно на середине этой дуги.

4. Графическое изображение:

   На числовой окружности точка $M$ будет находиться в середине дуги $DA$, что соответствует половине пути от точки $D$ до точки $A$.

г) Число $\left(-\frac{3\pi}{4}\right)$:

1. Эквивалентный угол для $-\frac{3\pi}{4}$:

   Мы имеем угол $-\frac{3\pi}{4}$, что означает поворот по часовой стрелке. Чтобы перевести его в положительный угол, мы прибавим полный оборот $2\pi$:

   $$a = 2\pi — \frac{3\pi}{4} = \frac{5\pi}{4} = \pi + \frac{\pi}{4}.$$

   Это эквивалентно повороту на угол $\frac{\pi}{4}$ против часовой стрелки, начиная с точки $C$.

2. Поворот точки $C$ на угол $\frac{\pi}{4}$:

   Поворот точки $C$ на угол $\frac{\pi}{4}$ против часовой стрелки переместит точку $C$ на новую позицию, которая будет на 45 градусов (или $\frac{\pi}{4}$ радиан) от точки $C$.

3. Деление дуги $CD$ в отношении:

   Дуга $CD$ также имеет длину $\frac{\pi}{2}$ радиан. Точка $M$ делит эту дугу в следующем отношении:

   $$\frac{CM}{CD} = \frac{\frac{\pi}{4}}{\frac{\pi}{2}} = \frac{\pi}{4} \cdot \frac{2}{\pi} = \frac{2}{4} = \frac{1}{2}.$$

   Это означает, что точка $M$ делит дугу $CD$ пополам, и будет располагаться в середине этой дуги.

4. Графическое изображение:

   На числовой окружности точка $M$ будет находиться в середине дуги $CD$, что соответствует половине пути от точки $C$ до точки $D$.