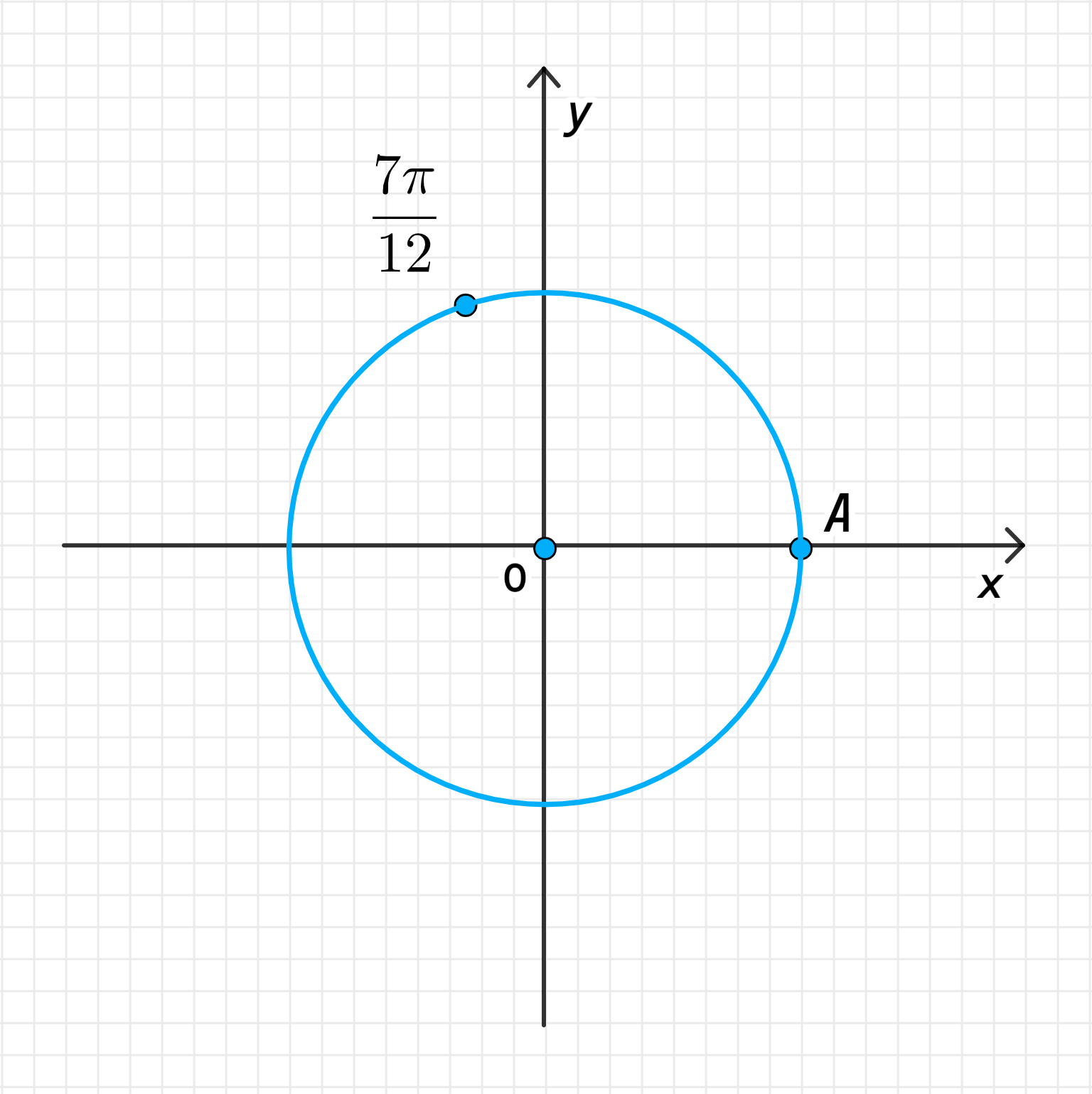Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 11.9 Профильный Уровень Мордкович — Подробные Ответы
а)
б)
в)
г)
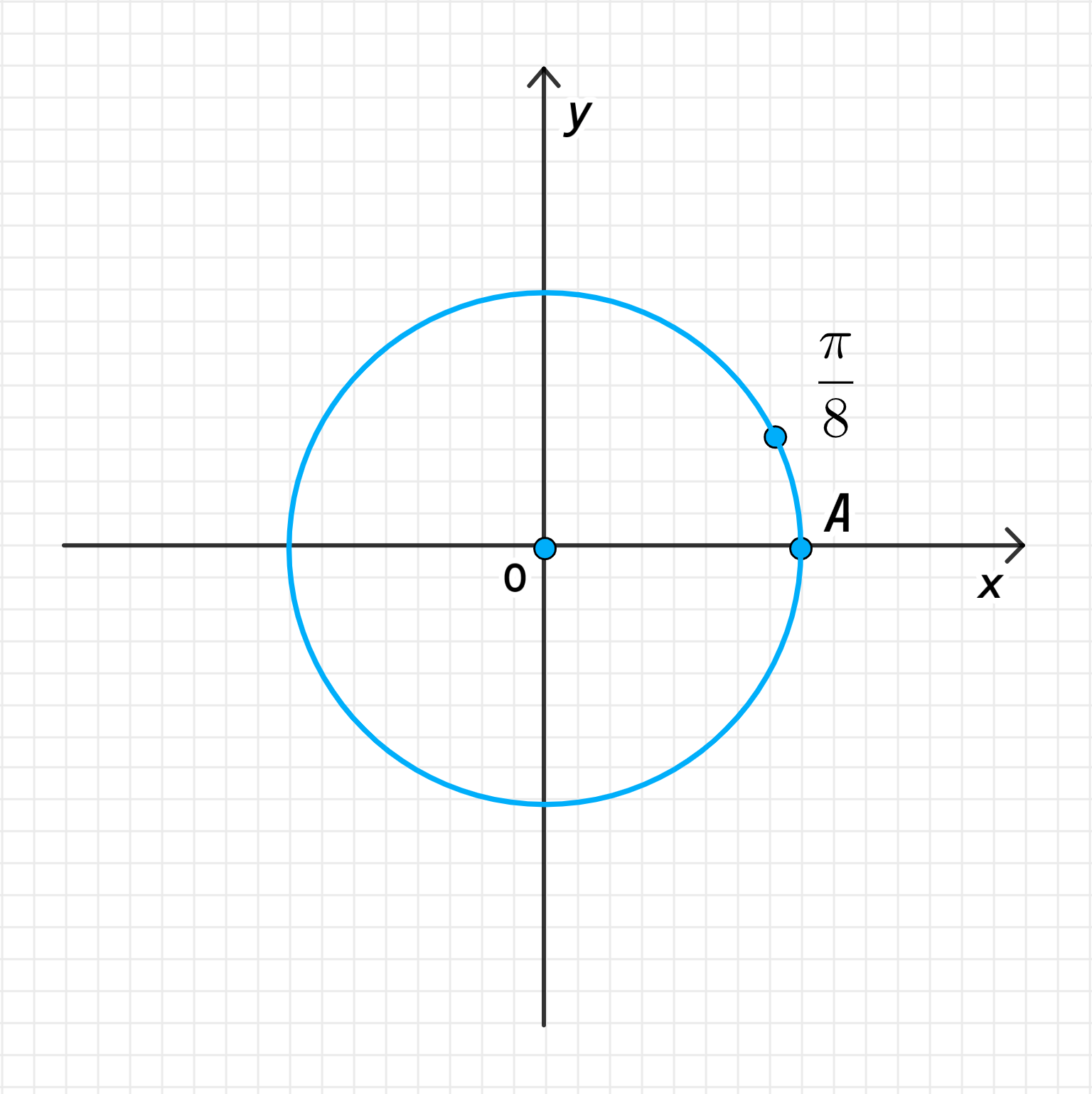
а) Число :
Соответствует повороту точки на угол против часовой стрелки;
То есть искомая точка делит дугу в отношении:
На числовой окружности:
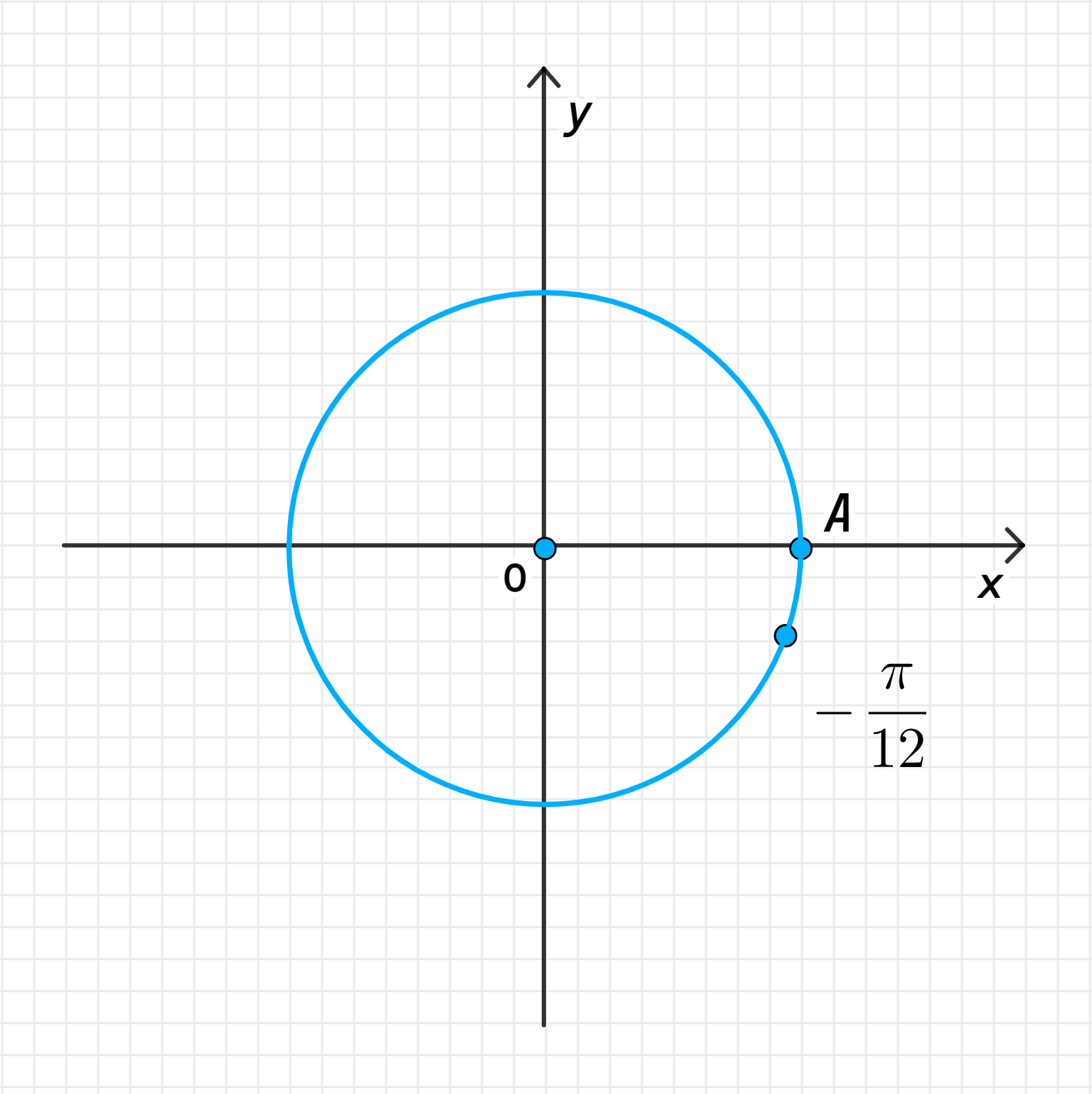
б) Число :
;
Соответствует повороту точки на угол против часовой стрелки;
То есть искомая точка делит дугу в отношении:
На числовой окружности:
в) Число :
;
Соответствует повороту точки на угол против часовой стрелки;
То есть искомая точка делит дугу в отношении:
На числовой окружности:
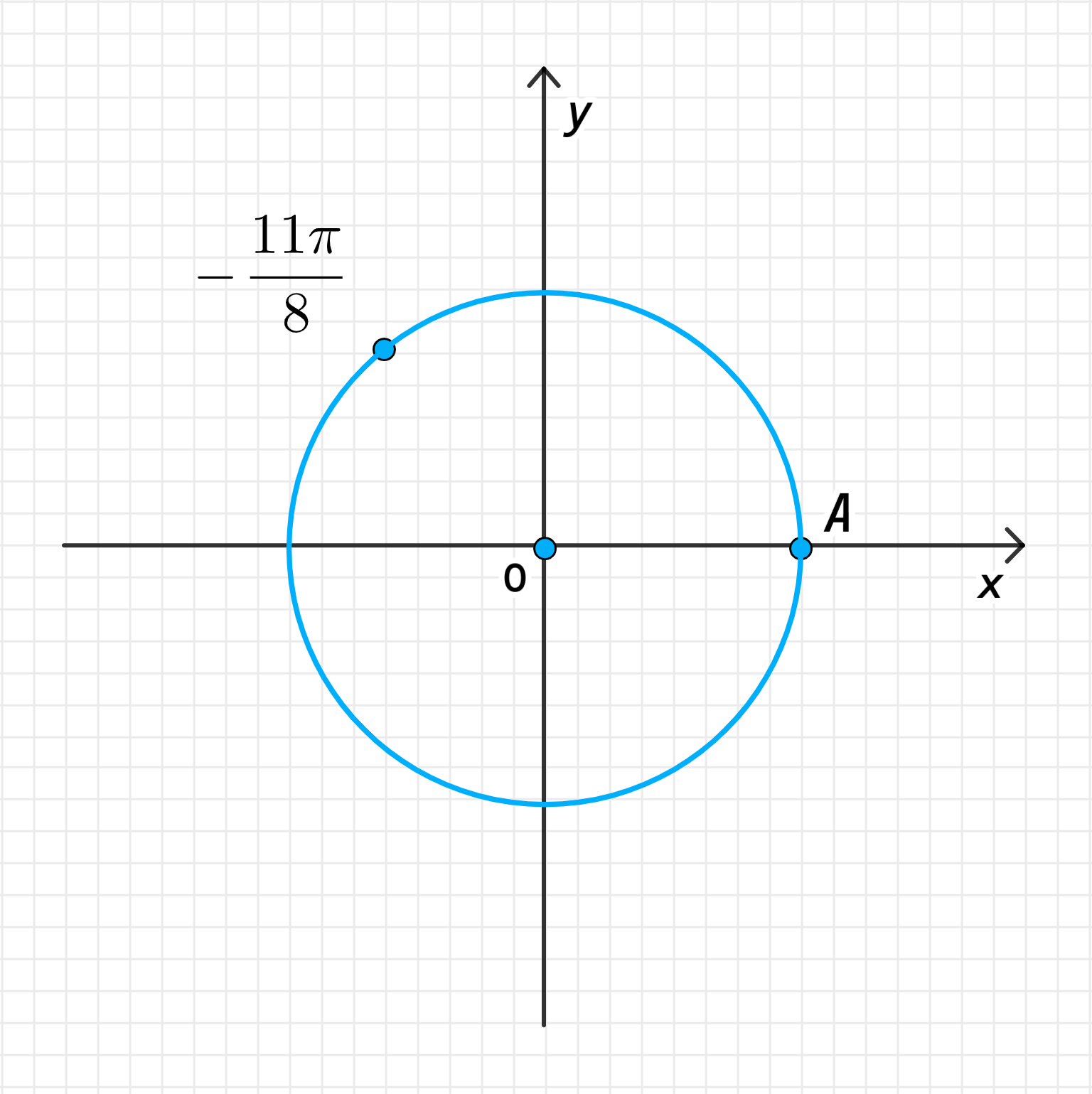
г) Число :
;
Соответствует повороту точки на угол против часовой стрелки;
То есть искомая точка делит дугу в отношении:
На числовой окружности:
а) Число :
- Соответствие числа повороту точки :
Число представляет собой угол, равный 22,5 градуса. Это означает, что точка будет поворачиваться на угол против часовой стрелки от своей исходной позиции. Поскольку меньше, чем угол , это относительно небольшой поворот, и точка окажется на окружности на небольшом расстоянии от своей начальной позиции.
- Деление дуги :
Дуга между точками и соответствует углу радиан (или 90 градусов). Когда точка поворачивается на угол , она делит дугу в отношении:
Это означает, что точка расположена на четвертой части пути между точками и .
- Графическое изображение:
На числовой окружности точка будет находиться на -м пути от точки до точки . Это визуализируется как небольшое смещение точки на угол по окружности.
б) Число :
- Приведение угла к положительному эквиваленту:
Мы имеем отрицательное число , что означает, что точка будет двигаться по часовой стрелке. Чтобы найти эквивалентный положительный угол, добавим (так как полный круг равен ):
Это эквивалентно повороту на угол против часовой стрелки, что позволяет работать с положительным углом.
- Поворот точки на угол :
Поворот точки на угол против часовой стрелки будет происходить на угол чуть больше (то есть чуть больше 45 градусов). Точка переместится по окружности на этот угол.
- Деление дуги :
Дуга соответствует углу радиан (или 90 градусов). Точка делит дугу в отношении:
Это означает, что точка будет находиться на пути от точки до точки .
- Графическое изображение:
На числовой окружности точка будет расположена на -м пути от точки до точки . Это означает, что точка почти достигла точки , но еще не достигла её.
в) Число :
- Приведение числа к эквивалентному углу:
Угол больше, чем , но меньше, чем полный оборот . Мы можем выразить этот угол как сумму двух углов:
Это означает, что угол — это угол, который включает половину окружности () плюс дополнительный угол .
- Поворот точки на угол :
Поворот точки на угол против часовой стрелки будет происходить на небольшой угол, равный , от ее исходной позиции.
- Деление дуги :
Дуга составляет радиан (или 90 градусов). Точка делит дугу в отношении:
Это означает, что точка будет находиться на -м пути от точки до точки .
- Графическое изображение:
На числовой окружности точка будет расположена на -м пути от точки до точки .
г) Число :
- Приведение числа к эквивалентному углу:
Поскольку угол отрицательный, он будет вращаться по часовой стрелке. Чтобы привести его к положительному эквивалентному углу, добавим (или ):
Это означает, что угол эквивалентен углу после полного оборота и дополнительного поворота на угол .
- Поворот точки на угол :
Поворот точки на угол против часовой стрелки переместит точку на угол по окружности, что является небольшим смещением.
- Деление дуги :
Дуга соответствует углу радиан. Точка делит дугу в отношении:
Это означает, что точка будет находиться на -м пути от точки до точки .
- Графическое изображение:
На числовой окружности точка будет расположена на -м пути от точки до точки .