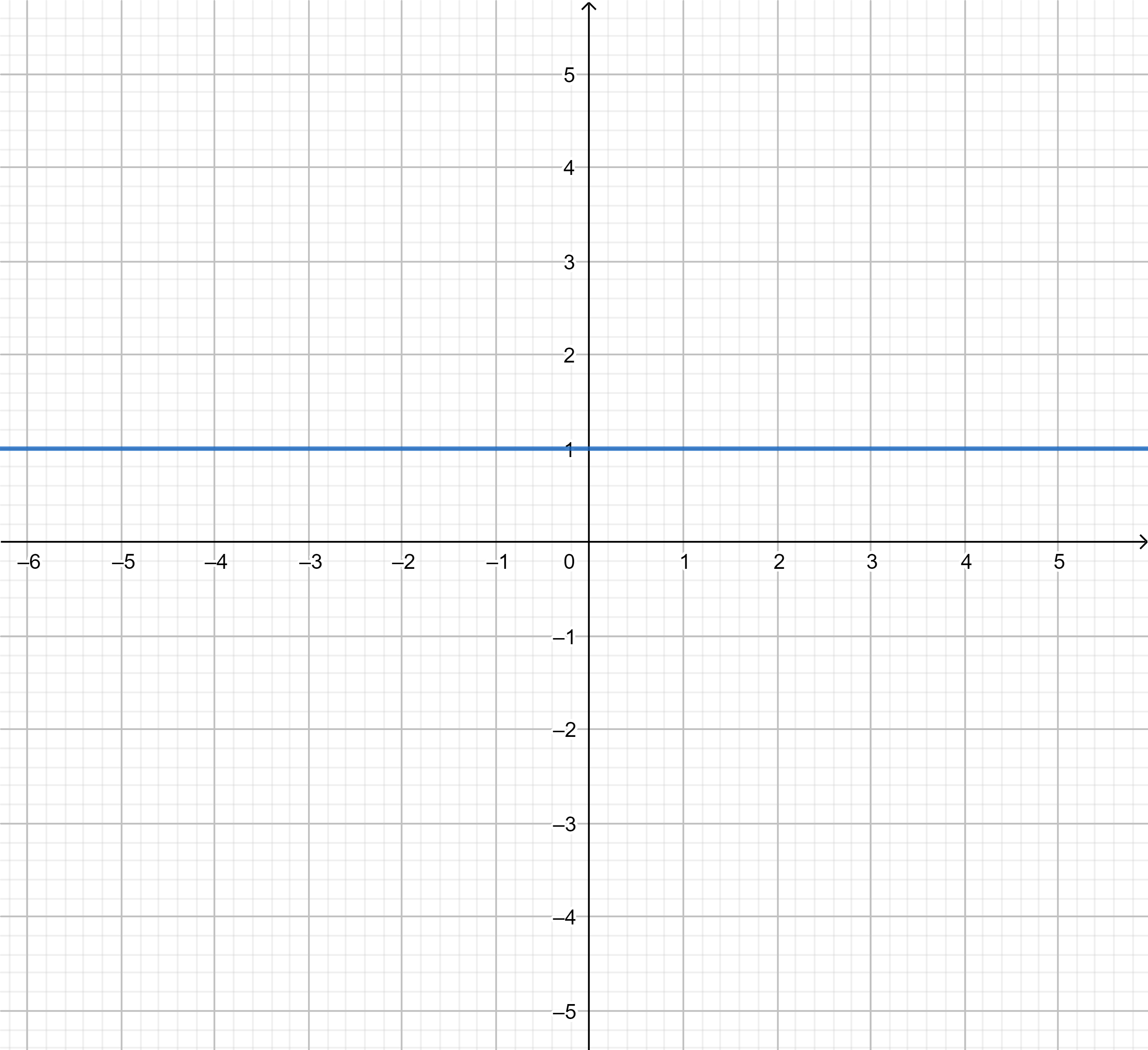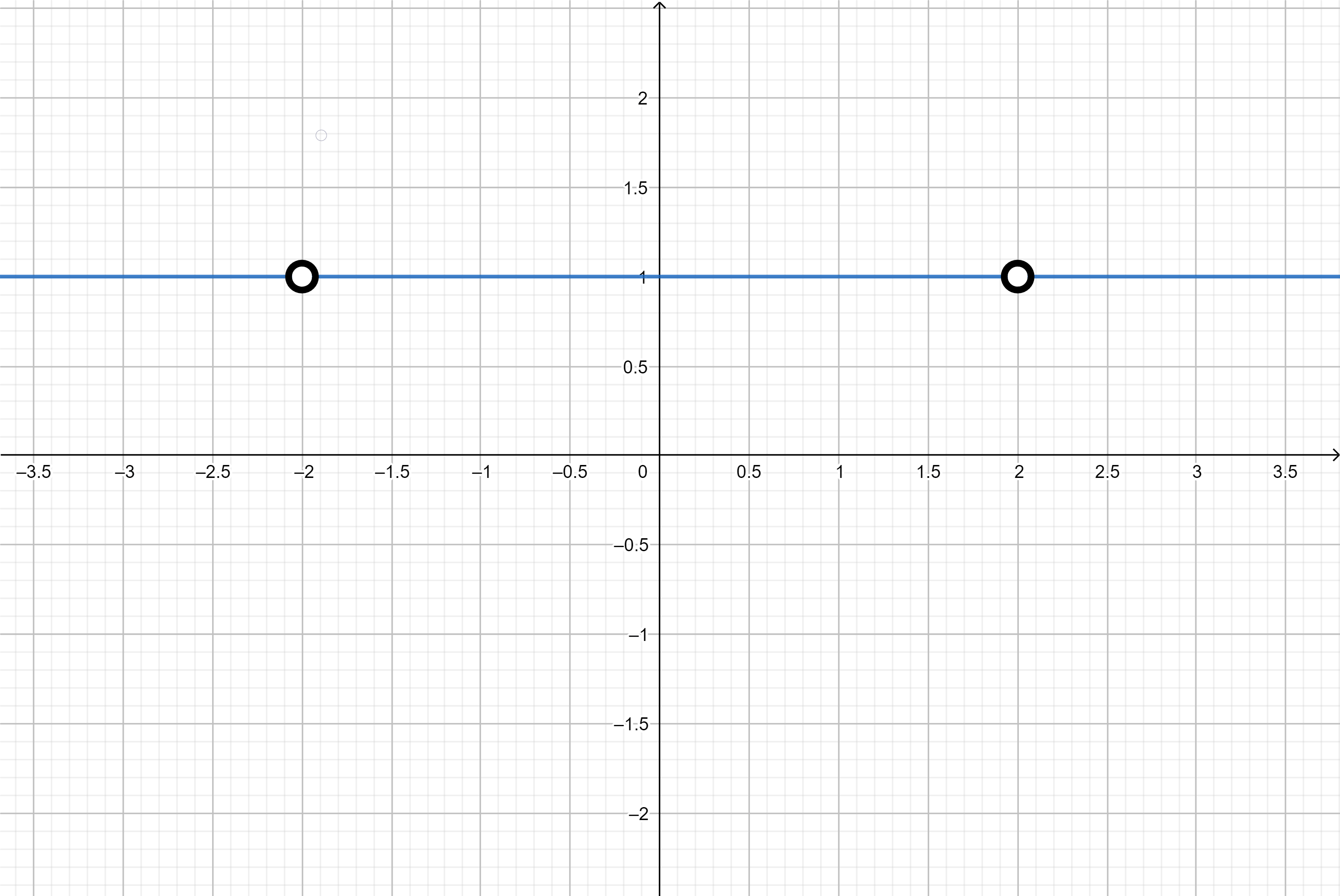ГДЗ по Алгебре 10 Класс Номер 14.34 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \cos^2 x + \sin^2 x = 1$;

б) $y = \cos^2 \frac{1}{x} + \sin^2 \frac{1}{x} = 1$;

в) $y = \sin^2 \sqrt{x} + \cos^2 \sqrt{x} = 1$;

г) $y={\sin }^2\frac{1}{x^2-4}+{\cos }^2\frac{1}{x^2-4}=1$

а) $y = \cos^2 x + \sin^2 x = 1$;

Область определения функции:

$$x \in \mathbb{R};$$

График функции:

б) $y = \cos^2 \frac{1}{x} + \sin^2 \frac{1}{x} = 1$;

Область определения функции:

$$x \neq 0;$$

График функции:

в) $y = \sin^2 \sqrt{x} + \cos^2 \sqrt{x} = 1$;

Область определения функции:

$$x \geq 0;$$

График функции:

г) $y = \sin^2 \frac{1}{x^2 — 4} + \cos^2 \frac{1}{x^2 — 4} = 1$;

Область определения функции:

$$x^2 — 4 \neq 0;$$ $$x^2 \neq 4;$$ $$x \neq \pm 2;$$

График функции:

Рассмотрим каждую часть задачи. В этих заданиях используется основное тригонометрическое тождество:

$$\cos^2 \theta + \sin^2 \theta = 1$$

Часть а) $y = \cos^2 x + \sin^2 x = 1$

Область определения функции:

Функция состоит из выражений $\cos^2 x$ и $\sin^2 x$, которые являются стандартными тригонометрическими функциями. Они определены для всех значений $x$ на множестве действительных чисел $\mathbb{R}$.

Таким образом, область определения функции:

$$x \in \mathbb{R}$$

График функции:

Поскольку выражение $\cos^2 x + \sin^2 x = 1$ всегда истинно для любого значения $x$, то график функции представляет собой горизонтальную прямую, расположенную на уровне $y = 1$ на оси $y$.

График функции:

Эта функция является постоянной (независимой от $x$).

Независимо от значения $x$, результат всегда равен 1.

Точнее, график функции — это горизонтальная прямая, проходящая через точку $(x, 1)$ для всех $x \in \mathbb{R}$.

Часть б) $y = \cos^2 \frac{1}{x} + \sin^2 \frac{1}{x} = 1$

Область определения функции:

Аналогично предыдущей части, выражение $\cos^2 \frac{1}{x} + \sin^2 \frac{1}{x}$ всегда равно 1 для всех $x$, для которых выражения $\cos \frac{1}{x}$ и $\sin \frac{1}{x}$ определены.

Однако, выражения $\cos \frac{1}{x}$ и $\sin \frac{1}{x}$ определены только тогда, когда $x \neq 0$, поскольку деление на ноль (при $x = 0$) невозможно.

Таким образом, область определения функции:

$$x \neq 0$$

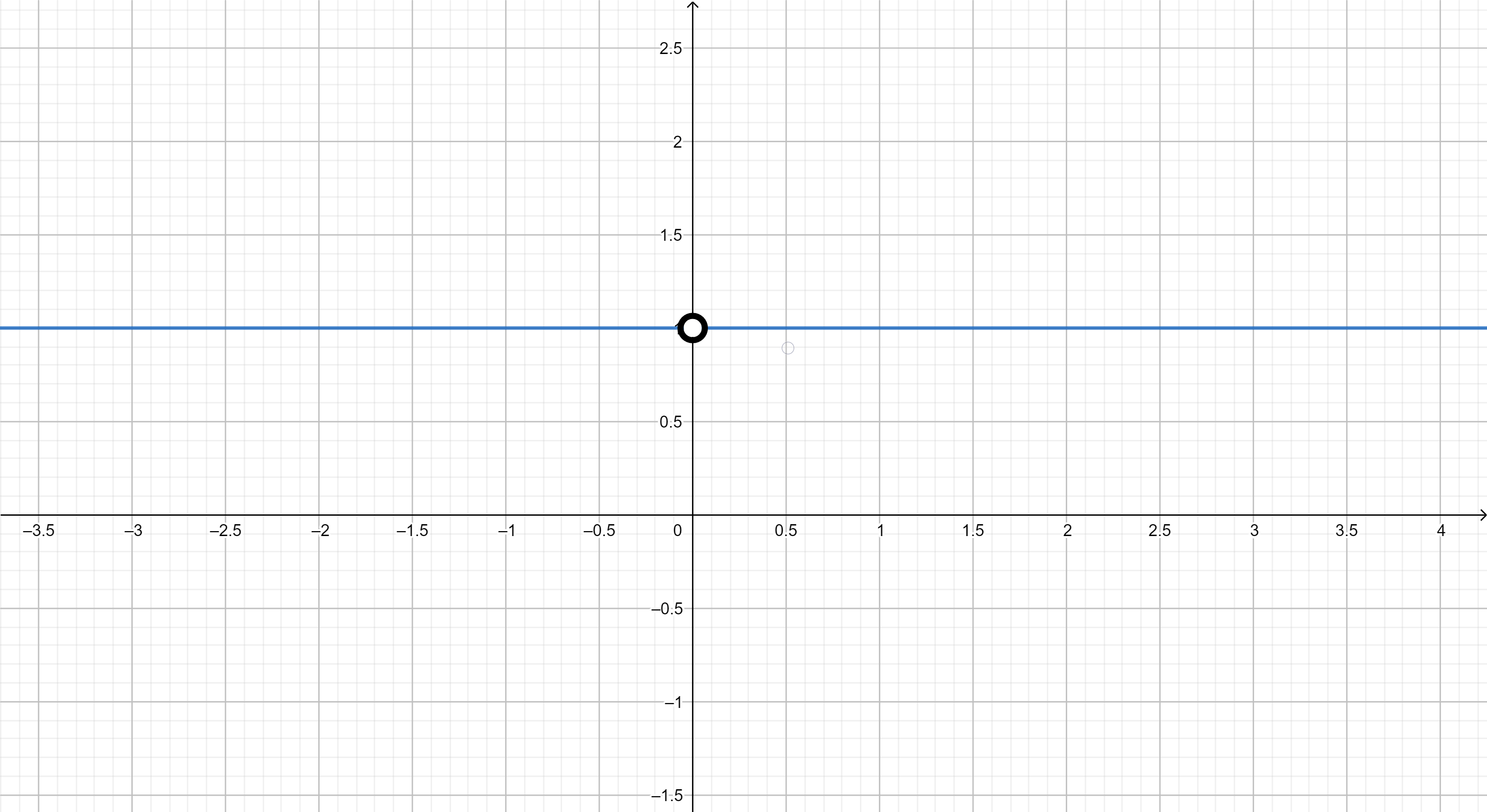
График функции:

Подобно первой части, где использовалось тождество $\cos^2 \theta + \sin^2 \theta = 1$, это тождество верно для всех значений $x$, за исключением $x = 0$. Таким образом, график функции представляет собой горизонтальную прямую на уровне $y = 1$, но с исключением точки $x = 0$, где функция не определена.

График функции:

Точнее, график будет горизонтальной прямой, проходящей через $y = 1$, за исключением точки $x = 0$, где график разрывается.

Часть в) $y = \sin^2 \sqrt{x} + \cos^2 \sqrt{x} = 1$

Область определения функции:

В данном случае функции $\cos^2 \sqrt{x}$ и $\sin^2 \sqrt{x}$ определены только тогда, когда $\sqrt{x}$ существует, а это возможно при $x \geq 0$, потому что квадратный корень из отрицательного числа не существует в области действительных чисел.

Таким образом, область определения функции:

$$x \geq 0$$

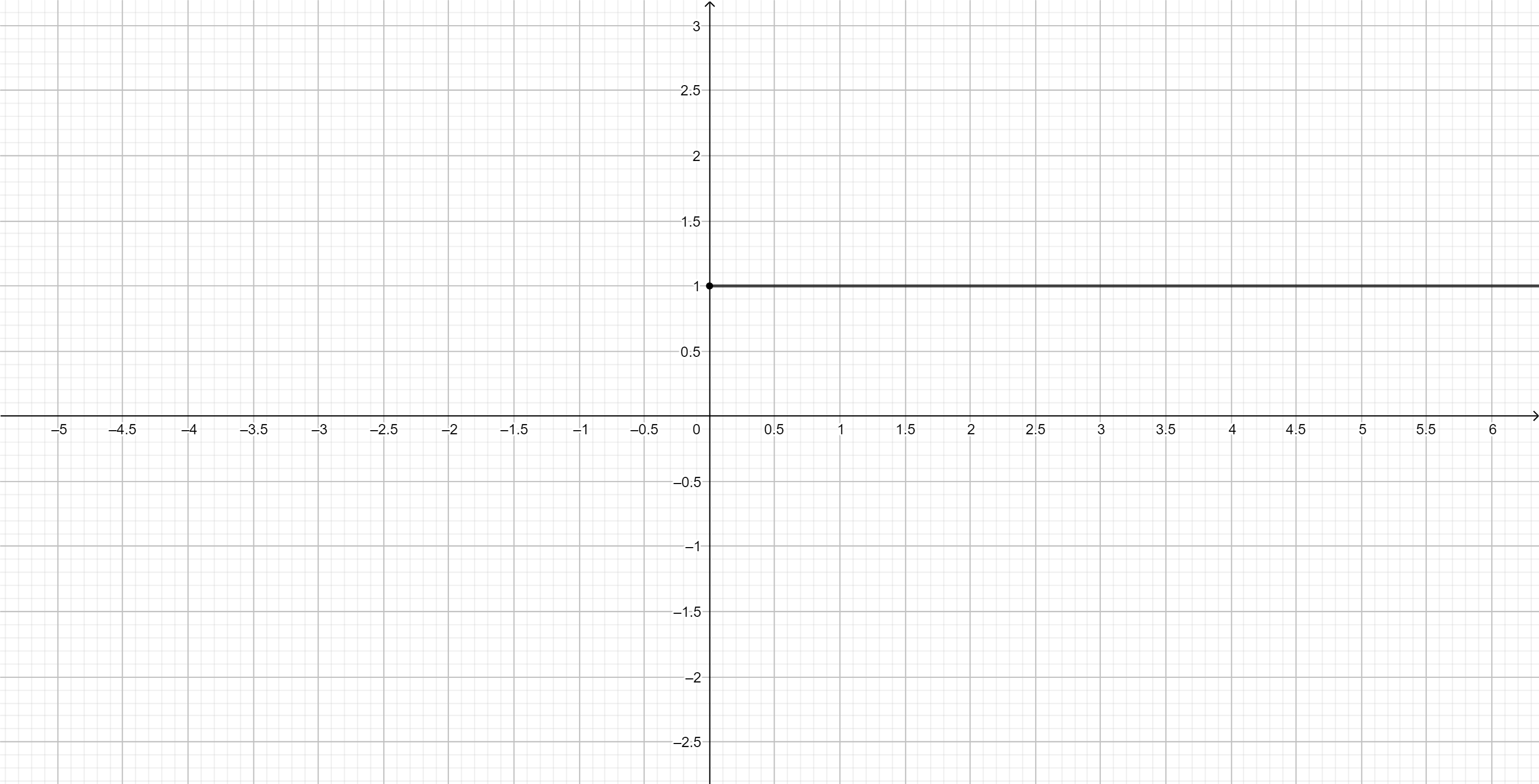
График функции:

Как и в предыдущих частях, выражение $\sin^2 \theta + \cos^2 \theta = 1$ выполняется всегда для любого значения $\theta$. Здесь же $\theta = \sqrt{x}$, и, поскольку эта функция всегда равна 1 при любом $x \geq 0$, график функции будет горизонтальной прямой на уровне $y = 1$, но только для $x \geq 0$.

Таким образом, график функции:

Горизонтальная прямая, проходящая через $y = 1$.

Прямая начинается с точки $x = 0$ и продолжается вправо для всех $x \geq 0$.

Часть г) $y = \sin^2 \frac{1}{x^2 — 4} + \cos^2 \frac{1}{x^2 — 4} = 1$

Область определения функции:

Для того чтобы выражения $\cos^2 \frac{1}{x^2 — 4}$ и $\sin^2 \frac{1}{x^2 — 4}$ были определены, необходимо, чтобы знаменатель $x^2 — 4$ не равнялся нулю. То есть:

$$x^2 — 4 \neq 0$$

Решая это неравенство:

$$x^2 \neq 4$$ $$x \neq \pm 2$$

Таким образом, область определения функции:

$$x \neq \pm 2$$

График функции:

Точно так же, как и в других частях, $\sin^2 \theta + \cos^2 \theta = 1$ всегда верно для всех значений $\theta$, где $\theta = \frac{1}{x^2 — 4}$. Однако, при $x = \pm 2$ выражение $x^2 — 4$ обращается в ноль, что делает функцию не определенной в этих точках.

График функции:

Таким образом, график функции представляет собой горизонтальную прямую на уровне $y = 1$, за исключением точек $x = 2$ и $x = -2$, где функция не определена.

График будет похож на прямую $y = 1$, но с разрывами в точках $x = \pm 2$, где функция не существует.