ГДЗ по Алгебре 10 Класс Номер 15.11 Профильный Уровень Мордкович — Подробные Ответы

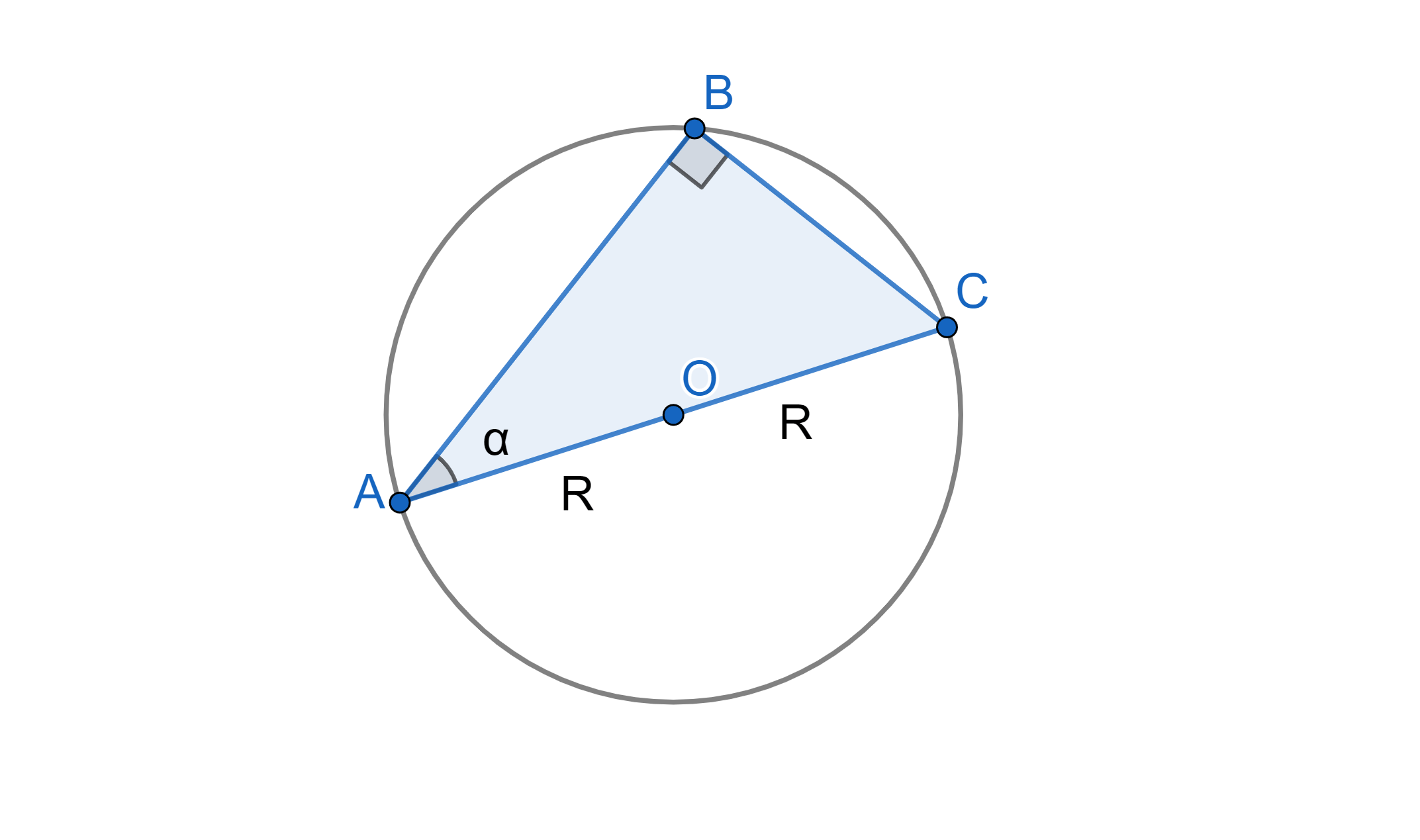
Хорда AB образует с диаметром AC окружности угол а°. Найдите длину хорды AB, если радиус окружности равен R.

Хорда $AB$ образует с диаметром $AC$ окружности угол $a^\circ$;

Найти длину хорды $AB$, если радиус окружности равен $R$;

Отобразим условие задачи:

Так как $AC$ — диаметр окружности:
$AC = AO + OC = R + R = 2R;$

Угол $B$ опирается на диаметр окружности, значит:
$\angle ABC = 90^\circ;$

Треугольник $ABC$ прямоугольный, следовательно:
$\cos a = \frac{\overline{AB}}{\overline{AC}},$
$AB = AC \cdot \cos a = 2R \cdot \cos a;$

Ответ: $2R \cdot \cos a$.

Дано, что хорда $AB$ окружности образует с диаметром $AC$ угол $a^\circ$, и требуется найти длину хорды $AB$, если радиус окружности равен $R$.

1. Построение и обозначения

• Окружность имеет центр $O$ и радиус $R$.
• Хорда $AB$ пересекает окружность в точке $B$, и угол $\angle ABC = a^\circ$ образуется между хордами $AB$ и диаметром $AC$.
• Диаметр $AC$ — это отрезок, который соединяет точки $A$ и $C$, проходя через центр окружности $O$.

Поставим точку $O$ в центр окружности, а точку $A$ — на окружности. Диаметр $AC$ — это отрезок, который проходит через центр окружности $O$, то есть $A$ и $C$ лежат на противоположных концах диаметра.

2. Основные геометрические соотношения

• Поскольку $AC$ — диаметр окружности, длина этого отрезка равна $2R$, где $R$ — радиус окружности. То есть:

  $$AC = 2R$$

• Угол $\angle ABC$ между хордами $AB$ и $AC$ равен $90^\circ$, поскольку по теореме о хорде, которая опирается на диаметр окружности, угол между ней и диаметром всегда прямой (это является следствием из теоремы о полукруге). Поэтому:

  $$\angle ABC = 90^\circ$$

3. Применение теоремы о прямоугольном треугольнике

Теперь мы видим, что треугольник $ABC$ является прямоугольным, так как $\angle ABC = 90^\circ$. В таком треугольнике мы можем применить основные тригонометрические соотношения.

Согласно определению косинуса в прямоугольном треугольнике, для угла $a$ (где $a^\circ$ — это угол между хордами $AB$ и $AC$) справедливо следующее отношение:

$$\cos a = \frac{\overline{AB}}{\overline{AC}}$$

где:

• $\overline{AB}$ — длина хорды $AB$,
• $\overline{AC}$ — длина диаметра окружности $AC$.

Таким образом, из этого выражения можно выразить длину хорды $AB$ как:

$$\overline{AB} = \overline{AC} \cdot \cos a$$

4. Подстановка значений

Из предыдущих шагов мы знаем, что длина диаметра $AC = 2R$. Подставим это значение в уравнение:

$$\overline{AB} = 2R \cdot \cos a$$

Ответ

Длина хорды $AB$ равна $2R \cdot \cos a$.