ГДЗ по Алгебре 10 Класс Номер 15.12 Профильный Уровень Мордкович — Подробные Ответы

Докажите, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Доказать, что площадь выпуклого четырехугольника равна половине произведения длин его диагоналей на синус угла между ними;

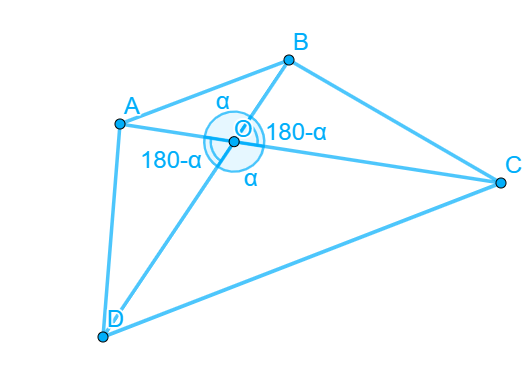
Пусть дан четырехугольник $ABCD$, диагонали $AC$ и $BD$ которого пересекаются в точке $O$, а острый угол $AOD$ между ними равен $\alpha$:

Выведем тождество:

$$\sin(180^\circ — \alpha) = \sin(\pi — \alpha) = -\sin(-\alpha) = \sin \alpha;$$

По теореме о площади треугольника:

$$S_{AOB} = \frac{1}{2} \cdot AO \cdot BO \cdot \sin(180^\circ — \alpha) = \frac{1}{2} AO \cdot BO \cdot \sin \alpha;$$ $$S_{BOC} = \frac{1}{2} \cdot BO \cdot OC \cdot \sin \alpha;$$ $$S_{COD} = \frac{1}{2} \cdot CO \cdot OD \cdot \sin(180^\circ — \alpha) = \frac{1}{2} CO \cdot OD \cdot \sin \alpha;$$ $$S_{AOD} = \frac{1}{2} \cdot DO \cdot AO \cdot \sin \alpha;$$

Площадь четырехугольника:

$$S_{ABCD} = S_{AOB} + S_{BOC} + S_{COD} + S_{AOD};$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot (AO \cdot BO + BO \cdot OC + CO \cdot OD + DO \cdot AO);$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot \big( BO(AO + OC) + OD(AO + OC) \big);$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot (AO + OC) \cdot (BO + OD);$$ $$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot AC \cdot BD;$$

Что и требовалось доказать.

Шаг 1. Введение в задачу

Пусть дан выпуклый четырехугольник $ABCD$, диагонали которого $AC$ и $BD$ пересекаются в точке $O$. Обозначим угол между диагоналями, образованный в точке их пересечения, как $\alpha$ — это угол $AOD$.

Нужно доказать, что площадь этого четырехугольника $S_{ABCD}$ равна половине произведения длин диагоналей $AC$ и $BD$ на синус угла между ними $\alpha$. Формально, нужно доказать, что:

$$S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD \cdot \sin \alpha$$

Шаг 2. Разбиение четырехугольника на треугольники

Площадь четырехугольника $ABCD$ можно выразить через сумму площадей четырех треугольников, которые образуются точкой пересечения диагоналей $O$. Эти треугольники — $AOB$, $BOC$, $COD$, $AOD$.

Площадь каждого треугольника можно выразить с помощью формулы площади треугольника через две стороны и угол между ними.

Шаг 3. Вывод формул для площади каждого из треугольников

Для того чтобы вычислить площади треугольников, воспользуемся формулой для площади треугольника через две стороны и угол между ними:

$$S = \frac{1}{2} \cdot a \cdot b \cdot \sin(\theta)$$

где $a$ и $b$ — это длины сторон треугольника, а $\theta$ — угол между ними.

Площадь треугольника $AOB$:

$$S_{AOB} = \frac{1}{2} \cdot AO \cdot BO \cdot \sin(180^\circ — \alpha)$$

Так как $\sin(180^\circ — \alpha) = \sin \alpha$, получаем:

$$S_{AOB} = \frac{1}{2} \cdot AO \cdot BO \cdot \sin \alpha$$

Площадь треугольника $BOC$:

$$S_{BOC} = \frac{1}{2} \cdot BO \cdot OC \cdot \sin \alpha$$

Площадь треугольника $COD$:

$$S_{COD} = \frac{1}{2} \cdot CO \cdot OD \cdot \sin(180^\circ — \alpha)$$

Так как $\sin(180^\circ — \alpha) = \sin \alpha$, получаем:

$$S_{COD} = \frac{1}{2} \cdot CO \cdot OD \cdot \sin \alpha$$

Площадь треугольника $AOD$:

$$S_{AOD} = \frac{1}{2} \cdot DO \cdot AO \cdot \sin \alpha$$

Шаг 4. Общая площадь четырехугольника

Теперь, когда мы нашли площади всех четырёх треугольников, сложим их для получения площади всего четырехугольника $ABCD$:

$$S_{ABCD} = S_{AOB} + S_{BOC} + S_{COD} + S_{AOD}$$

Подставим выражения для каждой из площадей:

$$S_{ABCD} = \frac{1}{2} \cdot AO \cdot BO \cdot \sin \alpha + \frac{1}{2} \cdot BO \cdot OC \cdot \sin \alpha + \frac{1}{2} \cdot CO \cdot OD \cdot \sin \alpha + \frac{1}{2} \cdot DO \cdot AO \cdot \sin \alpha$$

Теперь вынесем общий множитель $\frac{1}{2} \cdot \sin \alpha$:

$$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot \left( AO \cdot BO + BO \cdot OC + CO \cdot OD + DO \cdot AO \right)$$

Шаг 5. Упрощение выражения

Теперь сгруппируем одинаковые множители:

$$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot \left( BO(AO + OC) + OD(AO + OC) \right)$$

Вынесем $AO + OC$ за скобки:

$$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot (AO + OC) \cdot (BO + OD)$$

Так как $AO + OC = AC$ и $BO + OD = BD$ — это длины диагоналей четырехугольника $AC$ и $BD$, то получаем:

$$S_{ABCD} = \frac{1}{2} \sin \alpha \cdot AC \cdot BD$$

Шаг 6. Заключение

Таким образом, мы доказали, что площадь выпуклого четырехугольника $ABCD$ равна половине произведения длин его диагоналей на синус угла между ними:

$$S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD \cdot \sin \alpha$$

Что и требовалось доказать.