ГДЗ по Алгебре 10 Класс Номер 15.14 Профильный Уровень Мордкович — Подробные Ответы

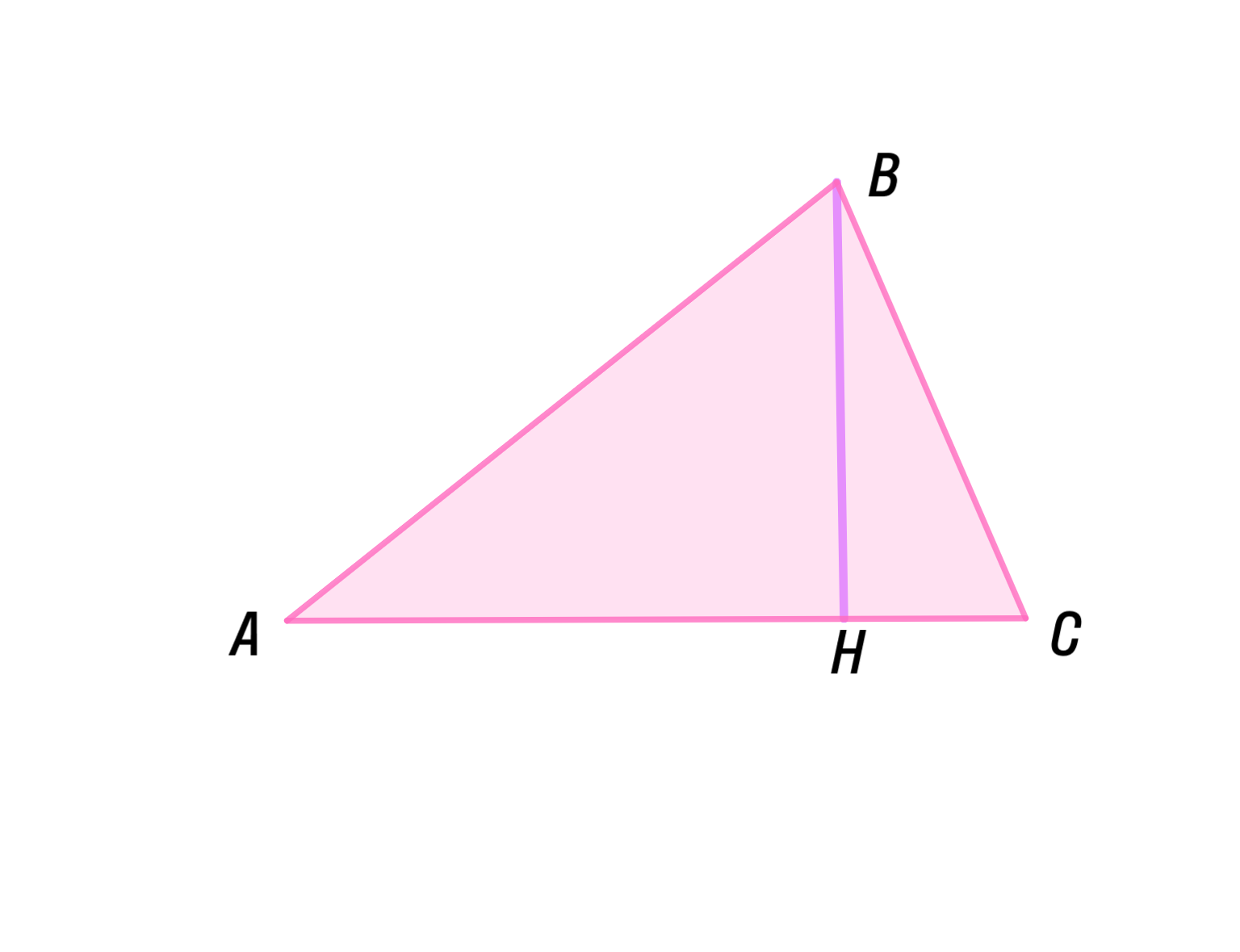
Высота треугольника равна 5 см, а углы, прилегающие к основанию, равны 60° и 45°. Найдите площадь треугольника.

В ΔABC известно, что высота $AH = 5$ см, $\angle A = 45^\circ$, $\angle C = 60^\circ$.
Найти площадь ΔABC.

Решение:

Отобразим условие задачи:

• Высота $AH = 5$ см
• $\angle A = 45^\circ$
• $\angle C = 60^\circ$

Радианные меры углов:

$$\angle A = 45^\circ = \frac{\pi \cdot 45^\circ}{180^\circ} = \frac{9\pi}{36} = \frac{\pi}{4};$$ $$\angle C = 60^\circ = \frac{\pi \cdot 60^\circ}{180^\circ} = \frac{6\pi}{18} = \frac{\pi}{3};$$

Рассмотрим прямоугольный ΔCBH:

$$\text{ctg } \angle C = \frac{CH}{BH};$$ $$CH = BH \cdot \text{ctg } \angle C = 5 \cdot \text{ctg } \frac{\pi}{3} = 5 \cdot \frac{1}{\sqrt{3}} = \frac{5\sqrt{3}}{3} \text{ см};$$

Рассмотрим прямоугольный ΔABH:

$$\text{ctg } \angle A = \frac{AH}{BH};$$ $$AH = BH \cdot \text{ctg } \angle A = 5 \cdot \text{ctg } \frac{\pi}{4} = 5 \cdot 1 = 5 \text{ см};$$

Длина стороны AC:

$$AC = AH + HC = 5 + \frac{5\sqrt{3}}{3} = \frac{15 + 5\sqrt{3}}{3} = \frac{5(3 + \sqrt{3})}{3} \text{ см};$$

Площадь треугольника ABC:

$$S_{\Delta ABC} = \frac{1}{2} \cdot AC \cdot BH = \frac{1}{2} \cdot \frac{5(3 + \sqrt{3})}{3} \cdot 5 = \frac{25(3 + 3\sqrt{3})}{6} \text{ см}^2;$$

Ответ:

$$S_{\Delta ABC} = \frac{25(3 + 3\sqrt{3})}{6} \text{ см}^2.$$

В ΔABC известно, что высота $AH = 5$ см, $\angle A = 45^\circ$, $\angle C = 60^\circ$.
Найти площадь ΔABC.

Даны:

• Высота $AH = 5$ см.
• Угол $\angle A = 45^\circ$.
• Угол $\angle C = 60^\circ$.

Нужно найти площадь треугольника $ABC$. Для этого мы будем использовать геометрические и тригонометрические методы. Нам нужно будет использовать высоту, тригонометрические функции для вычисления сторон и площади.

Преобразование углов в радианы:

Чтобы использовать тригонометрические функции, важно перевести углы в радианы, так как в таких единицах работают тригонометрические функции.

Перевод углов в радианы:

• Для угла $\angle A = 45^\circ$:

  $$\angle A = 45^\circ = \frac{\pi \cdot 45^\circ}{180^\circ} = \frac{\pi}{4} \, \text{радиан}.$$

• Для угла $\angle C = 60^\circ$:

  $$\angle C = 60^\circ = \frac{\pi \cdot 60^\circ}{180^\circ} = \frac{\pi}{3} \, \text{радиан}.$$

Используем прямоугольный треугольник $CBH$:

Рассмотрим прямоугольный треугольник $CBH$, где $H$ — это основание высоты $AH$, проведенной из вершины $A$ на сторону $BC$. В этом треугольнике угол $C = 60^\circ$, а гипотенуза $BC$ является стороной нашего исходного треугольника.

Воспользуемся тригонометрической функцией $\text{ctg}$, чтобы найти длину отрезка $CH$ на основании высоты. Напоминаем, что $\text{ctg}$ угла в прямоугольном треугольнике определяет отношение прилежащего катета к противолежащему.

Для угла $\angle C = 60^\circ$:

$$\text{ctg } \angle C = \frac{CH}{BH}.$$

Из этого выражения можем выразить $CH$:

$$CH = BH \cdot \text{ctg } \angle C.$$

Известно, что $\text{ctg } 60^\circ = \frac{1}{\sqrt{3}}$, поэтому:

$$CH = 5 \cdot \frac{1}{\sqrt{3}} = \frac{5\sqrt{3}}{3} \, \text{см}.$$

Используем прямоугольный треугольник $ABH$:

Рассмотрим теперь прямоугольный треугольник $ABH$, где $H$ — это основание высоты $AH$, а угол $A = 45^\circ$. В этом треугольнике гипотенуза $AB$ является стороной исходного треугольника $ABC$.

Для нахождения $AH$ из треугольника $ABH$ воспользуемся тригонометрической функцией $\text{ctg}$, так как $\text{ctg}$ угла равна отношению прилежащего катета к противолежащему:

$$\text{ctg } \angle A = \frac{AH}{BH}.$$

Таким образом, мы получаем:

$$AH = BH \cdot \text{ctg } \angle A.$$

Поскольку $\text{ctg } 45^\circ = 1$, то:

$$AH = 5 \cdot 1 = 5 \, \text{см}.$$

Длина стороны $AC$:

Сторона $AC$ является суммой двух отрезков $AH$ и $HC$, то есть:

$$AC = AH + HC.$$

Подставим известные значения:

$$AC = 5 + \frac{5\sqrt{3}}{3}.$$

Приводим к общему знаменателю:

$$AC = \frac{15}{3} + \frac{5\sqrt{3}}{3} = \frac{15 + 5\sqrt{3}}{3}.$$

Это и есть длина стороны $AC$:

$$AC = \frac{5(3 + \sqrt{3})}{3} \, \text{см}.$$

Площадь треугольника $ABC$:

Площадь треугольника $ABC$ можно вычислить по формуле площади треугольника через основание и высоту:

$$S_{\Delta ABC} = \frac{1}{2} \cdot AC \cdot BH.$$

Подставляем значения $AC = \frac{5(3 + \sqrt{3})}{3}$ и $BH = 5$:

$$S_{\Delta ABC} = \frac{1}{2} \cdot \frac{5(3 + \sqrt{3})}{3} \cdot 5.$$

Упростим выражение:

$$S_{\Delta ABC} = \frac{25(3 + \sqrt{3})}{6}.$$

Это и есть площадь треугольника $ABC$.

Ответ:

$$S_{\Delta ABC} = \frac{25(3 + 3\sqrt{3})}{6} \text{ см}^2.$$