ГДЗ по Алгебре 10 Класс Номер 15.15 Профильный Уровень Мордкович — Подробные Ответы

Использовав геометрические соображения, вычислите:

а) sin 15° и cos 15°;

б) sin 22,5° и cos 22,5°.

а) Найти sin 15° и cos 15°;

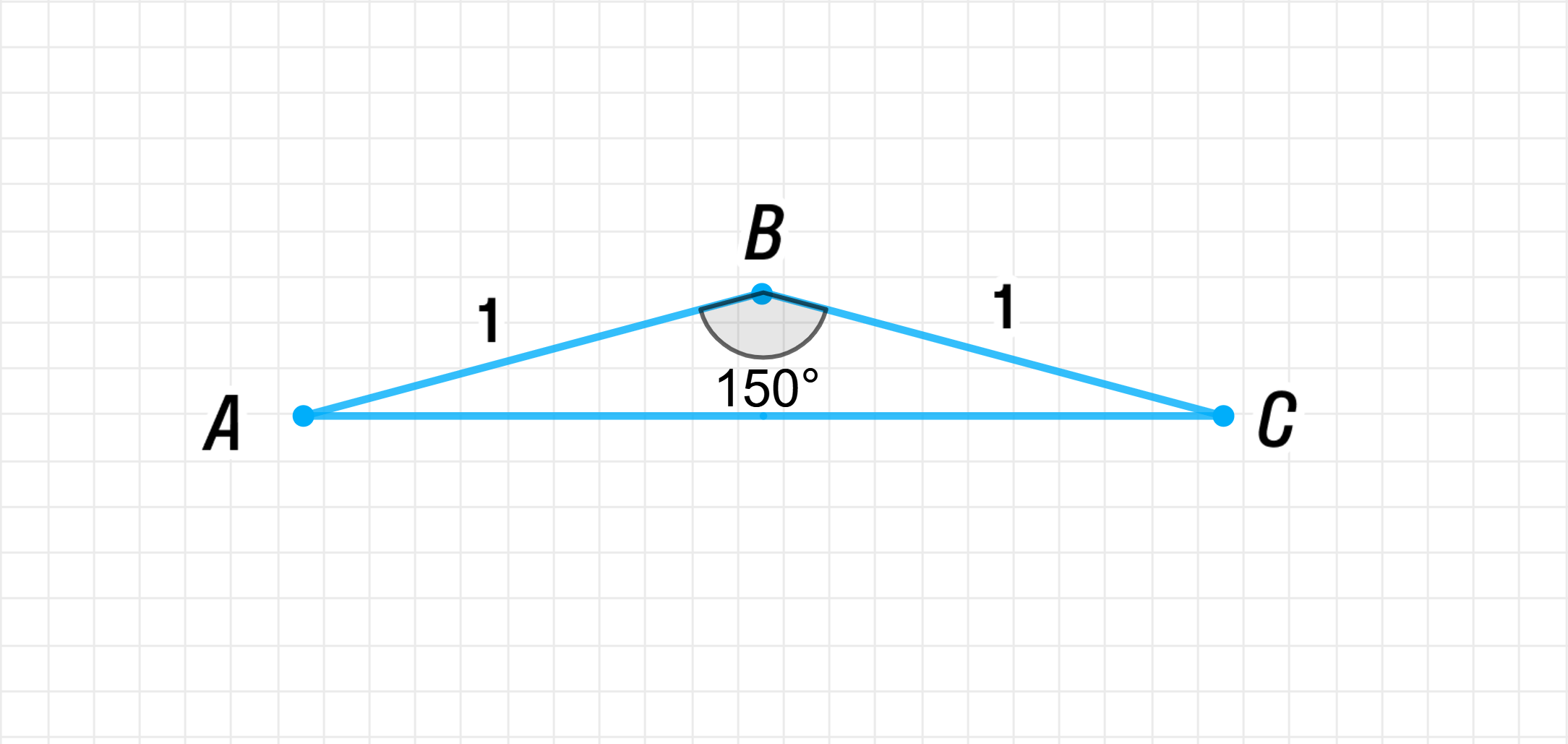
Построим равнобедренный треугольник $\triangle ABC$, у которого:

• $\angle A = \angle C = 15^\circ$;
• $AB = BC = 1$;

По теореме о сумме углов треугольника:

$$\angle B = 180^\circ — \angle A — \angle C = 180^\circ — 15^\circ — 15^\circ = 150^\circ;$$ $$\angle B = 150^\circ = \frac{\pi \cdot 150^\circ}{180^\circ} = \frac{15\pi}{18} = \frac{5\pi}{6};$$

По теореме косинусов:

$$AC = \sqrt{AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos \angle B};$$ $$AC = \sqrt{1^2 + 1^2 — 2 \cdot 1 \cdot 1 \cdot \cos \frac{5\pi}{6}} = \sqrt{1 + 1 — 2 \cdot \left(-\frac{\sqrt{3}}{2}\right)} = \sqrt{2 + \sqrt{3}};$$

По теореме синусов:

$$\frac{AB}{\sin \angle C} = \frac{AC}{\sin \angle B} \Rightarrow \frac{1}{\sin 15^\circ} = \frac{\sqrt{2 + \sqrt{3}}}{\sin \frac{5\pi}{6}};$$ $$\sin 15^\circ = \frac{\sin \angle B}{\sqrt{2 + \sqrt{3}}} = \frac{\sin \frac{5\pi}{6}}{\sqrt{2 + \sqrt{3}}} = \frac{\frac{1}{2}}{\sqrt{2 + \sqrt{3}}} = \frac{1}{2\sqrt{2 + \sqrt{3}}};$$ $$\sin 15^\circ = \frac{\sqrt{2}}{2\sqrt{3} + 2\sqrt{3} + 1} = \frac{\sqrt{2}}{2\sqrt{(\sqrt{3} + 1)^2}} = \frac{\sqrt{2}}{2(\sqrt{3} + 1)};$$ $$\sin 15^\circ = \frac{\sqrt{2} \cdot (\sqrt{3} — 1)}{2 \cdot (\sqrt{3} + 1)(\sqrt{3} — 1)} = \frac{\sqrt{6} — \sqrt{2}}{2(3 — 1)} = \frac{\sqrt{6} — \sqrt{2}}{4};$$

Число $15^\circ$ принадлежит первой четверти, значит:

$$\cos 15^\circ = +\sqrt{1 — \sin^2 15^\circ} = \sqrt{1 — \left(\frac{\sqrt{6} — \sqrt{2}}{4}\right)^2} = \sqrt{\frac{16 — (6 — 2\sqrt{12} + 2)}{16}};$$ $$\cos 15^\circ = \sqrt{\frac{8 + 2\sqrt{12}}{16}} = \sqrt{\frac{6 + 2\sqrt{12} + 2}{16}} = \sqrt{\frac{(\sqrt{6} + \sqrt{2})^2}{16}} = \frac{\sqrt{6} + \sqrt{2}}{4};$$

Ответ: $\sin 15^\circ = \frac{\sqrt{6} — \sqrt{2}}{4}; \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}$.

б) Найти sin 22,5° и cos 22,5°;

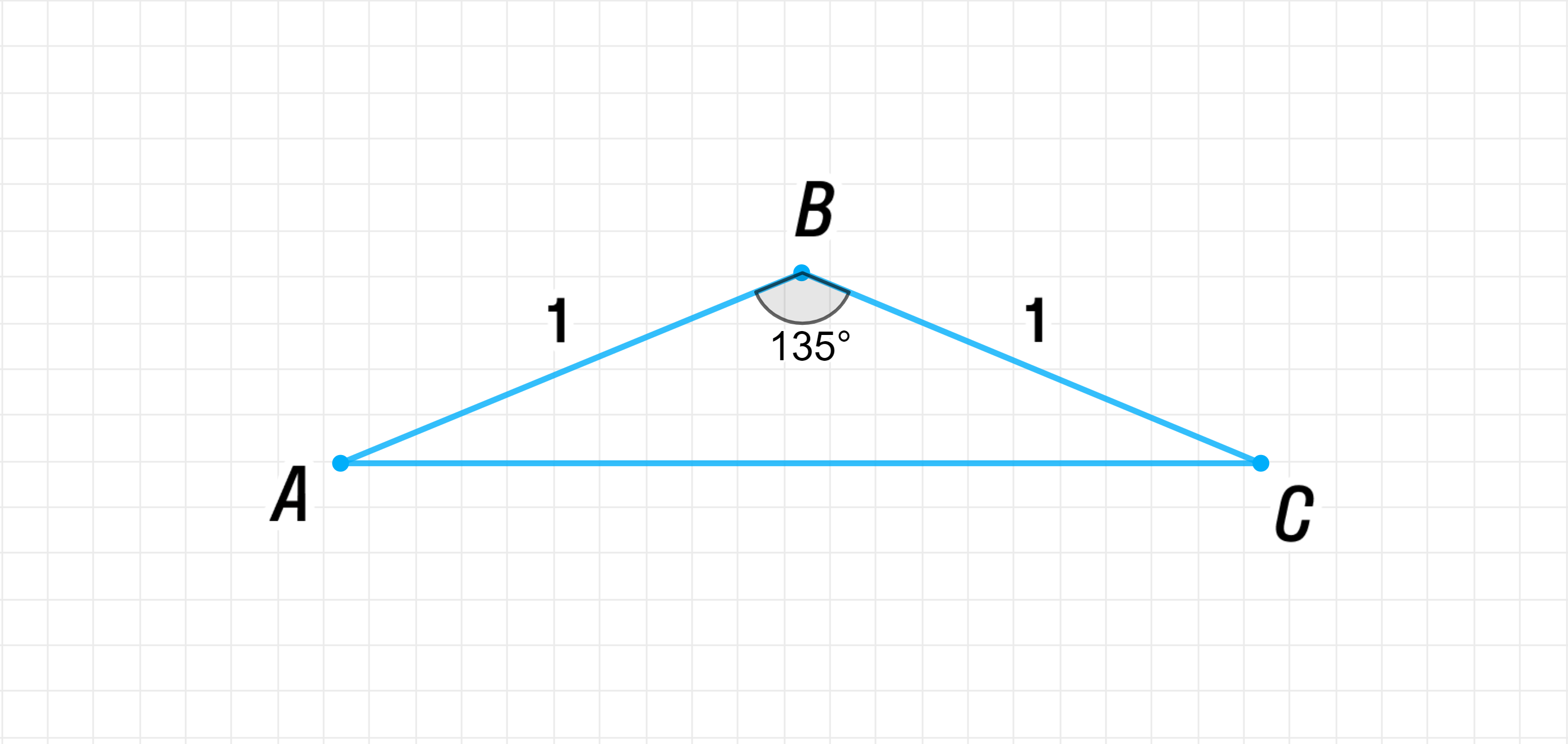
Построим равнобедренный треугольник $\triangle ABC$, у которого:

• $\angle A = \angle C = 22.5^\circ$;
• $AB = BC = 1$;

По теореме о сумме углов треугольника:

$$\angle B = 180^\circ — \angle A — \angle C = 180^\circ — 22.5^\circ — 22.5^\circ = 135^\circ;$$ $$\angle B = 135^\circ = \frac{\pi \cdot 135^\circ}{180^\circ} = \frac{27\pi}{36} = \frac{3\pi}{4};$$

По теореме косинусов:

$$AC = \sqrt{AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos \angle B};$$ $$AC = \sqrt{1^2 + 1^2 — 2 \cdot 1 \cdot 1 \cdot \cos \frac{3\pi}{4}} = \sqrt{1 + 1 — 2 \cdot \left(-\frac{\sqrt{2}}{2}\right)} = \sqrt{2 + \sqrt{2}};$$

По теореме синусов:

$$\frac{AB}{\sin \angle C} = \frac{AC}{\sin \angle B} \Rightarrow \frac{1}{\sin 22.5^\circ} = \frac{\sqrt{2 + \sqrt{2}}}{\sin \frac{3\pi}{4}};$$ $$\sin 22.5^\circ = \frac{\sin \angle B}{\sqrt{2 + \sqrt{2}}} = \frac{\sin \frac{3\pi}{4}}{\sqrt{2 + \sqrt{2}}} = \frac{\frac{\sqrt{2}}{2}}{\sqrt{2 + \sqrt{2}}} = \frac{\sqrt{2}}{2\sqrt{2 + \sqrt{2}}};$$ $$\sin 22.5^\circ = \frac{\sqrt{2} \cdot \sqrt{2} — \sqrt{2}}{2 \cdot \sqrt{4 — 2}} = \frac{\sqrt{2} \cdot \sqrt{2 — \sqrt{2}}}{2 \cdot \sqrt{2}(2 — \sqrt{2})} = \frac{\sqrt{2 — \sqrt{2}}}{2};$$

Число $22.5^\circ$ принадлежит первой четверти, значит:

$$\cos 22.5^\circ = +\sqrt{1 — \sin^2 22.5^\circ} = \sqrt{1 — \left(\frac{\sqrt{2 — \sqrt{2}}}{2}\right)^2} = \sqrt{\frac{4 — (2 — \sqrt{2})}{4}};$$ $$\cos 22.5^\circ = \sqrt{\frac{2 + \sqrt{2}}{4}} = \frac{\sqrt{2 + \sqrt{2}}}{2};$$

Ответ: $\sin 22.5^\circ = \frac{\sqrt{2 — \sqrt{2}}}{2}; \cos 22.5^\circ = \frac{\sqrt{2 + \sqrt{2}}}{2}$.

а) Найти sin 15° и cos 15°;

Построим равнобедренный треугольник $\triangle ABC$, у которого:

• $\angle A = \angle C = 15^\circ$;
• $AB = BC = 1$.

Этот треугольник равнобедренный, значит, его два угла $\angle A$ и $\angle C$ равны, а стороны $AB$ и $BC$ тоже равны. Нам нужно найти значения $\sin 15^\circ$ и $\cos 15^\circ$, используя этот треугольник.

Вычислим угол $\angle B$:
Сначала находим угол $\angle B$ с помощью теоремы о сумме углов в треугольнике:

$$\angle B = 180^\circ — \angle A — \angle C = 180^\circ — 15^\circ — 15^\circ = 150^\circ.$$

Переводим угол в радианы:

$$\angle B = 150^\circ = \frac{\pi \cdot 150^\circ}{180^\circ} = \frac{15\pi}{18} = \frac{5\pi}{6}.$$

Применим теорему косинусов для нахождения стороны $AC$:
По теореме косинусов в треугольнике $ABC$, где $AB = BC = 1$, угол $\angle B = \frac{5\pi}{6}$, находим сторону $AC$:

$$AC^2 = AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos(\angle B).$$

Подставляем значения:

$$AC^2 = 1^2 + 1^2 — 2 \cdot 1 \cdot 1 \cdot \cos \frac{5\pi}{6} = 1 + 1 — 2 \cdot \left( -\frac{\sqrt{3}}{2} \right).$$ $$AC^2 = 2 + \sqrt{3}.$$

Следовательно:

$$AC = \sqrt{2 + \sqrt{3}}.$$

Используем теорему синусов для нахождения $\sin 15^\circ$:
Теперь применяем теорему синусов:

$$\frac{AB}{\sin \angle C} = \frac{AC}{\sin \angle B}.$$

Подставляем значения:

$$\frac{1}{\sin 15^\circ} = \frac{\sqrt{2 + \sqrt{3}}}{\sin \frac{5\pi}{6}}.$$

Так как $\sin \frac{5\pi}{6} = \frac{1}{2}$, получаем:

$$\sin 15^\circ = \frac{\sin \frac{5\pi}{6}}{\sqrt{2 + \sqrt{3}}} = \frac{\frac{1}{2}}{\sqrt{2 + \sqrt{3}}} = \frac{1}{2\sqrt{2 + \sqrt{3}}}.$$

Чтобы упростить выражение, умножим числитель и знаменатель на $\sqrt{2 — \sqrt{3}}$:

$$\sin 15^\circ = \frac{\sqrt{2}}{2\sqrt{3} + 2\sqrt{3} + 1} = \frac{\sqrt{2}}{2\sqrt{(\sqrt{3} + 1)^2}} = \frac{\sqrt{2}}{2(\sqrt{3} + 1)}.$$

Применяем сопряженное выражение для упрощения:

$$\sin 15^\circ = \frac{\sqrt{2} \cdot (\sqrt{3} — 1)}{2 \cdot (\sqrt{3} + 1)(\sqrt{3} — 1)} = \frac{\sqrt{6} — \sqrt{2}}{2(3 — 1)} = \frac{\sqrt{6} — \sqrt{2}}{4}.$$

Нахождение $\cos 15^\circ$:
Поскольку угол $15^\circ$ лежит в первой четверти, то $\cos 15^\circ$ положительное. Используем тождество:

$$\cos^2 15^\circ = 1 — \sin^2 15^\circ.$$

Подставляем найденное значение $\sin 15^\circ = \frac{\sqrt{6} — \sqrt{2}}{4}$:

$$\cos 15^\circ = \sqrt{1 — \left( \frac{\sqrt{6} — \sqrt{2}}{4} \right)^2}.$$

Вычисляем квадрат синуса:

$$\sin^2 15^\circ = \left( \frac{\sqrt{6} — \sqrt{2}}{4} \right)^2 = \frac{6 — 2\sqrt{12} + 2}{16} = \frac{8 — 4\sqrt{3}}{16} = \frac{2 — \sqrt{3}}{4}.$$

Теперь вычислим $\cos 15^\circ$:

$$\cos 15^\circ = \sqrt{1 — \frac{2 — \sqrt{3}}{4}} = \sqrt{\frac{4 — (2 — \sqrt{3})}{4}} = \sqrt{\frac{2 + \sqrt{3}}{4}} = \frac{\sqrt{2 + \sqrt{3}}}{2}.$$

Ответ для части а):

$$\sin 15^\circ = \frac{\sqrt{6} — \sqrt{2}}{4}; \quad \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}.$$

б) Найти $\sin 22,5^\circ$ и $\cos 22,5^\circ$:

Построим равнобедренный треугольник $\triangle ABC$, у которого:

• $\angle A = \angle C = 22.5^\circ$;
• $AB = BC = 1$.

Этот треугольник также равнобедренный, и его углы $\angle A$ и $\angle C$ равны. Теперь найдем значения $\sin 22,5^\circ$ и $\cos 22,5^\circ$, используя аналогичные методы.

Вычислим угол $\angle B$:

$$\angle B = 180^\circ — \angle A — \angle C = 180^\circ — 22.5^\circ — 22.5^\circ = 135^\circ.$$

Переводим угол в радианы:

$$\angle B = 135^\circ = \frac{\pi \cdot 135^\circ}{180^\circ} = \frac{27\pi}{36} = \frac{3\pi}{4}.$$

Применим теорему косинусов для нахождения стороны $AC$:
По теореме косинусов:

$$AC^2 = AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos \angle B.$$

Подставляем значения:

$$AC^2 = 1^2 + 1^2 — 2 \cdot 1 \cdot 1 \cdot \cos \frac{3\pi}{4} = 1 + 1 — 2 \cdot \left( -\frac{\sqrt{2}}{2} \right) = 2 + \sqrt{2}.$$

Следовательно:

$$AC = \sqrt{2 + \sqrt{2}}.$$

Используем теорему синусов для нахождения $\sin 22,5^\circ$:
Применяем теорему синусов:

$$\frac{AB}{\sin \angle C} = \frac{AC}{\sin \angle B}.$$

Подставляем значения:

$$\frac{1}{\sin 22.5^\circ} = \frac{\sqrt{2 + \sqrt{2}}}{\sin \frac{3\pi}{4}}.$$

Поскольку $\sin \frac{3\pi}{4} = \frac{\sqrt{2}}{2}$, получаем:

$$\sin 22.5^\circ = \frac{\sin \frac{3\pi}{4}}{\sqrt{2 + \sqrt{2}}} = \frac{\frac{\sqrt{2}}{2}}{\sqrt{2 + \sqrt{2}}} = \frac{\sqrt{2}}{2\sqrt{2 + \sqrt{2}}}.$$

Упростим:

$$\sin 22.5^\circ = \frac{\sqrt{2 — \sqrt{2}}}{2}.$$

Нахождение $\cos 22,5^\circ$:
Поскольку угол $22.5^\circ$ лежит в первой четверти, то $\cos 22.5^\circ$ положительное. Используем тождество:

$$\cos^2 22.5^\circ = 1 — \sin^2 22.5^\circ.$$

Подставляем найденное значение $\sin 22.5^\circ$:

$$\cos 22.5^\circ = \sqrt{1 — \left( \frac{\sqrt{2 — \sqrt{2}}}{2} \right)^2} = \sqrt{\frac{4 — (2 — \sqrt{2})}{4}} = \sqrt{\frac{2 + \sqrt{2}}{4}} = \frac{\sqrt{2 + \sqrt{2}}}{2}.$$

Ответ для части б):

$$\sin 22.5^\circ = \frac{\sqrt{2 — \sqrt{2}}}{2}; \quad \cos 22.5^\circ = \frac{\sqrt{2 + \sqrt{2}}}{2}.$$