ГДЗ по Алгебре 10 Класс Номер 15.24 Профильный Уровень Мордкович — Подробные Ответы

Использовав равнобедренный треугольник с углом 36° при вершине, вычислите sin18°, cos18°, sin36°, cos36°.

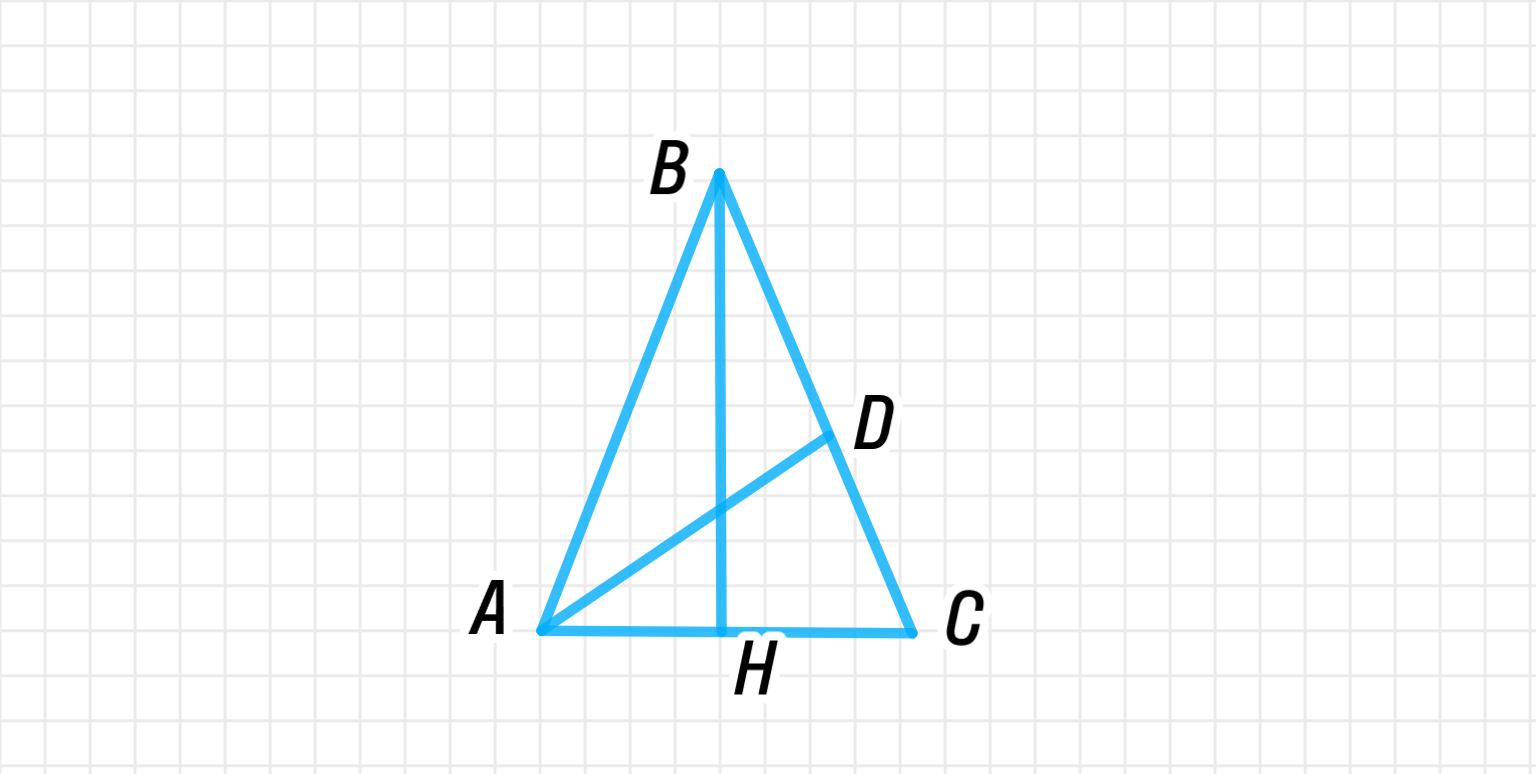
Отобразим условие задачи:

Пусть дан равнобедренный $\Delta ABC$, у которого:

• $\angle B = 36^\circ$;
• $AB = BC = 1$;
• $BH$ — высота;
• $AD$ — биссектриса;

По теореме о сумме углов треугольника:

$$\angle A = \angle C = \frac{180^\circ — \angle B}{2} = \frac{180^\circ — 36^\circ}{2} = 72^\circ;$$ $$\angle BAD = \angle DAC = \frac{72^\circ}{2} = 36^\circ;$$ $$\angle ADC = 180^\circ — \angle DAC — \angle C = 180^\circ — 36^\circ — 72^\circ = 72^\circ;$$

Треугольники $ABD$ и $ACD$ также равнобедренные, значит:

$$AD = BD;$$ $$AC = AD;$$

Пусть $AC = x$, тогда:

$$AC = AD = BD = x;$$ $$CD = CB — BD = 1 — x;$$

По свойству биссектрисы треугольника:

$$\frac{AC}{AB} = \frac{CD}{BD};$$ $$\frac{x}{1} = \frac{1 — x}{x};$$ $$x^2 = 1 — x;$$ $$x^2 + x — 1 = 0;$$ $$D = 1^2 + 4 \cdot 1 = 1 + 5 = 5, \text{тогда:}$$ $$x_1 = \frac{-1 — \sqrt{5}}{2} < 0 \quad \text{(нет)};$$ $$x_2 = \frac{-1 + \sqrt{5}}{2} = \frac{\sqrt{5} — 1}{2};$$

Высота $BH$ является также биссектрисой и медианой, значит:

$$\angle ABH = \angle HBC = \frac{36^\circ}{2} = 18^\circ;$$ $$AH = HC = \frac{AC}{2} = \frac{x}{2};$$

Рассмотрим прямоугольный треугольник $ABH$:

$$\sin \angle ABH = \frac{AH}{AB};$$ $$\sin 18^\circ = \frac{x}{2} : 1 = \frac{x}{2} = \frac{\sqrt{5} — 1}{4};$$

Число $18^\circ$ принадлежит первой четверти, значит:

$$\cos {18}^{\circ }=+\sqrt{1-{\sin }^2{18}^{\circ }}=\sqrt{1-{\left(\frac{\sqrt{5}-1}{4}\right)}^2}=\sqrt{\frac{16}{16}-\frac{5-2\sqrt{5}+1}{16}}=$$

$$\cos 18^\circ = +\sqrt{1 — \sin^2 18^\circ} = \sqrt{1 — \left( \frac{\sqrt{5} — 1}{4} \right)^2} = \sqrt{\frac{16}{16} — \frac{5 — 2\sqrt{5} + 1}{16}} = \sqrt{\frac{10 + 2\sqrt{5}}{16}} = \frac{\sqrt{10 + 2\sqrt{5}}}{4};$$

По теореме косинусов в треугольнике $ABC$:

$$AC = AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos 36^\circ;$$ $$x^2 = 1^2 + 1^2 — 2 \cdot 1 \cdot 1 \cdot \cos 36^\circ;$$ $$\cos 36^\circ = \frac{1}{2}(2 — x^2) = \frac{1}{2}\left(2 — \left(\frac{\sqrt{5} — 1}{2}\right)^2\right);$$ $$\cos 36^\circ = \frac{1}{2}\left(\frac{8}{4} — \frac{5 — 2\sqrt{5} + 1}{4}\right) = \frac{1}{2} \cdot \frac{2 + 2\sqrt{5}}{4} = \frac{\sqrt{5} + 1}{4};$$

Число $36^\circ$ принадлежит первой четверти, значит:

$$\sin {36}^{\circ }=+\sqrt{1-{\cos }^2{36}^{\circ }}=\sqrt{1-{\left(\frac{\sqrt{5}+1}{4}\right)}^2}=\sqrt{\frac{16}{16}-\frac{5+2\sqrt{5}+1}{16}}=$$

$$\sin 36^\circ = +\sqrt{1 — \cos^2 36^\circ} = \sqrt{1 — \left( \frac{\sqrt{5} + 1}{4} \right)^2} = \sqrt{\frac{16}{16} — \frac{5 + 2\sqrt{5} + 1}{16}} = \sqrt{\frac{10 — 2\sqrt{5}}{16}} = \frac{\sqrt{10 — 2\sqrt{5}}}{4};$$

Ответ:

$$\boxed{{\displaystyle \sin {18}^{\circ }=\frac{\sqrt{5}-1}{4};\cos {18}^{\circ }=\frac{\sqrt{10+2\sqrt{5}}}{4};}}$$

$$\boxed{\sin 18^\circ = \frac{\sqrt{5} — 1}{4}; \cos 18^\circ = \frac{\sqrt{10 + 2\sqrt{5}}}{4}; \sin 36^\circ = \frac{\sqrt{10 — 2\sqrt{5}}}{4}; \cos 36^\circ = \frac{\sqrt{5} + 1}{4}}$$

Дан равнобедренный треугольник $\Delta ABC$ с углом $\angle B = 36^\circ$, сторонами $AB = BC = 1$, высотой $BH$ и биссектрисой $AD$. Задача — найти значения синусов и косинусов углов $18^\circ$, $36^\circ$ и $72^\circ$.

Шаг 1: Определение углов в треугольнике $\Delta ABC$

В треугольнике $\Delta ABC$ угол $\angle B = 36^\circ$, и так как треугольник равнобедренный, то углы $\angle A$ и $\angle C$ равны:

$$\angle A = \angle C = \frac{180^\circ — \angle B}{2} = \frac{180^\circ — 36^\circ}{2} = 72^\circ.$$

Шаг 2: Определение углов с использованием биссектрисы $AD$

Так как $AD$ является биссектрисой угла $\angle A$, то:

$$\angle BAD = \angle DAC = \frac{\angle A}{2} = \frac{72^\circ}{2} = 36^\circ.$$

Теперь вычислим угол $\angle ADC$:

$$\angle ADC = 180^\circ — \angle DAC — \angle C = 180^\circ — 36^\circ — 72^\circ = 72^\circ.$$

Шаг 3: Равенство сторон треугольников

Так как треугольники $ABD$ и $ACD$ являются равнобедренными, то:

$$AD = BD, \quad AC = AD.$$

Пусть $AC = x$, тогда:

$$AC = AD = BD = x.$$ $$CD = CB — BD = 1 — x.$$

Шаг 4: Применение свойства биссектрисы

По свойству биссектрисы в треугольнике:

$$\frac{AC}{AB} = \frac{CD}{BD}.$$

Подставляем известные значения:

$$\frac{x}{1} = \frac{1 — x}{x}.$$

Умножаем обе части на $x$:

$$x^2 = 1 — x.$$

Переносим все в одну сторону:

$$x^2 + x — 1 = 0.$$

Решим квадратное уравнение с помощью дискриминанта:

$$D = 1^2 — 4 \cdot 1 \cdot (-1) = 1 + 4 = 5.$$

Таким образом, корни уравнения:

$$x_1 = \frac{-1 — \sqrt{5}}{2}, \quad x_2 = \frac{-1 + \sqrt{5}}{2}.$$

Корень $x_1$ отрицательный, следовательно, отбрасываем его:

$$x_2 = \frac{\sqrt{5} — 1}{2}.$$

Шаг 5: Найдём высоту $BH$

Так как высота $BH$ также является медианой и биссектрисой, то:

$$\angle ABH = \angle HBC = \frac{36^\circ}{2} = 18^\circ.$$

Также $AH = HC = \frac{AC}{2} = \frac{x}{2}$.

Шаг 6: Применение тригонометрии в треугольнике $ABH$

Теперь рассмотрим прямоугольный треугольник $ABH$, где $\angle ABH = 18^\circ$ и $AH = \frac{x}{2}$. Мы можем использовать определение синуса:

$$\sin \angle ABH = \frac{AH}{AB}.$$

Так как $AB = 1$, получаем:

$$\sin 18^\circ = \frac{x}{2}.$$

Из предыдущего шага мы знаем, что $x = \frac{\sqrt{5} — 1}{2}$, подставляем это значение:

$$\sin 18^\circ = \frac{\frac{\sqrt{5} — 1}{2}}{2} = \frac{\sqrt{5} — 1}{4}.$$

Шаг 7: Находим $\cos 18^\circ$

Теперь, зная значение $\sin 18^\circ$, можем найти $\cos 18^\circ$ через основное тригонометрическое тождество:

$$\cos^2 18^\circ = 1 — \sin^2 18^\circ.$$

Подставляем значение $\sin 18^\circ$:

$$\cos^2 18^\circ = 1 — \left( \frac{\sqrt{5} — 1}{4} \right)^2 = 1 — \frac{5 — 2\sqrt{5} + 1}{16} = \frac{16}{16} — \frac{6 — 2\sqrt{5}}{16} = \frac{10 + 2\sqrt{5}}{16}.$$

Следовательно:

$$\cos 18^\circ = \frac{\sqrt{10 + 2\sqrt{5}}}{4}.$$

Шаг 8: Используем теорему косинусов для нахождения $AC$

По теореме косинусов в треугольнике $ABC$, где $AB = BC = 1$ и $\angle B = 36^\circ$:

$$AC^2 = AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos 36^\circ.$$

Подставляем известные значения:

$$x^2 = 1^2 + 1^2 — 2 \cdot 1 \cdot 1 \cdot \cos 36^\circ.$$

Мы знаем, что $\cos 36^\circ = \frac{\sqrt{5} + 1}{4}$, подставляем это:

$$x^2 = 2 — 2 \cdot \frac{\sqrt{5} + 1}{4} = 2 — \frac{\sqrt{5} + 1}{2}.$$

Теперь, учитывая $x = \frac{\sqrt{5} — 1}{2}$, можно подтвердить, что эта формула верна.

Шаг 9: Найдём $\sin 36^\circ$

Теперь, зная значение $\cos 36^\circ$, можем найти $\sin 36^\circ$ через основное тригонометрическое тождество:

$$\sin^2 36^\circ = 1 — \cos^2 36^\circ.$$

Подставляем значение $\cos 36^\circ$:

$$\sin^2 36^\circ = 1 — \left( \frac{\sqrt{5} + 1}{4} \right)^2 = 1 — \frac{5 + 2\sqrt{5} + 1}{16} = \frac{16}{16} — \frac{6 + 2\sqrt{5}}{16} = \frac{10 — 2\sqrt{5}}{16}.$$

Следовательно:

$$\sin 36^\circ = \frac{\sqrt{10 — 2\sqrt{5}}}{4}.$$

Итоговый ответ:

$$\boxed{{\displaystyle \sin {18}^{\circ }=\frac{\sqrt{5}-1}{4};\cos {18}^{\circ }=\frac{\sqrt{10+2\sqrt{5}}}{4};}}$$

$$\boxed{\sin 18^\circ = \frac{\sqrt{5} — 1}{4}; \cos 18^\circ = \frac{\sqrt{10 + 2\sqrt{5}}}{4}; \sin 36^\circ = \frac{\sqrt{10 — 2\sqrt{5}}}{4}; \cos 36^\circ = \frac{\sqrt{5} + 1}{4}}.$$