ГДЗ по Алгебре 10 Класс Номер 16.10 Профильный Уровень Мордкович — Подробные Ответы

а) $y = \sin \left( x — \frac{\pi}{4} \right) + 1$;

б) $y = \sin \left( x + \frac{\pi}{3} \right) — 1$

а) $y = \sin \left( x — \frac{\pi}{4} \right) + 1$;

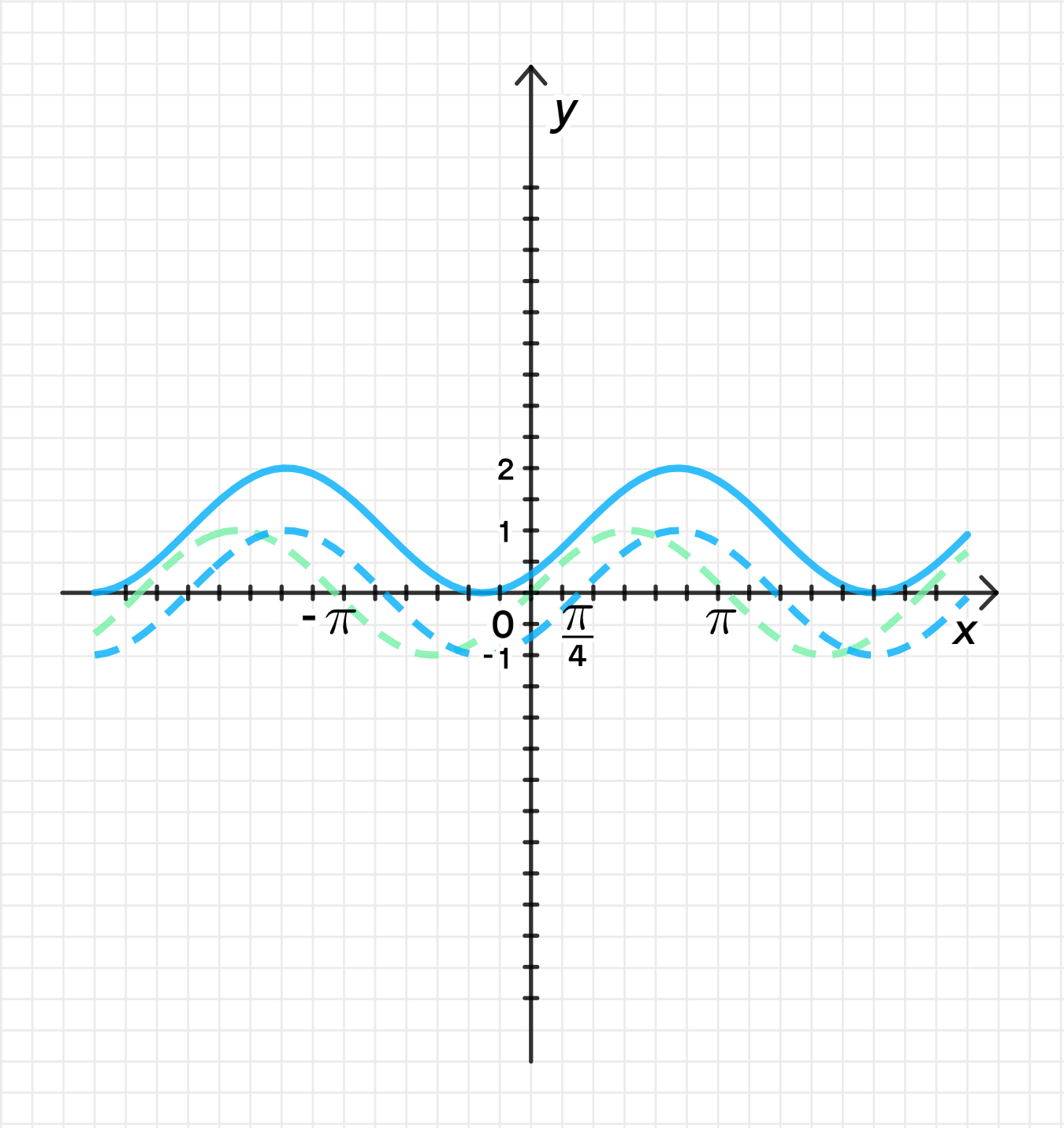
1. Построим график функции $y = \sin x$;
2. Переместим его на $\frac{\pi}{4}$ единицы вправо вдоль оси абсцисс;
3. Переместим новый график на 1 единицу вверх вдоль оси ординат:

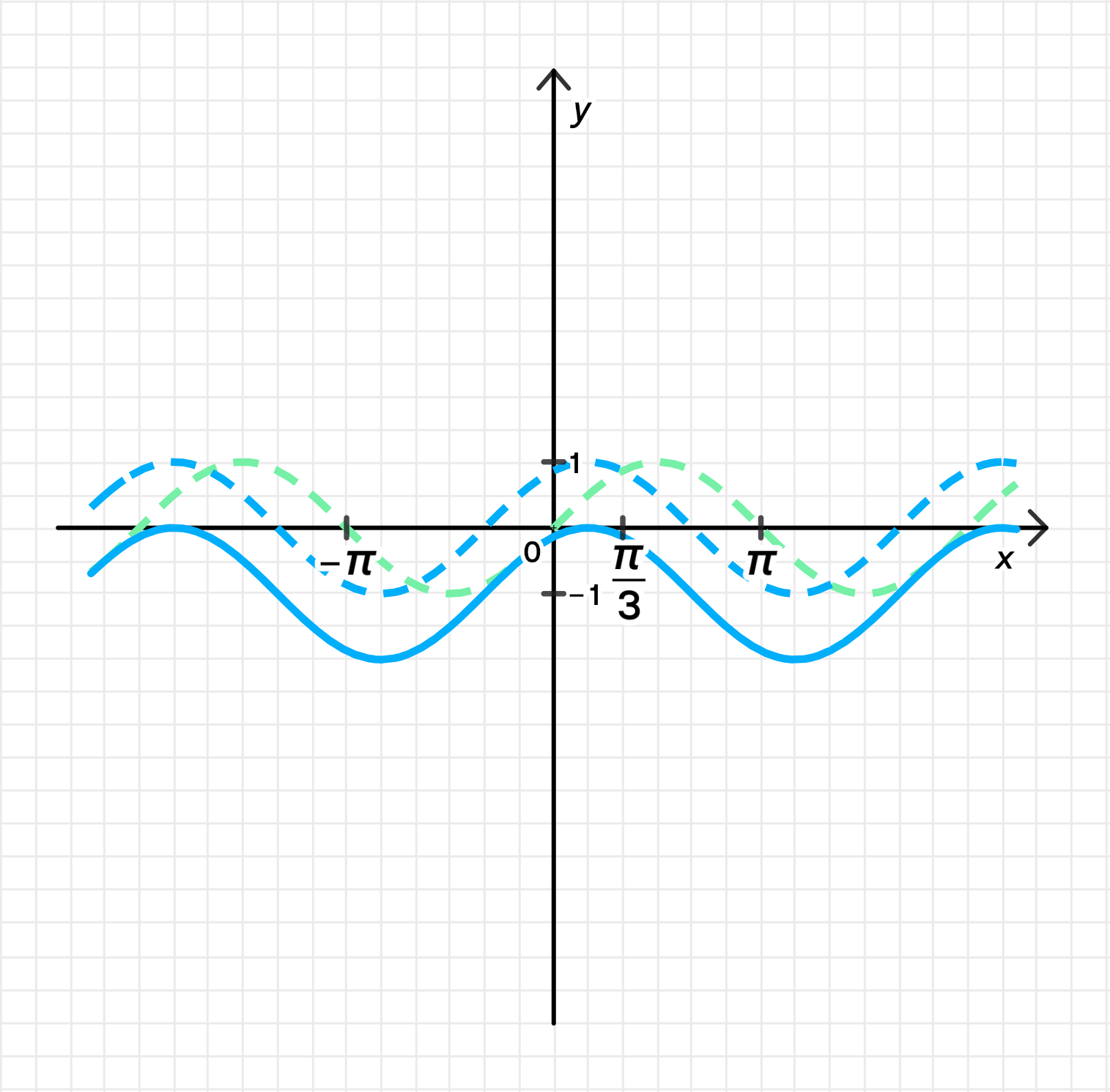
б) $y = \sin \left( x + \frac{\pi}{3} \right) — 1$;

1. Построим график функции $y = \sin x$;
2. Переместим его на $\frac{\pi}{3}$ единицы влево вдоль оси абсцисс;
3. Переместим новый график на 1 единицу вниз вдоль оси ординат:

а) $y = \sin \left( x — \frac{\pi}{4} \right) + 1$

Шаг 1: Построим график функции $y = \sin x$

График функции $y = \sin x$ представляет собой синусоиду с периодом $2\pi$, которая колеблется от $-1$ до $1$. График этой функции проходит через точки:

• $(0, 0)$ — начало цикла,
• $\left( \frac{\pi}{2}, 1 \right)$ — максимум,
• $(\pi, 0)$ — пересечение с осью $x$,
• $\left( \frac{3\pi}{2}, -1 \right)$ — минимум,
• $(2\pi, 0)$ — завершение цикла.

Шаг 2: Переместим график на $\frac{\pi}{4}$ единицы вправо вдоль оси абсцисс

Если в аргументе функции появляется выражение $(x — \frac{\pi}{4})$, это означает сдвиг графика на $\frac{\pi}{4}$ единицы вправо вдоль оси абсцисс. Сдвиг вправо происходит, так как для достижения того же значения функции требуется увеличить $x$ на $\frac{\pi}{4}$. Таким образом, график будет начинаться с точки $\left( \frac{\pi}{4}, 0 \right)$, а его форма будет оставаться прежней, просто он будет сдвигаться вправо.

Шаг 3: Переместим новый график на 1 единицу вверх вдоль оси ординат

Если к функции добавляется постоянное значение $+1$, это означает сдвиг графика на 1 единицу вверх вдоль оси ординат. Теперь вся синусоида будет находиться на уровне $y = 1$, и точки, которые раньше были на оси $x$, будут перемещены на 1 единицу вверх.

Результат:

График функции $y = \sin \left( x — \frac{\pi}{4} \right) + 1$ сдвигается на $\frac{\pi}{4}$ единицы вправо и на 1 единицу вверх.

б) $y = \sin \left( x + \frac{\pi}{3} \right) — 1$

Шаг 1: Построим график функции $y = \sin x$

Как и в предыдущем случае, график функции $y = \sin x$ представляет собой синусоиду с периодом $2\pi$, колеблющуюся от $-1$ до $1$.

Шаг 2: Переместим график на $\frac{\pi}{3}$ единицы влево вдоль оси абсцисс

Если в аргументе функции появляется выражение $(x + \frac{\pi}{3})$, это означает сдвиг графика на $\frac{\pi}{3}$ единицы влево вдоль оси абсцисс. Это происходит, потому что для достижения того же значения функции теперь требуется уменьшить значение $x$ на $\frac{\pi}{3}$. Таким образом, график будет начинаться с точки $\left( -\frac{\pi}{3}, 0 \right)$, а его форма останется неизменной, просто сдвинется влево.

Шаг 3: Переместим новый график на 1 единицу вниз вдоль оси ординат

Если от функции отнимается постоянное значение $-1$, это означает сдвиг графика на 1 единицу вниз вдоль оси ординат. Теперь вся синусоида будет находиться на уровне $y = -1$, и точки, которые раньше располагались на оси $x$, будут перемещены на 1 единицу вниз.

Результат:

График функции $y = \sin \left( x + \frac{\pi}{3} \right) — 1$ сдвигается на $\frac{\pi}{3}$ единицы влево и на 1 единицу вниз.