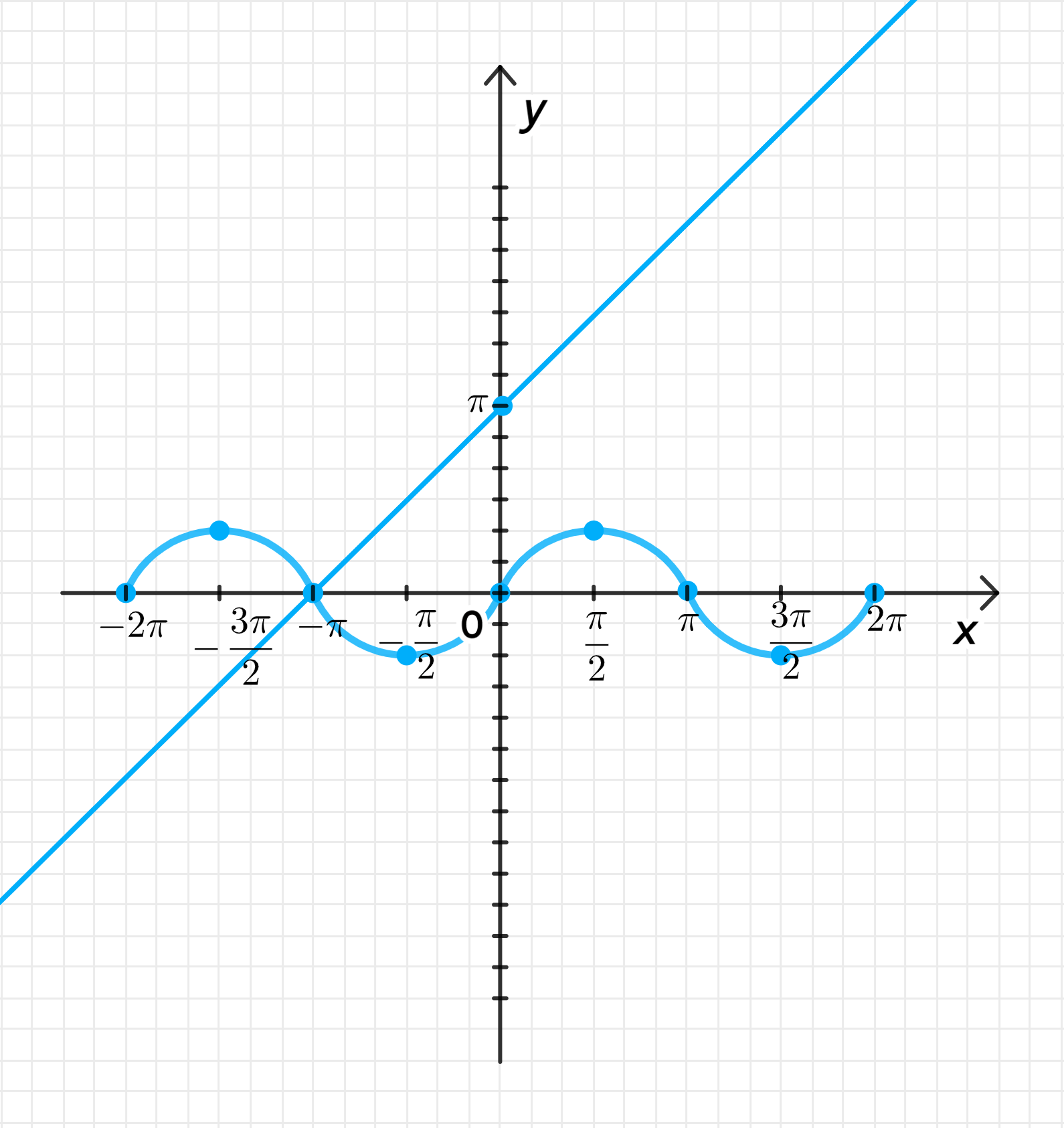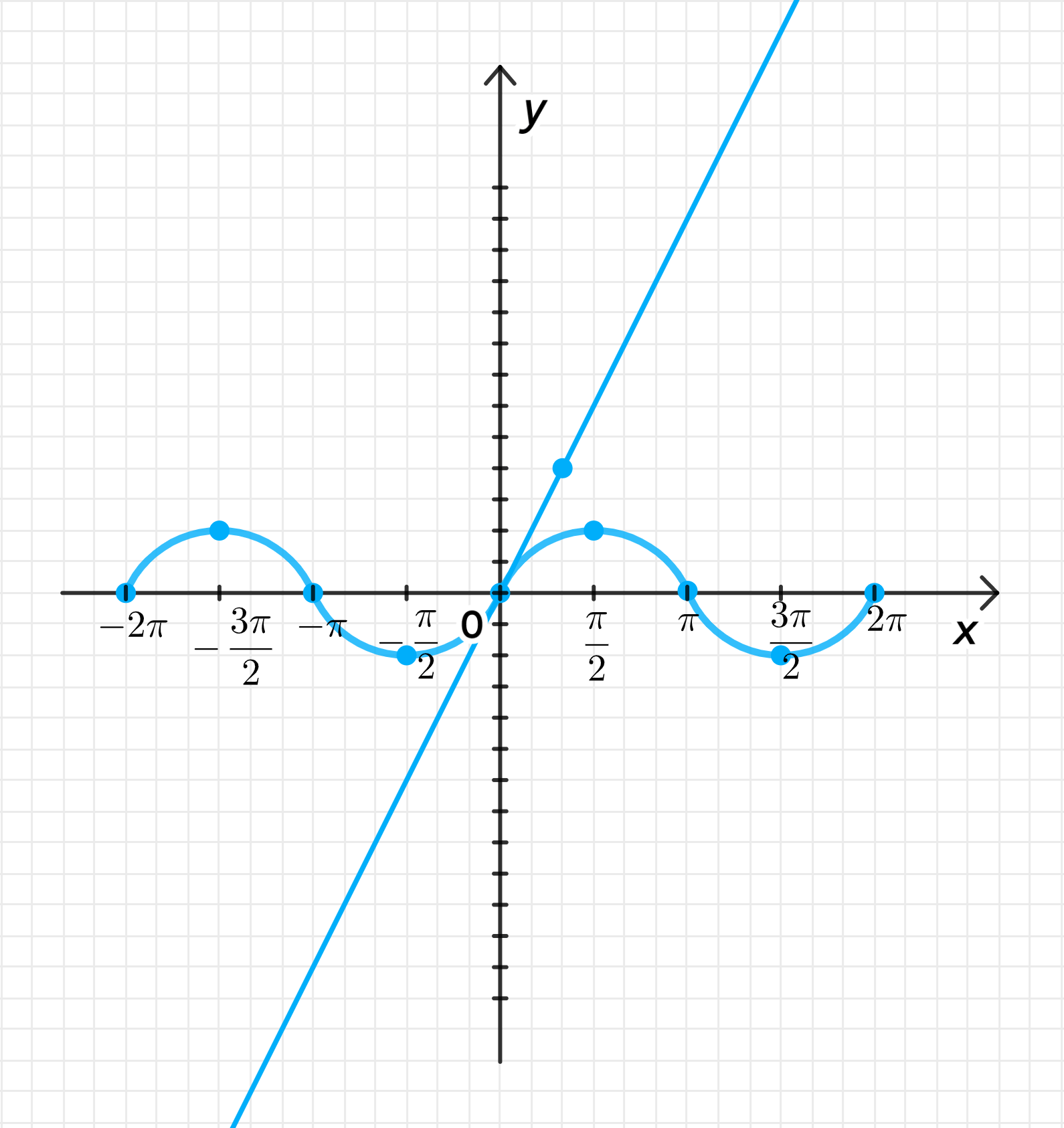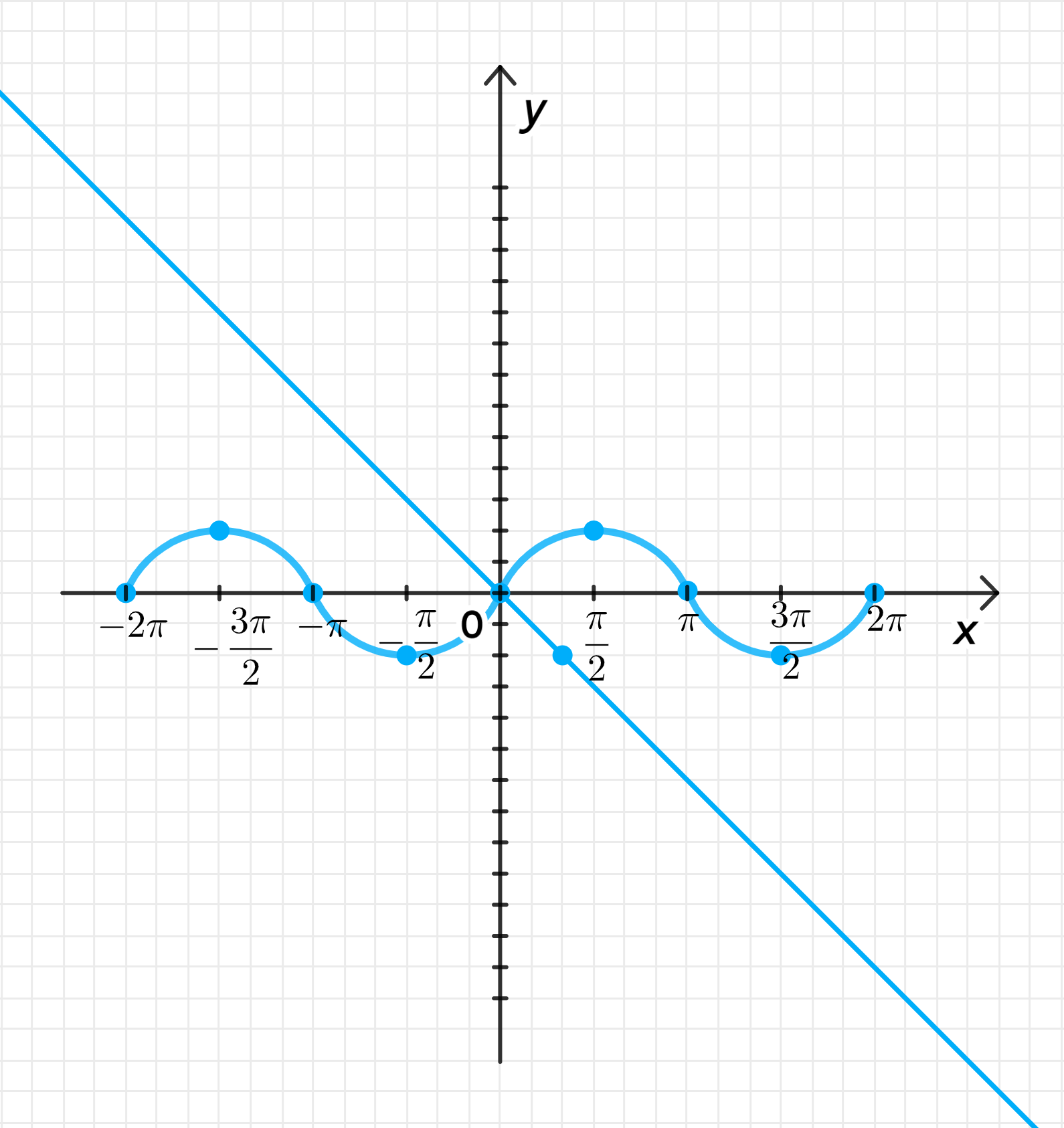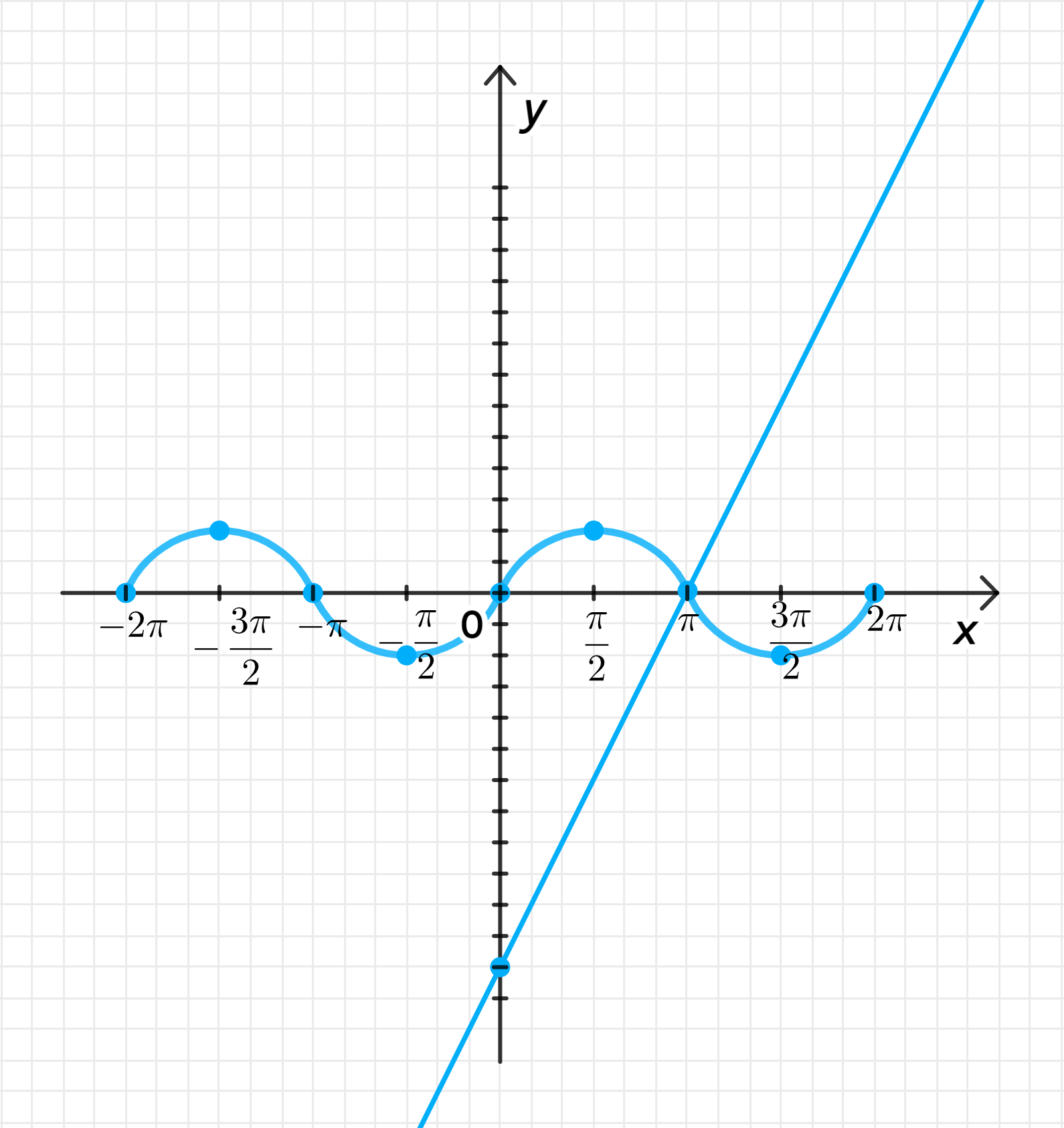ГДЗ по Алгебре 10 Класс Номер 16.19 Профильный Уровень Мордкович — Подробные Ответы

Решите графически уравнение:

а) $\sin x = x + \pi$

б) $\sin x = 2x$

в) $\sin x + x = 0$

г) $\sin x=2x-2\pi$

а) $\sin x = x + \pi$

$y = \sin x$ — уравнение синусоиды;

$y = x + \pi$ — уравнение прямой:

Графики функций:

Ответ: $x = -\pi$.

б) $\sin x = 2x$

$y = \sin x$ — уравнение синусоиды;

$y = 2x$ — уравнение прямой:

Графики функций:

Ответ: $x = 0$.

в) $\sin x + x = 0$

Преобразуем уравнение:

$$\sin x = -x;$$

$y = \sin x$ — уравнение синусоиды;

$y = -x$ — уравнение прямой:

Графики функций:

Ответ: $x = 0$.

г) $\sin x = 2x — 2\pi$

$y = \sin x$ — уравнение синусоиды;

$y = 2x — 2\pi$ — уравнение прямой:

Графики функций:

Ответ: $x = \pi$.

а) $\sin x = x + \pi$

1. Уравнение синусоиды и прямой:

Для начала рассмотрим обе функции:

• $y = \sin x$ — уравнение синусоиды, график которой представляет собой волну, колеблющуюся от $-1$ до $1$, с периодом $2\pi$.
• $y = x + \pi$ — уравнение прямой. Это линейная функция, которая при $x = 0$ имеет значение $y = \pi$ и с каждым увеличением $x$ значение $y$ увеличивается на единицу.

2. Вычисление значений для построения графиков:

Для более наглядного представления мы подставим несколько значений $x$ в обе функции, чтобы понять, как ведут себя графики:

• Для $y = \sin x$:
  • При $x = -\pi$, $y = \sin(-\pi) = 0$.
  • При $x = 0$, $y = \sin(0) = 0$.
• Для $y = x + \pi$:
  • При $x = -\pi$, $y = -\pi + \pi = 0$.
  • При $x = 0$, $y = 0 + \pi = \pi \approx 3.1416$.

3. Построение графиков функций:

• График $y = \sin x$ будет волнообразным, начиная с нулевой точки, с колебаниями.
• График $y = x + \pi$ будет прямой, пересекающей ось $y = 0$ в точке $x = -\pi$.

4. Пересечение графиков:

Для нахождения точек пересечения этих графиков необходимо решить уравнение:

$$\sin x = x + \pi$$

Для этого можно использовать численные методы (например, метод Ньютона) или графически. Очевидно, что один из корней находится в точке $x = -\pi$, поскольку в этой точке обе функции равны нулю. На графике видно, что это точка пересечения.

Ответ: $x = -\pi$.

б) $\sin x = 2x$

1. Уравнение синусоиды и прямой:

• $y = \sin x$ — уравнение синусоиды.
• $y = 2x$ — уравнение прямой, которая проходит через начало координат с угловым коэффициентом $2$.

2. Вычисление значений для построения графиков:

• Для $y = \sin x$:
  • При $x = 0$, $y = \sin(0) = 0$.
  • При $x = 1$, $y = \sin(1) \approx 0.841$.
• Для $y = 2x$:
  • При $x = 0$, $y = 2(0) = 0$.
  • При $x = 1$, $y = 2(1) = 2$.

3. Построение графиков функций:

• График $y = \sin x$ — волнообразная функция, колеблющаяся от $-1$ до $1$.
• График $y = 2x$ — прямая, растущая с угловым коэффициентом 2.

4. Пересечение графиков:

Решаем уравнение:

$$\sin x = 2x$$

Очевидно, что для $x = 0$ обе функции равны нулю. Для нахождения других решений нужно использовать численные методы, но из графика видно, что кроме $x = 0$ другие пересечения не наблюдаются.

Ответ: $x = 0$.

в) $\sin x + x = 0$

1. Преобразование уравнения:

Для удобства перепишем уравнение:

$$\sin x = -x$$

2. Уравнение синусоиды и прямой:

• $y = \sin x$ — уравнение синусоиды.
• $y = -x$ — уравнение прямой, которая проходит через начало координат и имеет угловой коэффициент $-1$.

3. Вычисление значений для построения графиков:

• Для $y = \sin x$:
  • При $x = 0$, $y = \sin(0) = 0$.
  • При $x = 1$, $y = \sin(1) \approx 0.841$.
• Для $y = -x$:
  • При $x = 0$, $y = -0 = 0$.
  • При $x = 1$, $y = -1$.

4. Построение графиков функций:

• График $y = \sin x$ будет волнообразным, колеблющимся от $-1$ до $1$.
• График $y = -x$ — прямая с угловым коэффициентом $-1$.

5. Пересечение графиков:

Решаем уравнение:

$$\sin x = -x$$

Очевидно, что для $x = 0$ обе функции равны нулю. По графику видно, что больше пересечений не происходит.

Ответ: $x = 0$.

г) $\sin x = 2x — 2\pi$

1. Уравнение синусоиды и прямой:

• $y = \sin x$ — уравнение синусоиды.
• $y = 2x — 2\pi$ — уравнение прямой с угловым коэффициентом $2$, но с сдвигом по оси $y$ на $-2\pi$.

2. Вычисление значений для построения графиков:

• Для $y = \sin x$:
  • При $x = 0$, $y = \sin(0) = 0$.
  • При $x = \pi$, $y = \sin(\pi) = 0$.
• Для $y = 2x — 2\pi$:
  • При $x = \frac{5\pi}{6}$, $y = 2 \cdot \frac{5\pi}{6} — 2\pi = -1$.
  • При $x = \pi$, $y = 2\pi — 2\pi = 0$.

3. Построение графиков функций:

• График $y = \sin x$ будет волнообразным, колеблющимся от $-1$ до $1$.
• График $y = 2x — 2\pi$ будет прямой с угловым коэффициентом 2, сдвинутой на $-2\pi$ по оси $y$.

4. Пересечение графиков:

Решаем уравнение:

$$\sin x = 2x — 2\pi$$

Очевидно, что для $x = \pi$ обе функции равны нулю. На графике видно, что точка пересечения находится в точке $x = \pi$.

Ответ: $x = \pi$.

Итоговые ответы:

• а) $x = -\pi$
• б) $x = 0$
• в) $x = 0$
• г) $x = \pi$