ГДЗ по Алгебре 10 Класс Номер 16.40 Профильный Уровень Мордкович — Подробные Ответы

а) $y = \cos\left(x + \frac{\pi}{2}\right) + 1$;

б) $y = \cos\left(x — \frac{\pi}{3}\right) — 2$;

в) $y = \cos\left(x — \frac{\pi}{2}\right) + \frac{1}{2}$;

г) $y = \cos\left(x + \frac{\pi}{6}\right) — 3$

а) $y = \cos\left(x + \frac{\pi}{2}\right) + 1$;

Построим график функции $y = \cos x$;

Переместим его на $\frac{\pi}{2}$ единицы влево вдоль оси абсцисс;

Переместим новый график на 1 единицу вверх вдоль оси ординат:

б) $y = \cos\left(x — \frac{\pi}{3}\right) — 2$;

Построим график функции $y = \cos x$;

Переместим его на $\frac{\pi}{3}$ единицы вправо вдоль оси абсцисс;

Переместим новый график на 2 единицы вниз вдоль оси ординат:

в) $y = \cos\left(x — \frac{\pi}{2}\right) + \frac{1}{2}$;

Построим график функции $y = \cos x$;

Переместим его на $\frac{\pi}{2}$ единицы вправо вдоль оси абсцисс;

Переместим новый график на $\frac{1}{2}$ единицы вверх вдоль оси ординат:

г) $y = \cos\left(x + \frac{\pi}{6}\right) — 3$;

Построим график функции $y = \cos x$;

Переместим его на $\frac{\pi}{6}$ единицы влево вдоль оси абсцисс;

Переместим новый график на 3 единицы вниз вдоль оси ординат:

а) $y = \cos\left(x + \frac{\pi}{2}\right) + 1$

1. Построение графика функции $y = \cos x$:

• График функции $y = \cos x$ представляет собой периодическую волну, которая колеблется между -1 и 1 по оси $y$, с периодом $2\pi$ и амплитудой 1.
• Этот график начинается в точке $(0, 1)$, проходит через точку $\left( \frac{\pi}{2}, 0 \right)$, достигает минимума в $(\pi, -1)$, и затем снова возвращается к 1 в точке $(2\pi, 1)$.

2. Перемещение графика на $\frac{\pi}{2}$ единицы влево вдоль оси абсцисс:

• В аргументе функции $\cos\left(x + \frac{\pi}{2}\right)$ присутствует слагаемое $+\frac{\pi}{2}$, что указывает на сдвиг графика влево на $\frac{\pi}{2}$ единицы.
• Это означает, что каждая точка на графике функции $y = \cos x$ будет перемещена влево на $\frac{\pi}{2}$. Например:
  • Точка, где $\cos x = 1$ для $x = 0$, будет перемещена в точку $x = -\frac{\pi}{2}$.
  • Точка, где $\cos x = 0$ для $x = \frac{\pi}{2}$, будет перемещена в точку $x = 0$.
  • Точка, где $\cos x = -1$ для $x = \pi$, будет перемещена в точку $x = \frac{\pi}{2}$.

3. Перемещение нового графика на 1 единицу вверх вдоль оси ординат:

• После того как мы сдвинули график влево на $\frac{\pi}{2}$, теперь нужно переместить его на 1 единицу вверх вдоль оси $y$.
• Это означает, что каждая точка на графике будет увеличена на 1 по оси $y$. Например:
  • Точка $\left( -\frac{\pi}{2}, 1 \right)$ станет $\left( -\frac{\pi}{2}, 2 \right)$.
  • Точка $(0, 0)$ станет $(0, 1)$.
  • Точка $\left( \frac{\pi}{2}, -1 \right)$ станет $\left( \frac{\pi}{2}, 0 \right)$.
• Результат — это сдвинутый график функции $y = \cos x$, который теперь будет колебаться между 0 и 2, и сдвигаться влево на $\frac{\pi}{2}$.

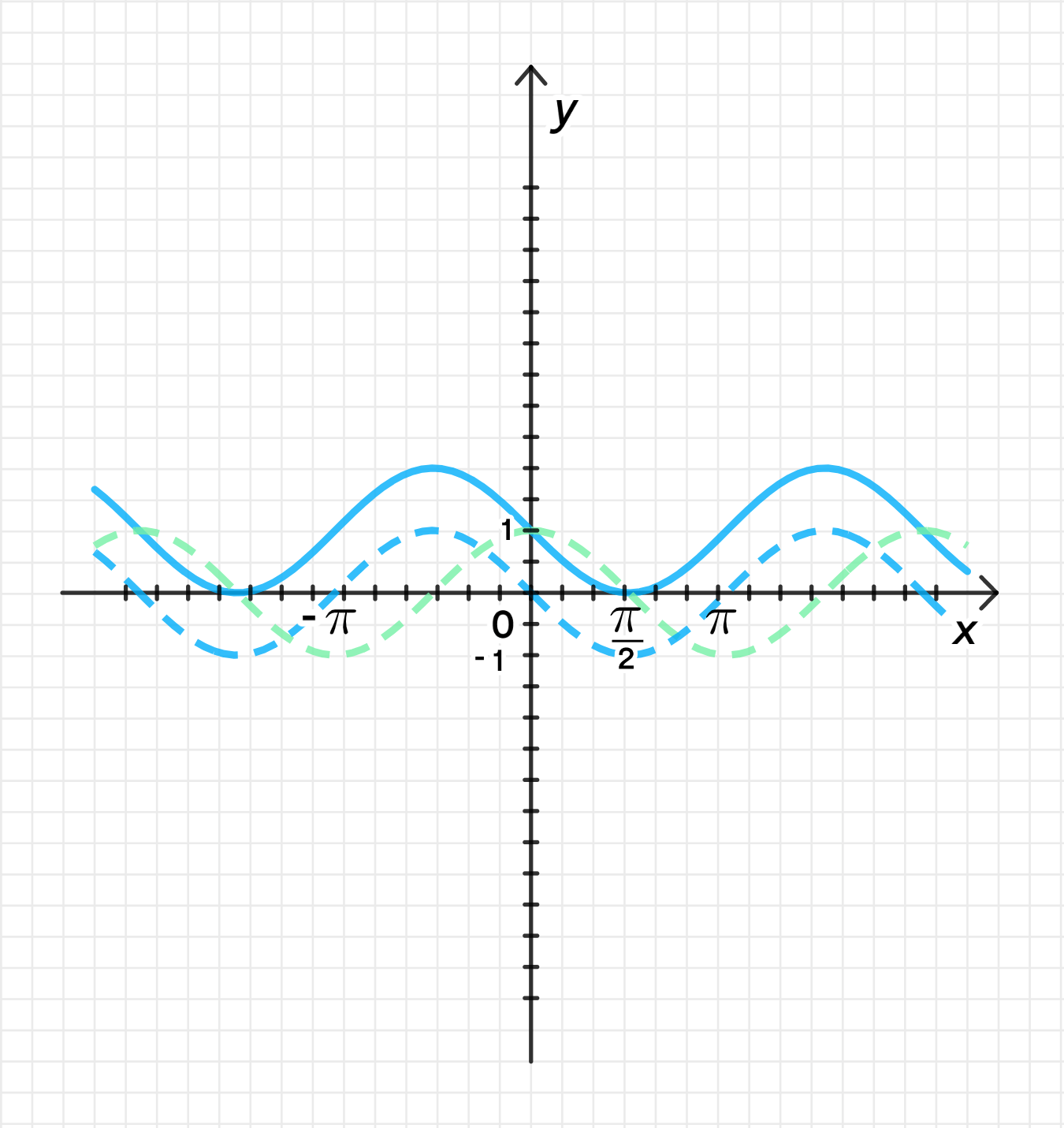
График для а):

б) $y = \cos\left(x — \frac{\pi}{3}\right) — 2$

1. Построение графика функции $y = \cos x$:

• Строим график функции $y = \cos x$, как описано в первом пункте.

2. Перемещение графика на $\frac{\pi}{3}$ единицы вправо вдоль оси абсцисс:

• В аргументе функции $\cos\left(x — \frac{\pi}{3}\right)$ присутствует слагаемое $-\frac{\pi}{3}$, что указывает на сдвиг графика вправо на $\frac{\pi}{3}$ единицы.
• Это означает, что каждая точка на графике функции $y = \cos x$ будет перемещена вправо на $\frac{\pi}{3}$.
  • Точка, где $\cos x = 1$ для $x = 0$, теперь будет находиться в точке $x = \frac{\pi}{3}$.
  • Точка, где $\cos x = 0$ для $x = \frac{\pi}{2}$, теперь будет находиться в точке $x = \frac{\pi}{2} + \frac{\pi}{3} = \frac{5\pi}{6}$.
  • Точка, где $\cos x = -1$ для $x = \pi$, теперь будет находиться в точке $x = \pi + \frac{\pi}{3} = \frac{4\pi}{3}$.

3. Перемещение нового графика на 2 единицы вниз вдоль оси ординат:

• После того как график был сдвинут вправо на $\frac{\pi}{3}$, теперь нужно переместить его вниз на 2 единицы вдоль оси $y$.
• Это означает, что каждая точка на графике будет уменьшена на 2.
  • Точка $\left( \frac{\pi}{3}, 1 \right)$ станет $\left( \frac{\pi}{3}, -1 \right)$.
  • Точка $\left( \frac{5\pi}{6}, 0 \right)$ станет $\left( \frac{5\pi}{6}, -2 \right)$.
  • Точка $\left( \frac{4\pi}{3}, -1 \right)$ станет $\left( \frac{4\pi}{3}, -3 \right)$.

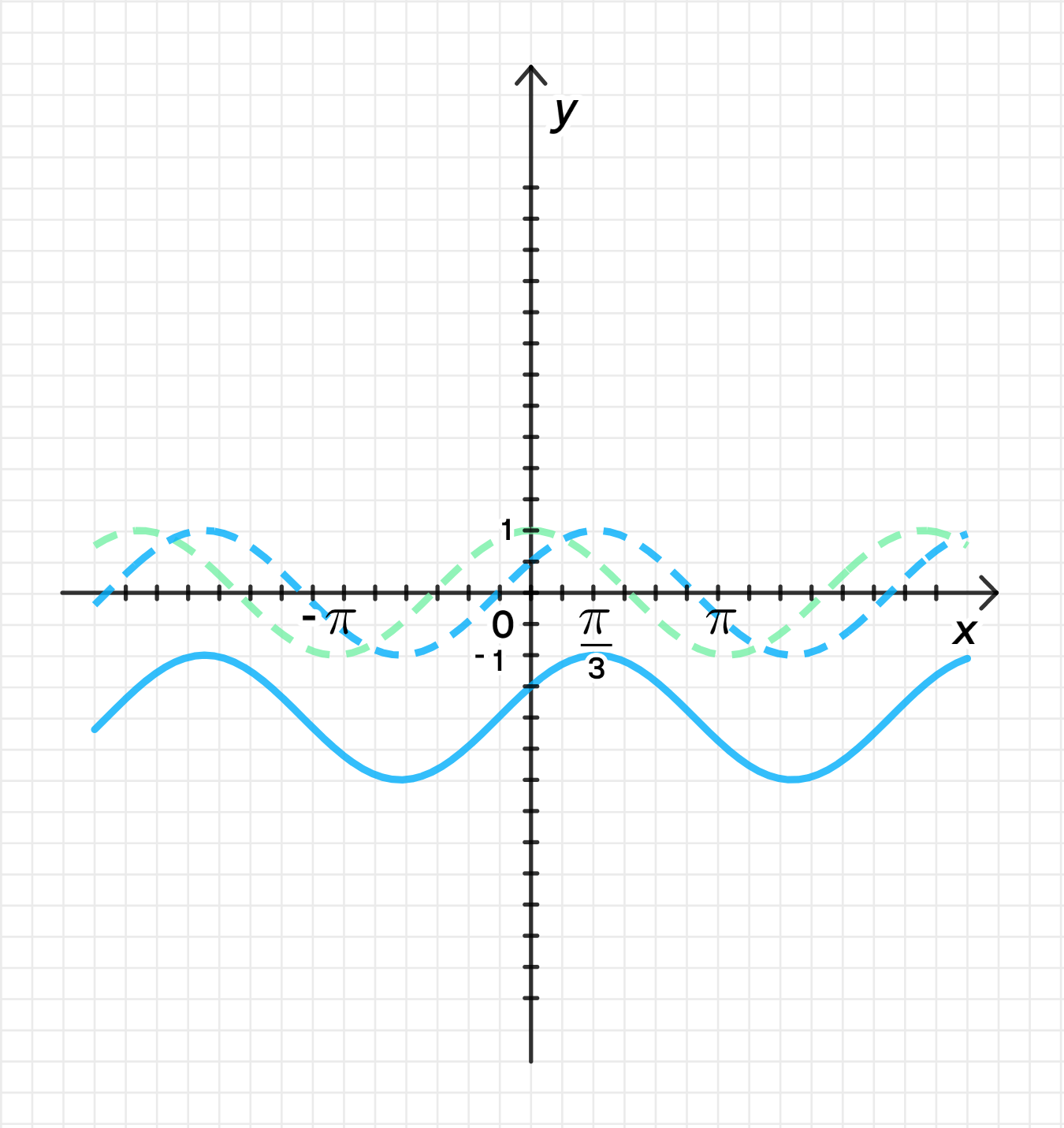
График для б):

в) $y = \cos\left(x — \frac{\pi}{2}\right) + \frac{1}{2}$

1. Построение графика функции $y = \cos x$:

• Строим график стандартной функции $y = \cos x$, как описано выше.

2. Перемещение графика на $\frac{\pi}{2}$ единицы вправо вдоль оси абсцисс:

• В аргументе функции $\cos\left(x — \frac{\pi}{2}\right)$ присутствует слагаемое $-\frac{\pi}{2}$, что указывает на сдвиг графика вправо на $\frac{\pi}{2}$ единицы.
• Это означает, что каждая точка на графике будет перемещена вправо на $\frac{\pi}{2}$. Например:
  • Точка $\cos x = 1$ для $x = 0$ будет сдвинута в точку $x = \frac{\pi}{2}$.
  • Точка $\cos x = 0$ для $x = \frac{\pi}{2}$ будет сдвинута в точку $x = \pi$.
  • Точка $\cos x = -1$ для $x = \pi$ будет сдвинута в точку $x = \frac{3\pi}{2}$.

3. Перемещение нового графика на $\frac{1}{2}$ единицы вверх вдоль оси ординат:

• После сдвига вправо на $\frac{\pi}{2}$ единиц, теперь нужно переместить график на $\frac{1}{2}$ единицы вверх.
• Каждая точка на графике будет увеличена на $\frac{1}{2}$:
  • Точка $\left( \frac{\pi}{2}, 1 \right)$ станет $\left( \frac{\pi}{2}, 1.5 \right)$.
  • Точка $(\pi, 0)$ станет $(\pi, 0.5)$.
  • Точка $\left( \frac{3\pi}{2}, -1 \right)$ станет $\left( \frac{3\pi}{2}, -0.5 \right)$.

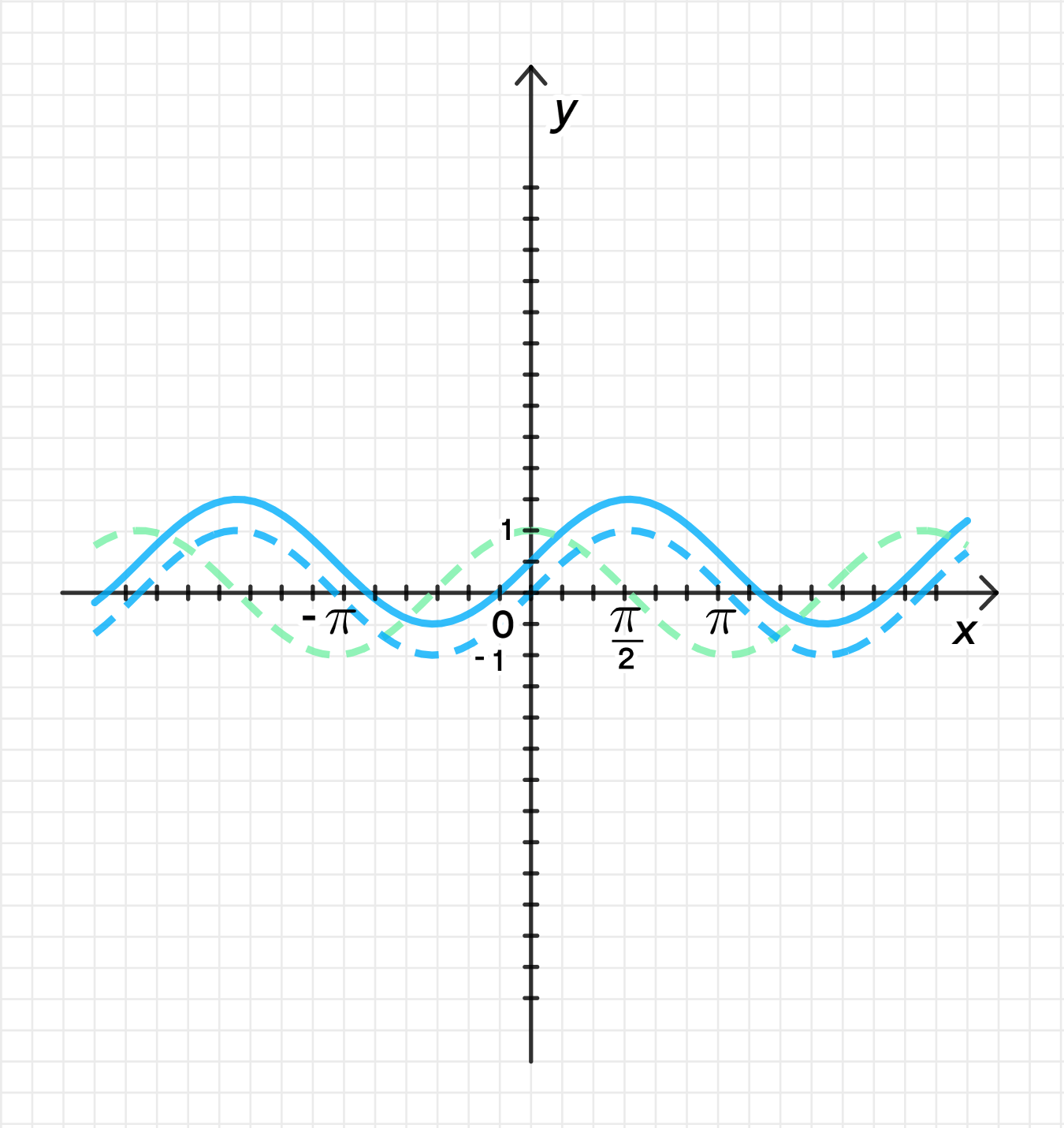
График для в):

г) $y = \cos\left(x + \frac{\pi}{6}\right) — 3$

1. Построение графика функции $y = \cos x$:

• Строим стандартный график функции $y = \cos x$.

2. Перемещение графика на $\frac{\pi}{6}$ единицы влево вдоль оси абсцисс:

• В аргументе функции $\cos\left(x + \frac{\pi}{6}\right)$ присутствует слагаемое $+\frac{\pi}{6}$, что указывает на сдвиг графика влево на $\frac{\pi}{6}$ единицы.
• Это означает, что каждая точка на графике будет сдвинута влево на $\frac{\pi}{6}$. Например:
  • Точка $\cos x = 1$ для $x = 0$ будет сдвинута в точку $x = -\frac{\pi}{6}$.
  • Точка $\cos x = 0$ для $x = \frac{\pi}{2}$ будет сдвинута в точку $x = \frac{\pi}{2} — \frac{\pi}{6} = \frac{\pi}{3}$.
  • Точка $\cos x = -1$ для $x = \pi$ будет сдвинута в точку $x = \pi — \frac{\pi}{6} = \frac{5\pi}{6}$.

3. Перемещение нового графика на 3 единицы вниз вдоль оси ординат:

• После сдвига влево на $\frac{\pi}{6}$, график сдвигается вниз на 3 единицы.
• Это означает, что каждая точка на графике будет уменьшена на 3:
  • Точка $\left( -\frac{\pi}{6}, 1 \right)$ станет $\left( -\frac{\pi}{6}, -2 \right)$.
  • Точка $\left( \frac{\pi}{3}, 0 \right)$ станет $\left( \frac{\pi}{3}, -3 \right)$.
  • Точка $\left( \frac{5\pi}{6}, -1 \right)$ станет $\left( \frac{5\pi}{6}, -4 \right)$.

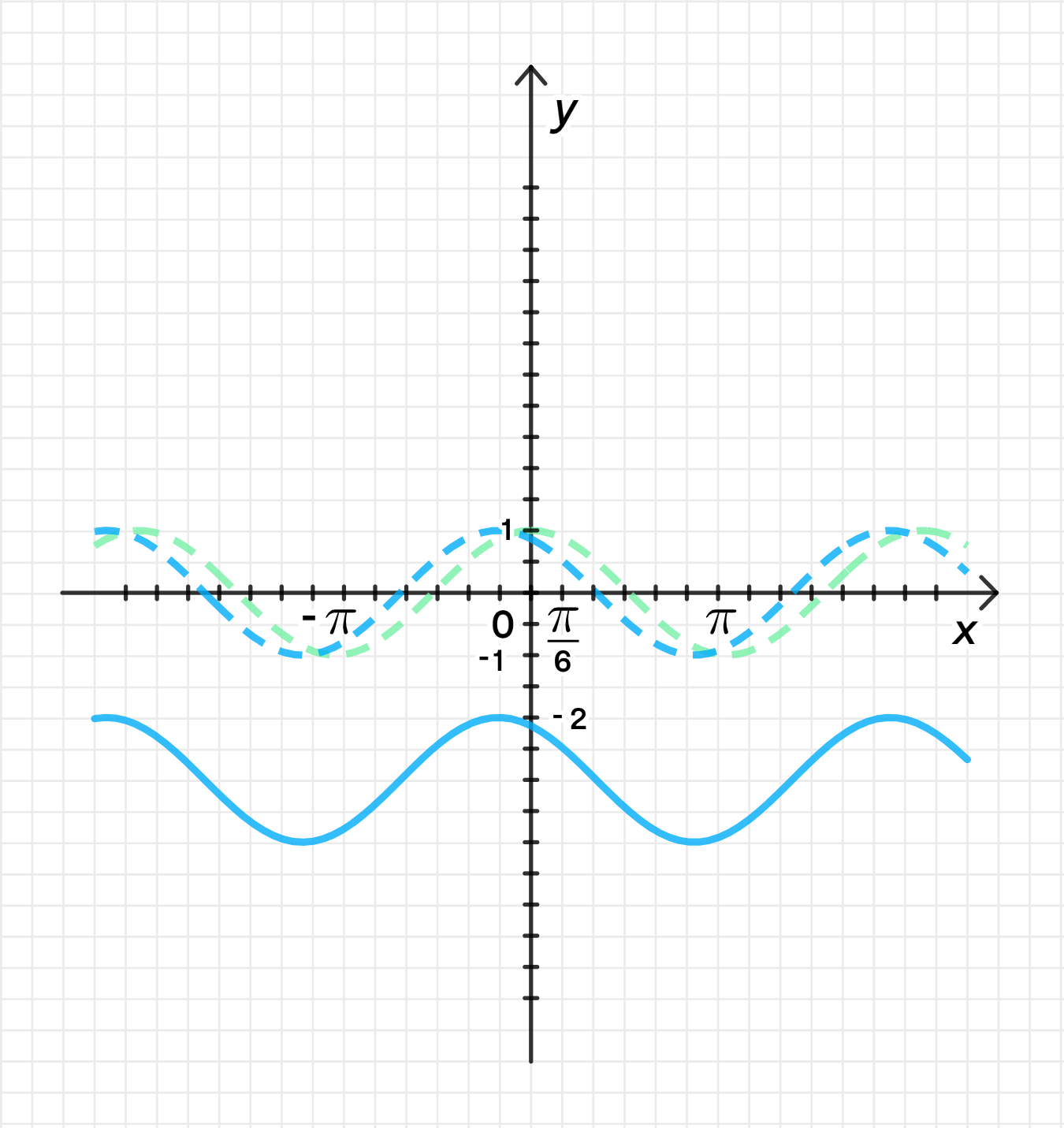
График для г):