ГДЗ по Алгебре 10 Класс Номер 16.47 Профильный Уровень Мордкович — Подробные Ответы

Решите графически уравнение:

а) $\cos x = x + \frac{\pi}{2}$;

б) $-\cos x = 3x — 1$;

в) $\cos x = 2x + 1$;

г) $\cos x = -x + \frac{\pi}{2}$

а) $\cos x = x + \frac{\pi}{2}$;

$y = \cos x$ — уравнение синусоиды;

$y = x + \frac{\pi}{2}$ — уравнение прямой:

Графики функций:

Ответ: $x = -\frac{\pi}{2}$.

б) $-\cos x = 3x — 1$;

Преобразуем выражение:

$$\cos x = 1 — 3x;$$

$y = \cos x$ — уравнение синусоиды;

$y = 1 — 3x$ — уравнение прямой:

Графики функций:

Ответ: $x = 0$.

в) $\cos x = 2x + 1$;

$y = \cos x$ — уравнение синусоиды;

$y = 2x + 1$ — уравнение прямой:

Графики функций:

Ответ: $x = 0$.

г) $\cos x = -x + \frac{\pi}{2}$;

$y = \cos x$ — уравнение синусоиды;

$y = -x + \frac{\pi}{2}$ — уравнение прямой:

Графики функций:

Ответ: $x = \frac{\pi}{2}$.

а) $\cos x = x + \frac{\pi}{2}$

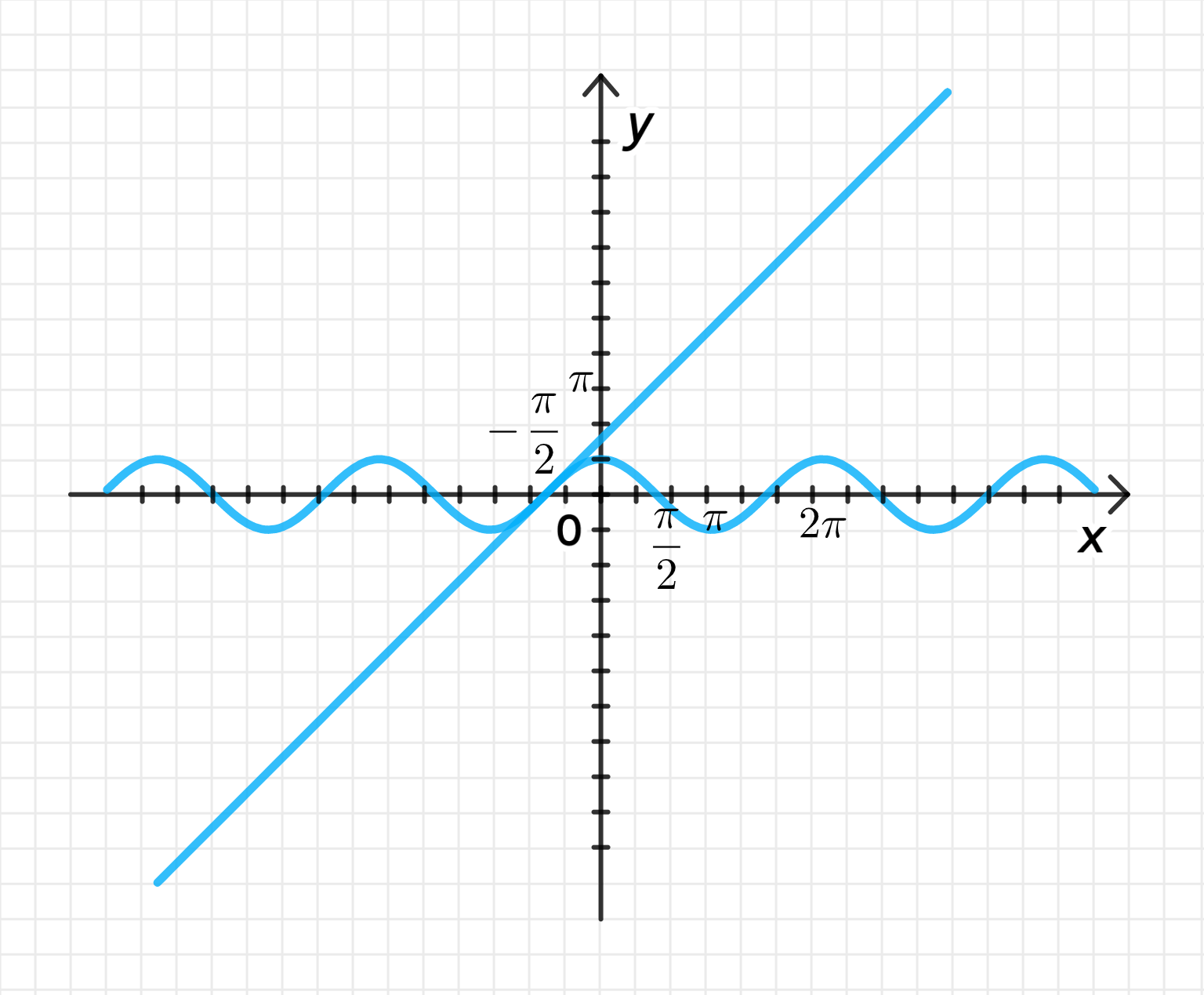
Анализ функции:

• Функция $y = \cos x$ — это уравнение синусоиды, которая колеблется между -1 и 1 с периодом $2\pi$.
• Функция $y = x + \frac{\pi}{2}$ — это уравнение прямой с угловым коэффициентом 1 и сдвигом по оси $y$ на $\frac{\pi}{2}$.

Построение таблицы значений:
Чтобы понимать, где эти функции могут пересекаться, посчитаем значения обеих функций для нескольких значений $x$:

Мы видим, что при $x = -\frac{\pi}{2}$, обе функции равны нулю, то есть это точка пересечения.

Графики функций:

Ответ:
Пересечение происходит при $x = -\frac{\pi}{2}$.

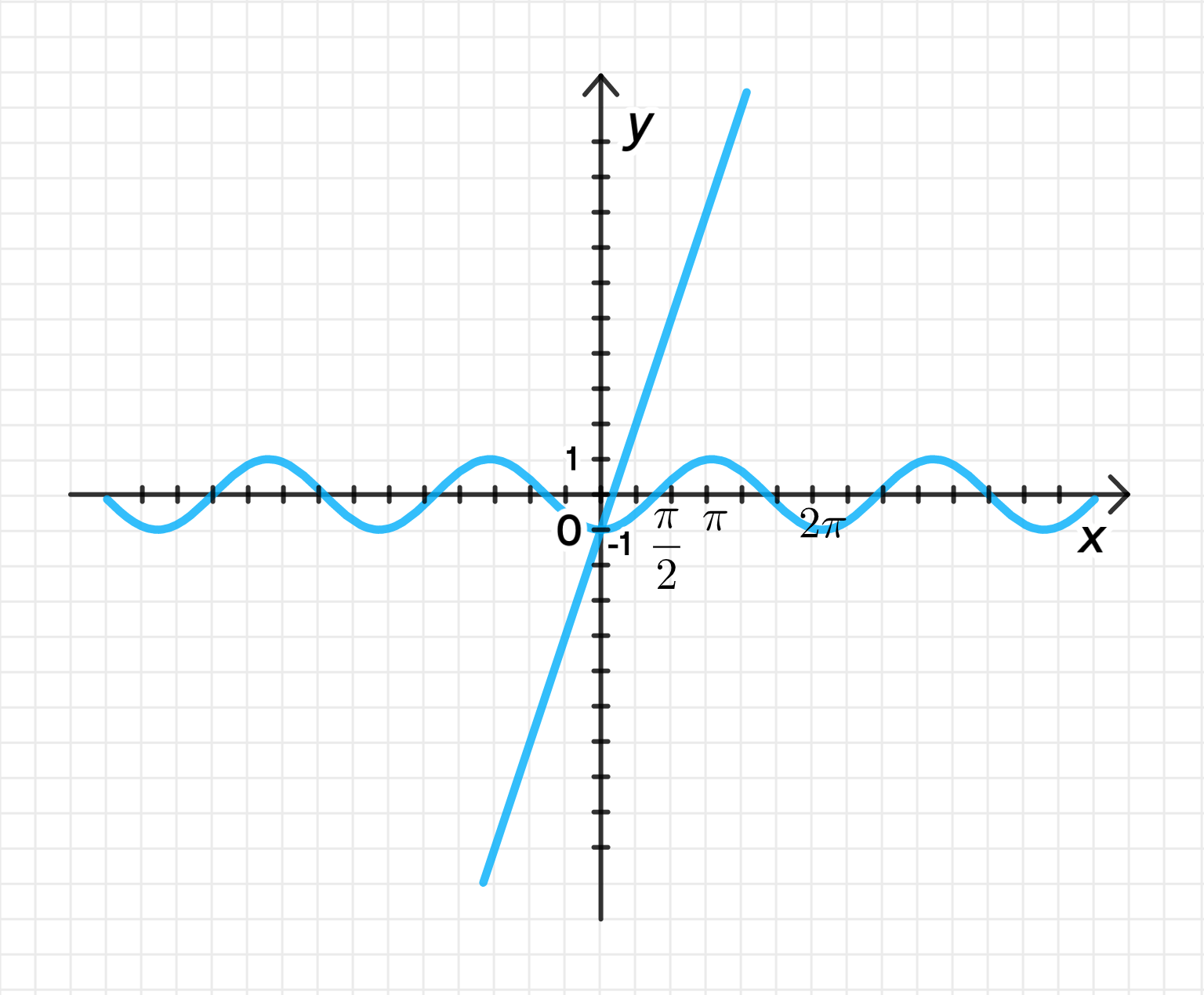
б) $-\cos x = 3x — 1$

Преобразуем уравнение:
Для удобства решим это уравнение, преобразовав его:

$$\cos x = 1 — 3x.$$

Теперь у нас есть уравнение, в котором синусоида $\cos x$ должна равняться прямой $1 — 3x$.

Анализ функции:

• $y = \cos x$ — уравнение синусоиды.
• $y = 1 — 3x$ — уравнение прямой с угловым коэффициентом $-3$ и сдвигом по оси $y$ на 1.

Построение таблицы значений:
Для определения точек пересечения можно составить таблицу значений:

Мы видим, что при $x = 0$, обе функции принимают значение $y = 1$, что означает, что функции пересекаются в точке $x = 0$.

Графики функций:

Ответ:
Пересечение происходит при $x = 0$.

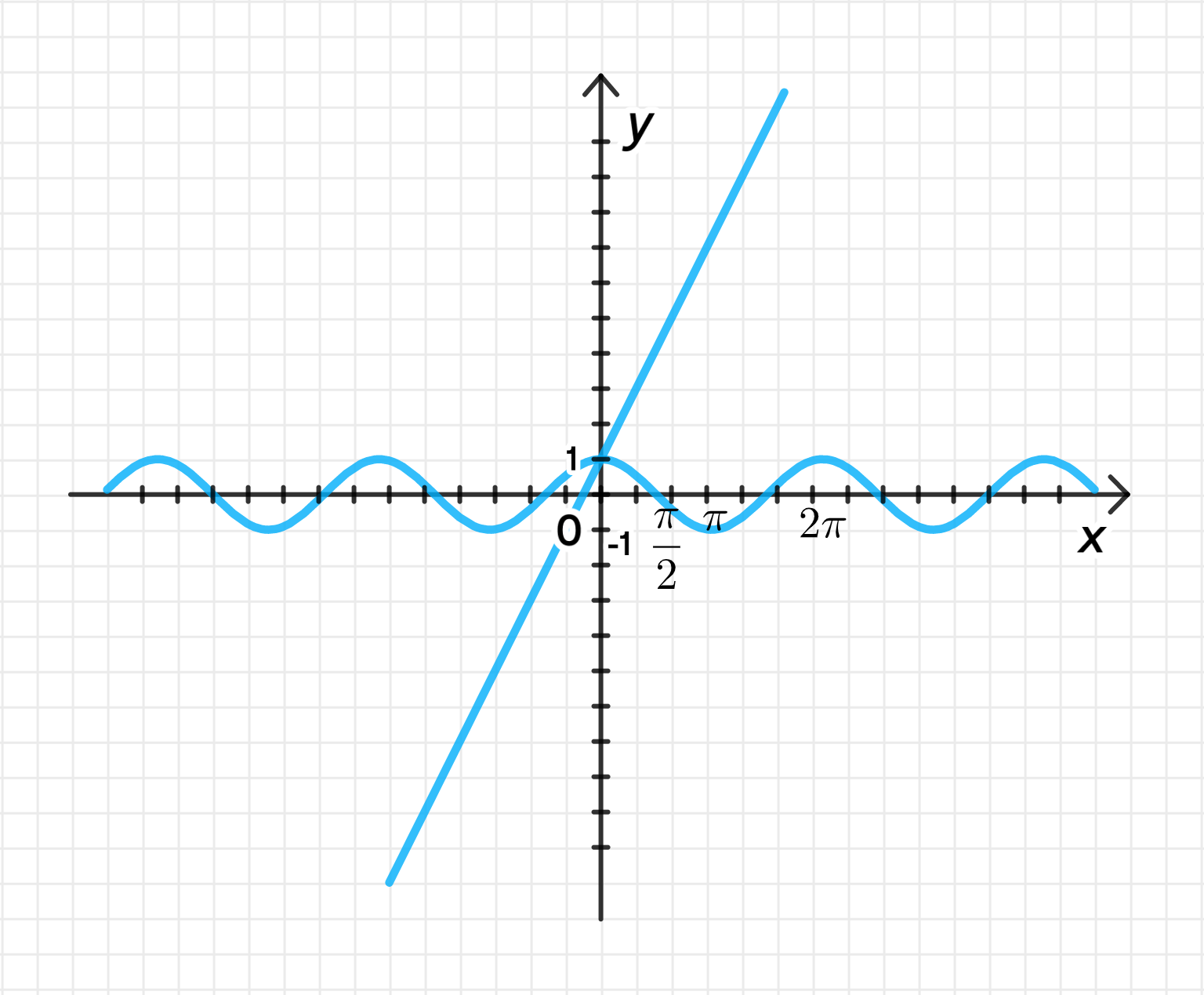
в) $\cos x = 2x + 1$

Преобразуем уравнение:

$$\cos x = 2x + 1.$$

Это уравнение связывает синусоиду с прямой.

Анализ функции:

• $y = \cos x$ — уравнение синусоиды.
• $y = 2x + 1$ — уравнение прямой с угловым коэффициентом 2 и сдвигом по оси $y$ на 1.

Построение таблицы значений:
Для удобства составим таблицу значений:

Мы видим, что при $x = 0$, обе функции равны 1, и это точка пересечения.

Графики функций:

Ответ:
Пересечение происходит при $x = 0$.

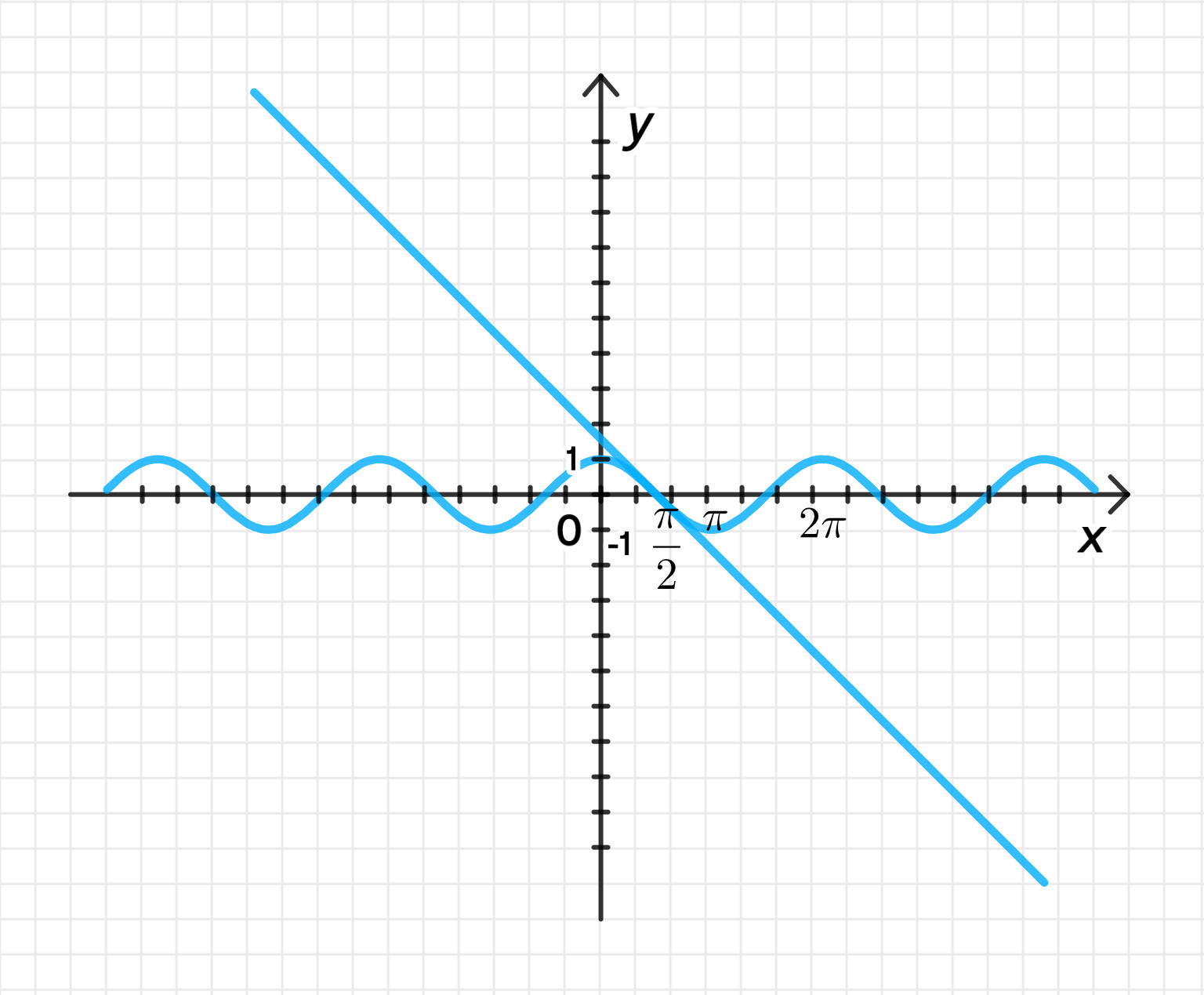
г) $\cos x = -x + \frac{\pi}{2}$

Преобразуем уравнение:

$$\cos x = -x + \frac{\pi}{2}.$$

В данном уравнении синусоида пересекается с прямой, которая имеет угловой коэффициент $-1$ и сдвиг по оси $y$ на $\frac{\pi}{2}$.

Анализ функции:

• $y = \cos x$ — уравнение синусоиды.
• $y = -x + \frac{\pi}{2}$ — уравнение прямой с угловым коэффициентом $-1$ и сдвигом по оси $y$ на $\frac{\pi}{2}$.

Построение таблицы значений:
Для нахождения точек пересечения составим таблицу значений:

Мы видим, что при $x = \frac{\pi}{2}$ обе функции принимают значение $0$.

Графики функций:

Ответ:
Пересечение происходит при $x = \frac{\pi}{2}$.

Итоговые ответы:

• Пересечение при $x = -\frac{\pi}{2}$.
• Пересечение при $x = 0$.
• Пересечение при $x = 0$.
• Пересечение при $x = \frac{\pi}{2}$.