Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 16.48 Профильный Уровень Мордкович — Подробные Ответы
а) ;
б) ;
в) ;
г)
а) ;
— уравнение синусоиды;
— уравнение ветви параболы:
Графики функций:
Ответ: .
б) ;
— уравнение синусоиды;
— уравнение ветви параболы:
Графики функций:
Ответ: .
в) ;
— уравнение синусоиды;
— уравнение параболы:
Графики функций:
Ответ: .
г) ;
— уравнение синусоиды;
— уравнение модуля:
Графики функций:
Ответ: .
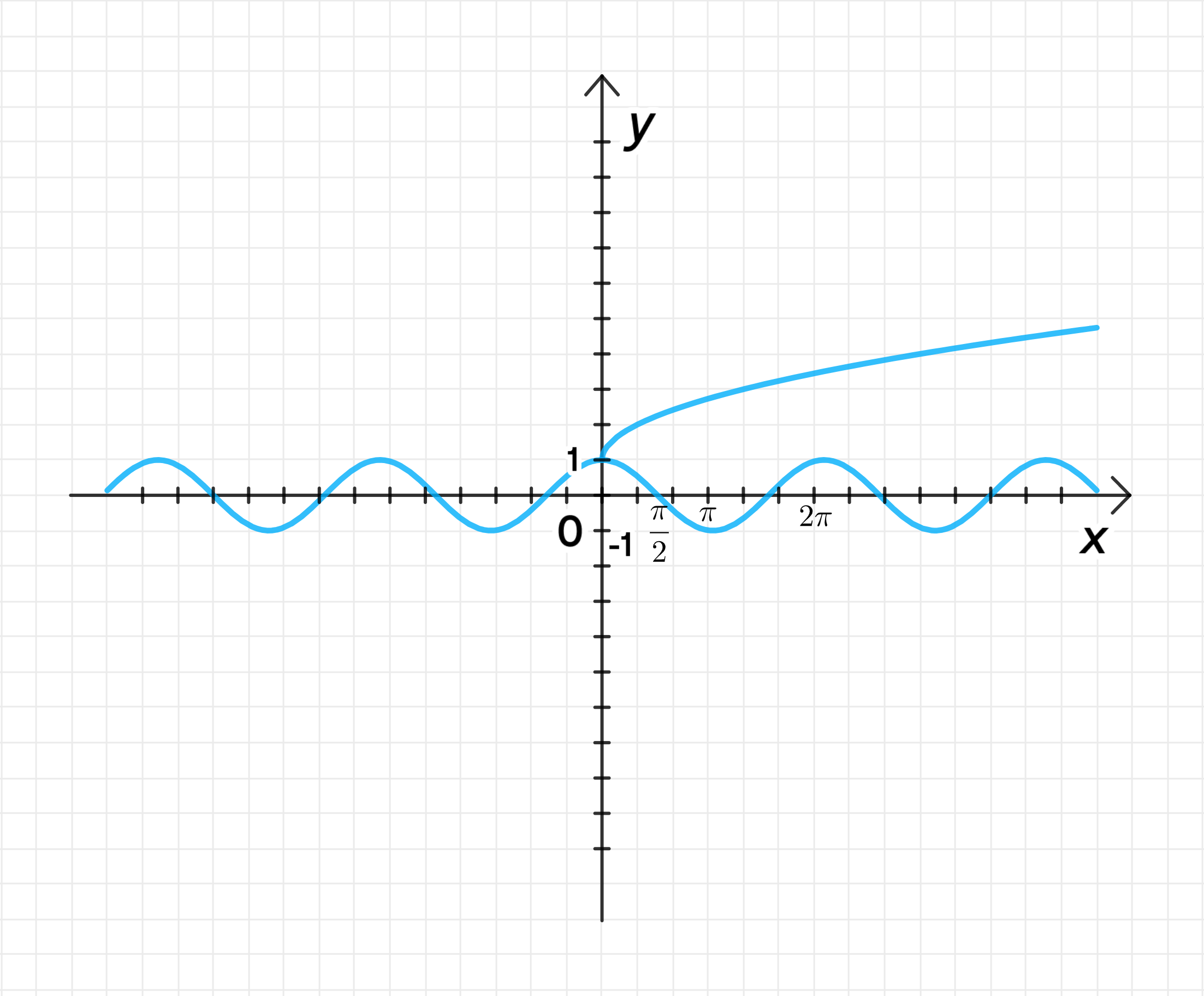
а) Уравнение:
Шаг 1: Исследование функций
Функция :
- Это стандартное уравнение синусоиды, которая колеблется между значениями -1 и 1 с периодом . То есть, она будет повторяться каждые единиц.
- График функции будет выглядеть как волна, которая достигает максимума в точке , затем спускается до -1, а затем снова возвращается к 1.
Функция :
- Это уравнение ветви параболы. Парабола начинает своё движение от и идёт вправо, поскольку определено только для . В точке значение функции будет равно 1. Как только увеличивается, значение функции будет расти, но всегда оставаться больше или равно 1.
Шаг 2: Таблица значений
Для того чтобы найти точку пересечения, нужно рассчитать значения функций в нескольких точках:
При обе функции принимают значение 1, то есть это точка пересечения.
При , и , значения функции и уже не совпадают.
Шаг 3: Графики функций
Ответ:
Пересечение происходит при .
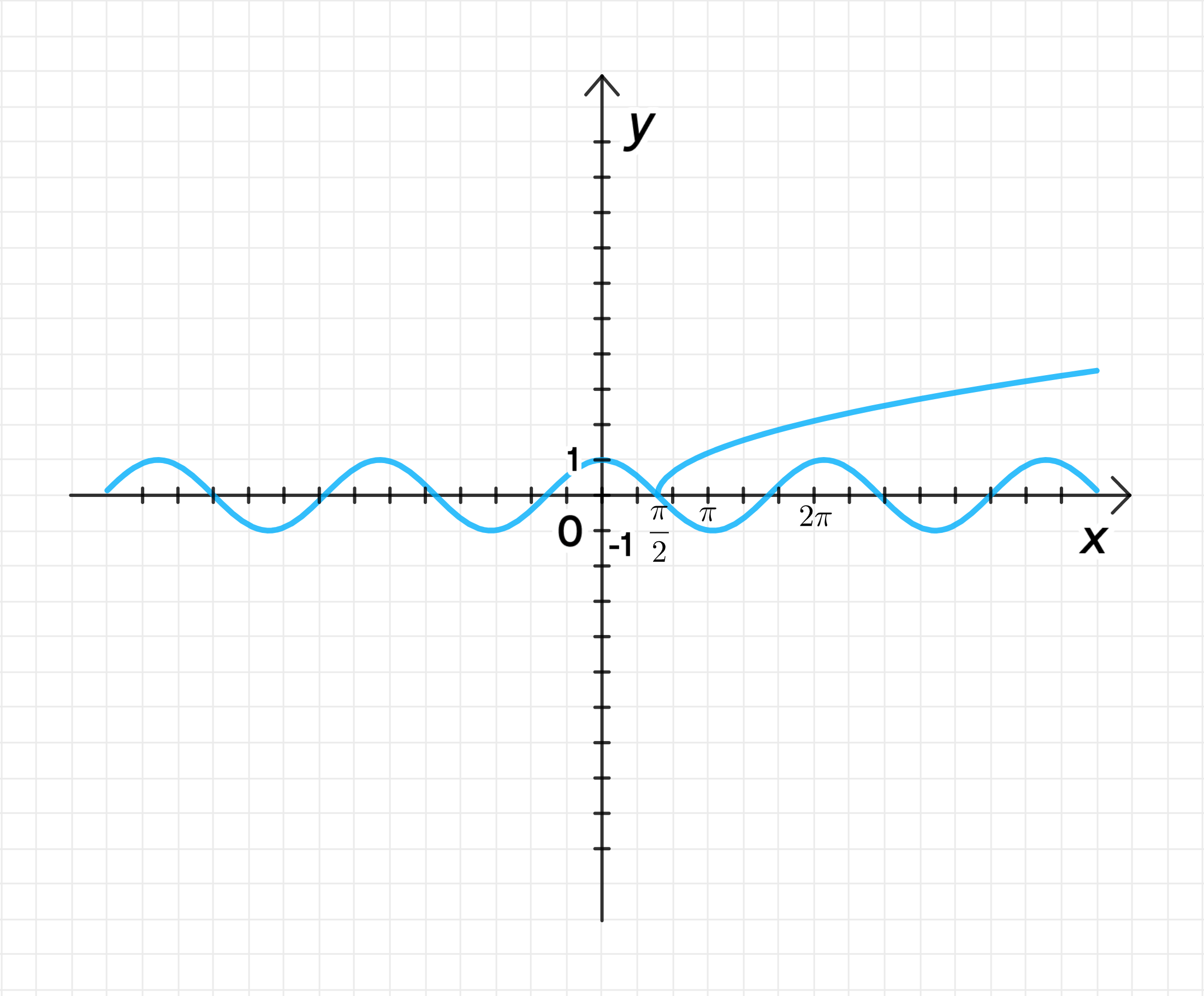
б) Уравнение:
Шаг 1: Исследование функций
Функция :
- Это стандартная синусоида, которая колеблется между -1 и 1 с периодом .
Функция :
- Это уравнение ветви параболы, но сдвиг по оси на . Эта функция определена для , так как значение под корнем должно быть неотрицательным.
- При , функция принимает значение 0, и с увеличением , значение функции будет возрастать.
Шаг 2: Таблица значений
Рассчитаем значения функций при и :
При , обе функции равны 0, что означает, что это точка пересечения.
Шаг 3: Графики функций
Ответ:
Пересечение происходит при .
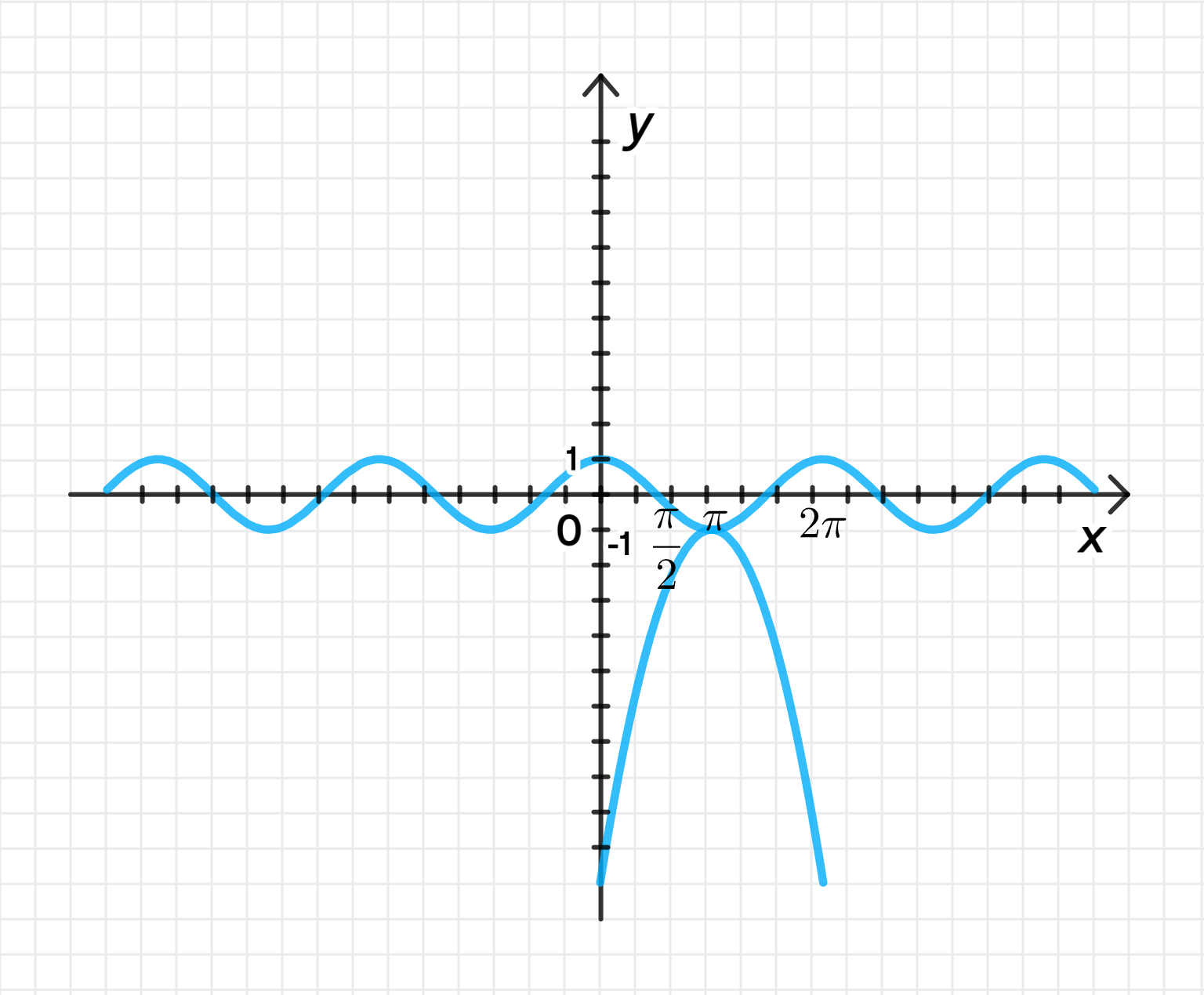
в) Уравнение:
Шаг 1: Исследование функций
Функция :
- Это стандартная синусоида, которая колеблется между -1 и 1 с периодом .
Функция :
- Это уравнение параболы, открывающейся вниз, с вершиной в точке , . Парабола будет уменьшаться на обеих сторонах от вершины.
Шаг 2: Таблица значений
Рассчитаем значения функций при и :
При , обе функции равны -1, что означает, что это точка пересечения.
Шаг 3: Графики функций
Ответ:
Пересечение происходит при .
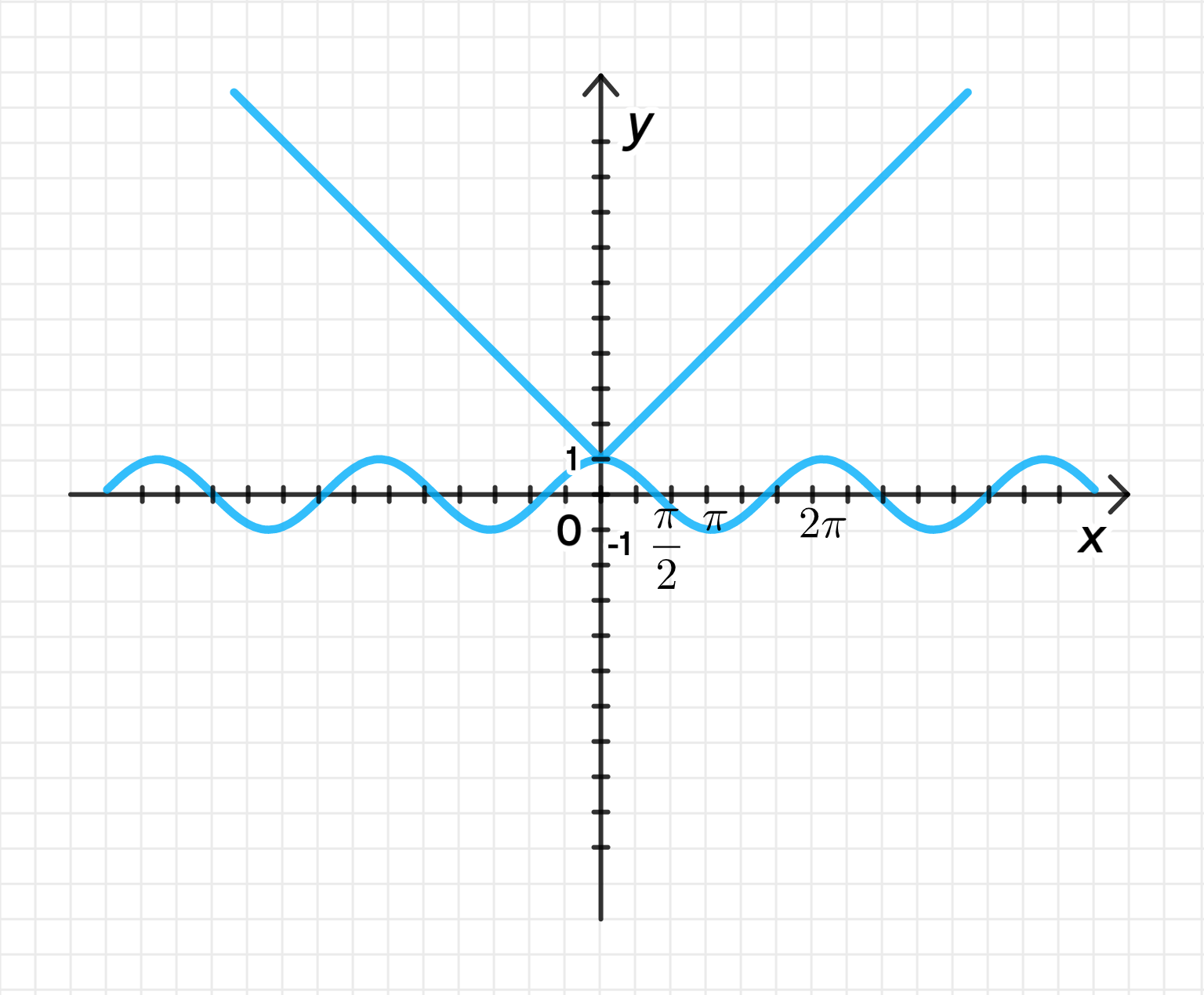
г) Уравнение:
Шаг 1: Исследование функций
Функция :
- Это стандартная синусоида, которая колеблется между -1 и 1 с периодом .
Функция :
- Это уравнение модуля, которое представляет собой «V»-образную фигуру, где на значение равно 1, а с увеличением значение функции растёт.
Шаг 2: Таблица значений
Рассчитаем значения функций при и :
При , обе функции равны 1, что означает, что это точка пересечения.
Шаг 3: Графики функций
Ответ:
Пересечение происходит при .
Итоговые ответы:
- Пересечение при для .
- Пересечение при для .
- Пересечение при для .
- Пересечение при для .