Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 16.49 Профильный Уровень Мордкович — Подробные Ответы
Сколько решений имеет система уравнений:
а)
б)
в)
г)
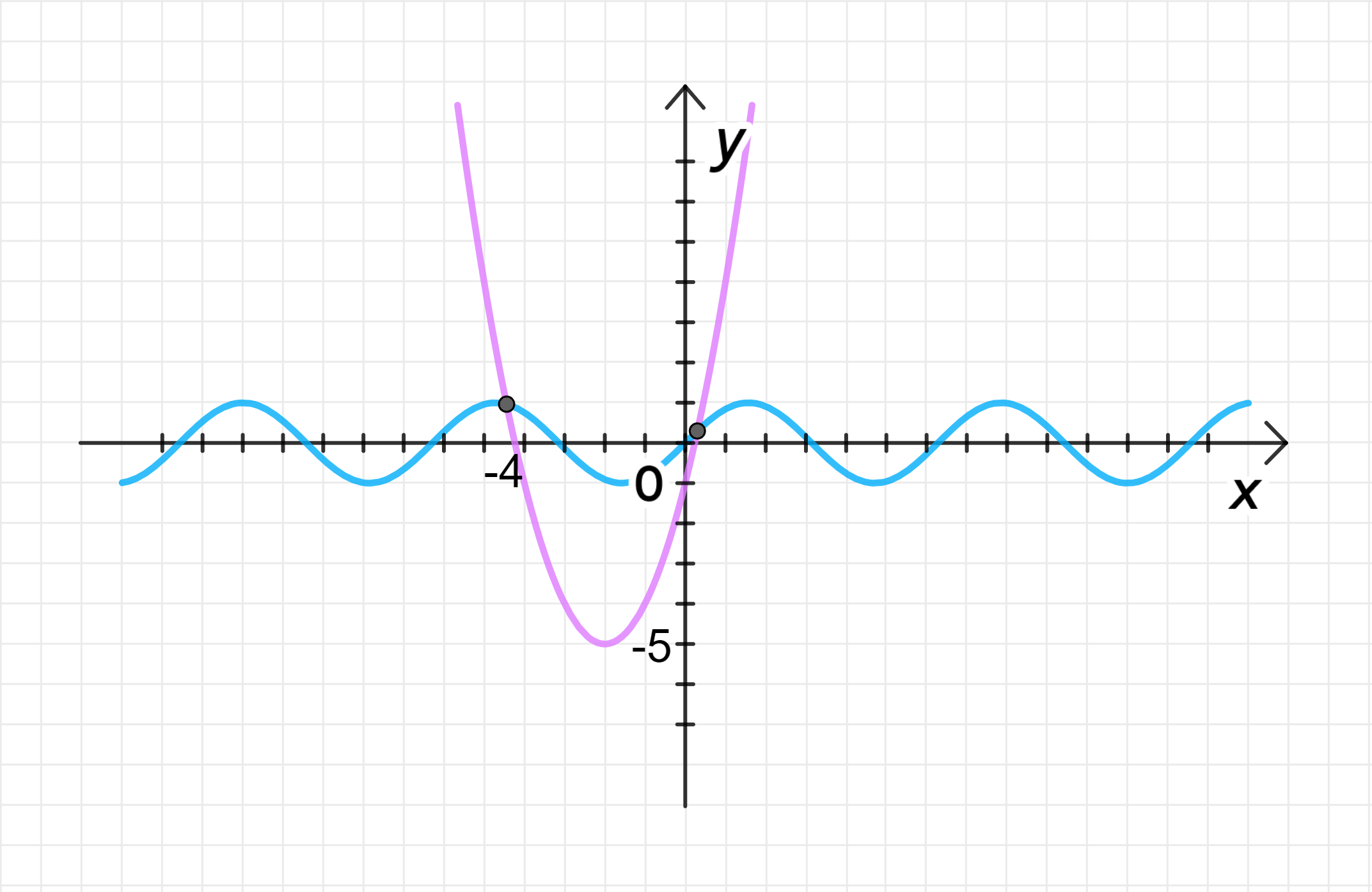
а)
Графики функций:
Ответ: 2 решения.
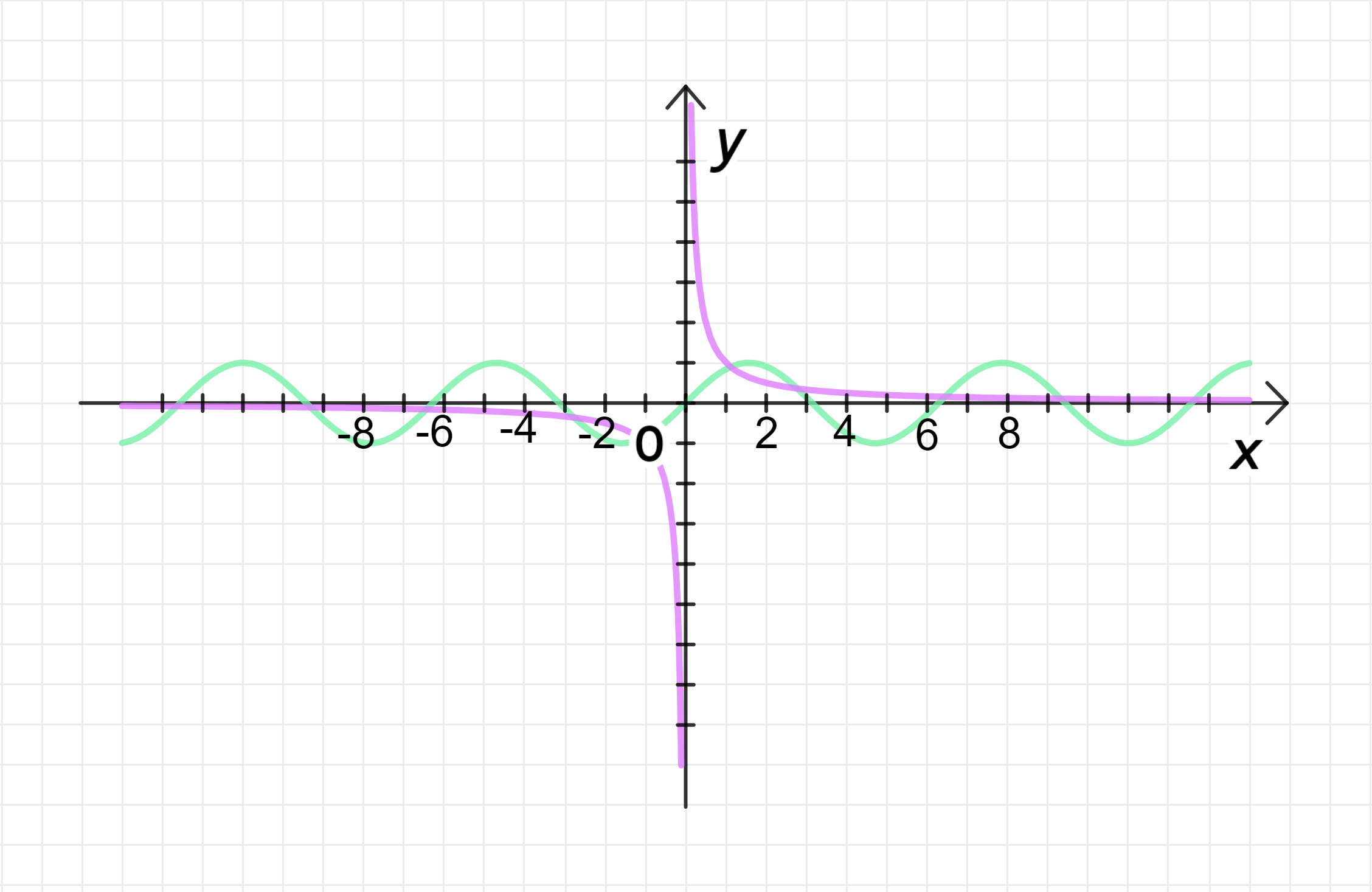
б)
Графики функций:
Ответ: бесконечно много решений.
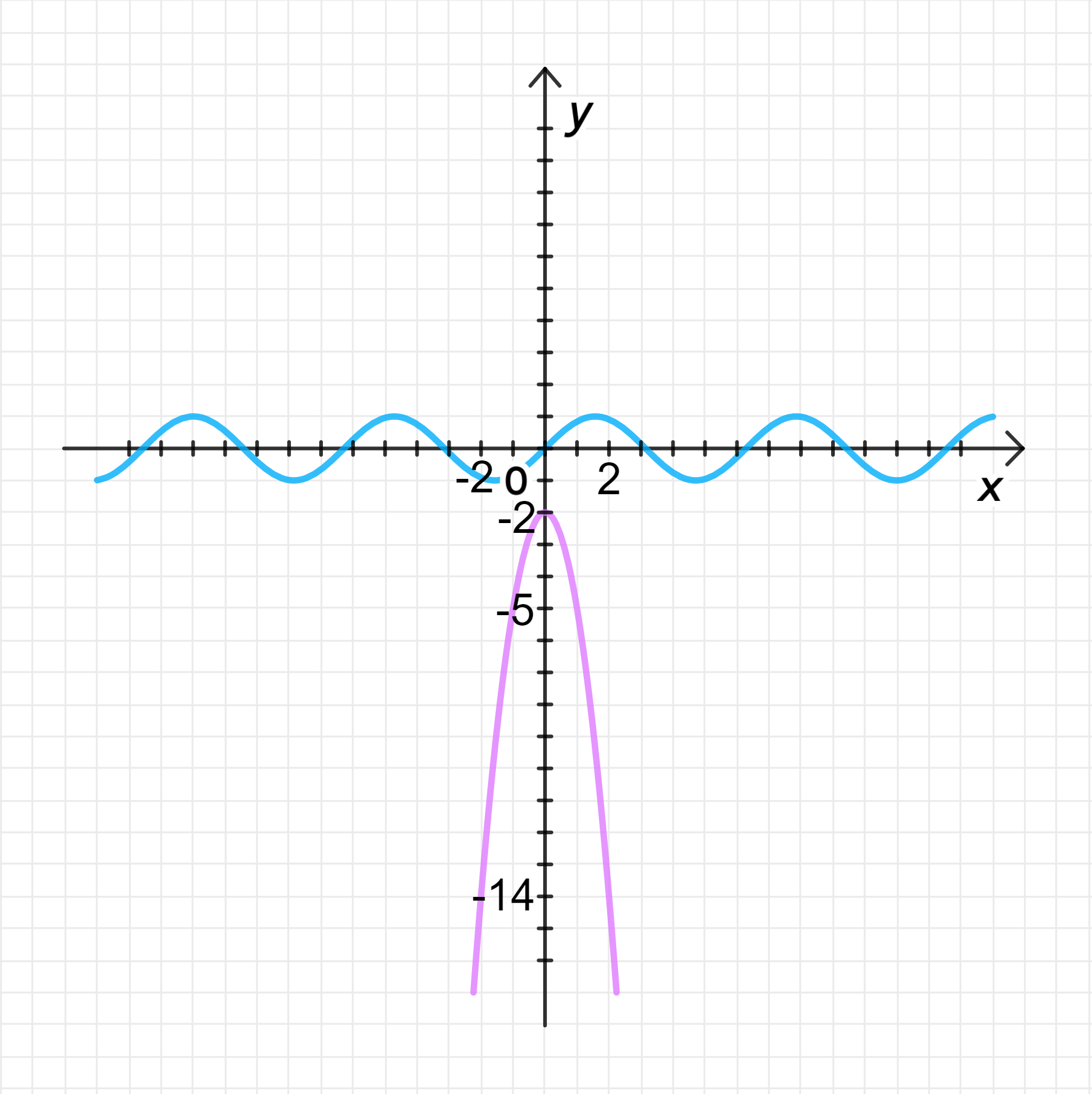
в)
Графики функций:
Ответ: 0 решений.
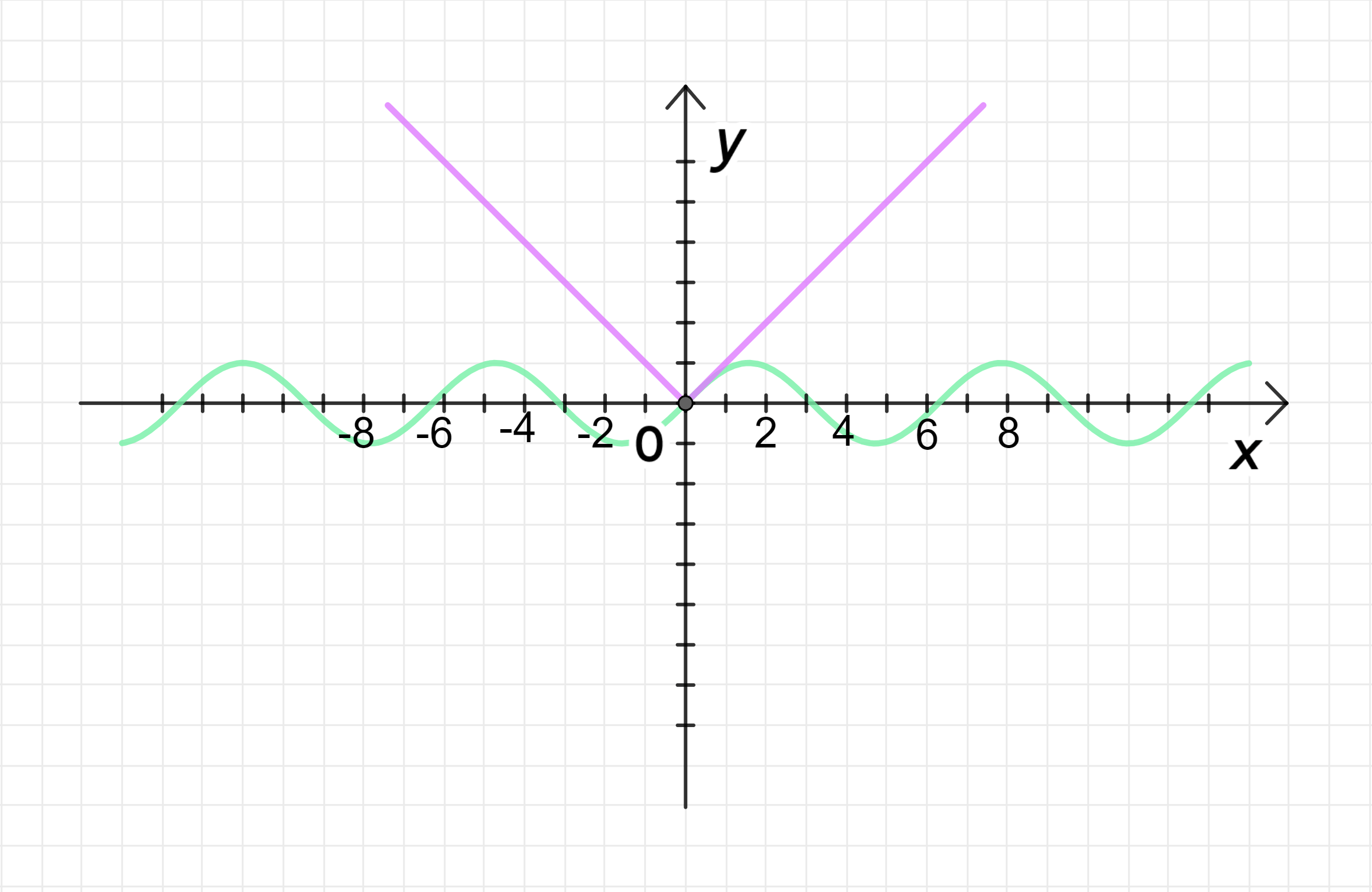
г)
Графики функций:
Ответ: 1 решение.
а) Уравнение:
Шаг 1: Исследуем каждую из функций.
Функция
- Это стандартное уравнение синусоиды, которая колеблется между -1 и 1. Период функции равен
2 π 2\pi - График этой функции будет волнообразным, начинаясь с
y = 0 y = 0 x = 0 x = 0 x = π 2 x = \frac{\pi}{2} x = π x = \pi 2 π 2\pi
Функция
- Это уравнение параболы с открытым вверх направлением, так как коэффициент при
x 2 x^2 - Мы можем найти вершину параболы, используя формулу для абсциссы вершины
x 0 = − b 2 a x_0 = -\frac{b}{2a} a = 1 a = 1 b = 4 b = 4 x 0 = − 4 2 ⋅ 1 = − 2. x_0 = -\frac{4}{2 \cdot 1} = -2. - Подставляем
x 0 = − 2 x_0 = -2 y 0 y_0 y 0 = ( − 2 ) 2 + 4 ( − 2 ) − 1 = 4 − 8 − 1 = − 5. y_0 = (-2)^2 + 4(-2) — 1 = 4 — 8 — 1 = -5. - Таким образом, вершина параболы находится в точке
( − 2 , − 5 ) (-2, -5)
Шаг 2: Таблица значений для обоих графиков.
Для анализа пересечений, посчитаем значения обеих функций в нескольких точках:
Шаг 3: Пересечения графиков.
Теперь нужно выяснить, на каких значениях
Обе функции равны при
Поскольку парабола
Ответ: 2 решения.
б) Уравнение:
Шаг 1: Исследуем функции.
Функция
- Как и раньше, это стандартная синусоида, которая колеблется между -1 и 1 с периодом
2 π 2\pi
Функция
- Это уравнение гиперболы, которая имеет асимптоты
x = 0 x = 0 y = 0 y = 0 - При
x = 0 x = 0 x → ∞ x \to \infty x → − ∞ x \to -\infty y y
Шаг 2: Таблица значений для обоих графиков.
Посчитаем значения для функции
Шаг 3: Пересечения графиков.
Здесь важно заметить, что гипербола
Ответ: бесконечно много решений.
в) Уравнение:
Шаг 1: Исследуем функции.
Функция
- Стандартная синусоида с периодом
2 π 2\pi
Функция
- Это парабола с открытием вниз, вершина которой находится в точке
( 0 , − 2 ) (0, -2) x 0 = 0 x_0 = 0 y 0 = − 2 y_0 = -2
Шаг 2: Таблица значений для обоих графиков.
Посчитаем значения функций:
Шаг 3: Пересечения графиков.
Мы видим, что значения функции синусоиды находятся в диапазоне от -1 до 1, в то время как значения параболы
Ответ: 0 решений.
г) Уравнение:
Шаг 1: Исследуем функции.
Функция
- Стандартная синусоида с амплитудой 1 и периодом
2 π 2\pi
Функция
- Это уравнение модуля, которое представляет собой V-образную кривую, которая имеет вершину в точке
x = 0 x = 0
Шаг 2: Таблица значений для обоих графиков.
Посчитаем значения для функции
| ( y = | x | ) |
Шаг 3: Пересечения графиков.
Графики пересекаются в точке
Ответ: 1 решение.
Итоговые ответы:
- 2 решения для
y = sin x y = \sin x y = x 2 + 4 x − 1 y = x^2 + 4x — 1 - Бесконечно много решений для
y = sin x y = \sin x y = 1 x y = \frac{1}{x} - 0 решений для
y = sin x y = \sin x y = − 3 x 2 − 2 y = -3x^2 — 2 - 1 решение для
y = sin x y = \sin x y = ∣ x ∣ y = |x|